Giải Toán lớp 5 VNEN bài 117: Em ôn lại những gì đã học

Giải bài tập Toán lớp 5

Giải Toán lớp 5 VNEN bài 117: Em ôn lại những gì đã học là lời giải Sách VNEN toán 5 tập 2 trang 139, 140 bao gồm chi tiết lời giải cho từng bài tập giúp các em học sinh củng cố, rèn kỹ năng giải Toán Chương 5 lớp 5. Mời các em học sinh tham khảo lời giải hay sau đây.

Bài 117: Em ôn lại những gì đã học

A. Hoạt động thực hành bài 117 Toán VNEN lớp 5
B. Hoạt động ứng dụng bài 117 Toán VNEN lớp 5
- Câu 1: Trang 140 toán VNEN lớp 5 tập 2
- Câu 2: Trang 140 toán VNEN lớp 5 tập 2

A. Hoạt động thực hành bài 117 Toán VNEN lớp 5

Câu 1: Trang 139 toán VNEN lớp 5 tập 2

Chơi trò chơi "đố ai tìm nhanh?"

a. Tìm $\frac{1}{2};\frac{1}{3};\frac{1}{5};\frac{1}{6};\frac{1}{10};\frac{1}{12}$ $\frac{1}{2};\frac{1}{3};\frac{1}{5};\frac{1}{6};\frac{1}{10};\frac{1}{12}$ của 60

b. Tìm 15%, 20%, 50%, 75% của 60

c. Tìm các số mà 60 chia hết cho số đó

Hướng dẫn giải:

a) Muốn tìm phân số của một số, ta lấy số đó nhân với phân spố

b) Muốn tìm phần trăm của một số, ta lấy số đó chia cho 100 rồi tiếp tục nhân với số phần trăm hoặc lấy số đó nhân với số phần trăm rồi chia cho 100

Đáp án

a.

a) $\dfrac{1}{2}$ $\dfrac{1}{2}$của 60 là $60 × \dfrac{1}{2}= 30$ $60 × \dfrac{1}{2}= 30$; $\dfrac{1}{3}$ $\dfrac{1}{3}$ của 60 là $60 × \dfrac{1}{3}= 20$ $60 × \dfrac{1}{3}= 20$;

$\dfrac{1}{5}$ $\dfrac{1}{5}$ của 60 là $60 × \dfrac{1}{5}= 12$ $60 × \dfrac{1}{5}= 12$; $\dfrac{1}{6}$ $\dfrac{1}{6}$ của 60 là $60 × \dfrac{1}{6}= 10$ $60 × \dfrac{1}{6}= 10$;

$\dfrac{1}{{10}}$ $\dfrac{1}{{10}}$ của 60 là $60 × \dfrac{1}{{10}}= 6$ $60 × \dfrac{1}{{10}}= 6$; $\dfrac{1}{{12}}$ $\dfrac{1}{{12}}$ của 60 là $60 × \dfrac{1}{{12}}= 5$ $60 × \dfrac{1}{{12}}= 5$.

b. 15% của 60 bằng 9; 20% của 60 bằng 12; 50% của 60 bằng 30; 75% của 60 bằng 45

c. Các số mà 60 chia hết cho số đó là: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.

Câu 2: Trang 139 toán VNEN lớp 5 tập 2

Tính:

a. $1\frac{5}{7}\times\frac{3}{4}$ $1\frac{5}{7}\times\frac{3}{4}$

b. $\frac{10}{11}:\ 1\frac{1}{3}$ $\frac{10}{11}:\ 1\frac{1}{3}$

c. 3,57 x 4,1 + 2,43 x 4,1

d. 3,42 : 0,75 x 8,4 - 6,8

Hướng dẫn giải:

a) Đổi hỗn số về dạng hỗn số rồi thực hiện phép nhân hai phân số.

Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

b) Đổi hỗn số về dạng hỗn số rồi thực hiện phép nhân chia phân số.

Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.

c) Áp dụng công thức nhân một tổng với một số: (a + b) × c = a × c + b × c

d) Biểu thức có các phép tính cộng, trừ, nhân, chia thì thực hiện phép tính nhân, chia trước, thực hiện phép tính cộng, trừ sau.

Đáp án

a) $1\dfrac{5}{7} \times \dfrac{3}{4} = \dfrac{{12}}{7} \times \dfrac{3}{4} = \dfrac{{12 \times 3}}{{7 \times 4}} = \dfrac{{4 \times 3 \times 3}}{{7 \times 4}} = \dfrac{9}{7}$ $1\dfrac{5}{7} \times \dfrac{3}{4} = \dfrac{{12}}{7} \times \dfrac{3}{4} = \dfrac{{12 \times 3}}{{7 \times 4}} = \dfrac{{4 \times 3 \times 3}}{{7 \times 4}} = \dfrac{9}{7}$

b) $\dfrac{{10}}{{11}}:1\dfrac{1}{3} = \dfrac{{10}}{{11}}:\dfrac{4}{3} = \dfrac{{10}}{{11}} \times \dfrac{3}{4} = \dfrac{{10 \times 3}}{{11 \times 4}} = \dfrac{{5 \times 2 \times 3}}{{11 \times 2 \times 2}} = \dfrac{{15}}{{22}}$ $\dfrac{{10}}{{11}}:1\dfrac{1}{3} = \dfrac{{10}}{{11}}:\dfrac{4}{3} = \dfrac{{10}}{{11}} \times \dfrac{3}{4} = \dfrac{{10 \times 3}}{{11 \times 4}} = \dfrac{{5 \times 2 \times 3}}{{11 \times 2 \times 2}} = \dfrac{{15}}{{22}}$

c. 3,57 x 4,1 + 2,43 x 4,1

= (3,57 + 2,43) x 4,1

= 6 x 4,1

= 24,6

d. 3,42 : 0,57 x 8,4 - 6,8

= 6 x 8,4 - 6,8

= 50,4 - 6,8

= 43,6

Câu 3: Trang 139 toán VNEN lớp 5 tập 2

Tính bằng cách thuận tiện nhất:

a) $\dfrac{{21}}{{11}} \times \dfrac{{22}}{{17}} \times \dfrac{{68}}{{63}}$ $\dfrac{{21}}{{11}} \times \dfrac{{22}}{{17}} \times \dfrac{{68}}{{63}}$

b) $\dfrac{5}{{14}} \times \dfrac{7}{{13}} \times \dfrac{{26}}{{25}}$ $\dfrac{5}{{14}} \times \dfrac{7}{{13}} \times \dfrac{{26}}{{25}}$

Hướng dẫn giải

- Muốn nhân nhiều phân số ta lấy các tử số nhân với nhau, các mẫu số nhân với nhau.

- Tách tử số và mẫu số thành tích của các thừa số, sau đó chia nhẩm tích ở tử số và mẫu số cho các thừa số chung.

Đáp án

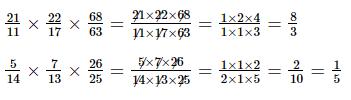
Câu 4: Trang 139 toán VNEN lớp 5 tập 2

Một bể bơi dạng hình hộp chữ nhật có chiều dài 22,5m, chiều rộng 19,2m. Nếu bể chứa 414,72m³ thì mực nước trong bể lên đến $\frac{4}{5}$ $\frac{4}{5}$ chiều cao của bể. Hỏi chiều cao của bể là bao nhiêu mét?

Hướng dẫn giải

- Tính diện tích đáy bể = chiều dài × chiều rộng.

- Tính chiều cao mực nước trong bể = thể tích nước trong bể : diện tích đáy bể.

- Tính chiều cao của bể = chiều cao mực nước trong bể : 4 × 5.

Đáp án

Theo công thức tính thể tích hình hộp chữ nhật ta có: V = a x b x c

Vậy chiều cao của mực nước trong bể là:

414,72 : (22,5 x 19,2) = 0,96 (m)

Vậy chiều cao của bể nước là:

(0,96 : 4 ) x 5 = 1,2 (m)

Đáp số: 1,2m

Câu 5: Trang 139 toán VNEN lớp 5 tập 2

Một con thuyền đi với vận tốc 7,2km/giờ khi nước lặng, vận tốc của dòng nước là 1,6km/giờ.

a. Nếu thuyền đi xuôi dòng thì sau bao 3,5 giờ sẽ đi được bao nhiêu ki-lô-mét?

b. Nếu thuyền đi ngược dòng thì cần bao nhiêu thời gian để đi được quãng đường như khi xuôi dòng trong 3,5 giờ?

Hướng dẫn giải

Áp dụng các công thức:

- Vận tốc xuôi dòng = vận tốc khi nước lặng + vận tốc dòng nước.

- Vận tốc ngược dòng = vận tốc khi nước lặng – vận tốc dòng nước.

- Quãng đường = vận tốc xuôi dòng × thời gian đi xuôi dòng = vận tốc ngược dòng × thời gian đi ngược dòng.

Đáp án

a. Vận tốc của thuyền máy khi xuôi dòng là:

7,2 + 1,6 = 8,8 (km/giờ)

Vậy trong 3,5 giờ thuyền máy đi được số km là:

8,8 x 3,5 = 30,8 (km)

b. Vận tốc của thuyền máy khi đi ngược dòng là:

7,2 - 1,6 = 5,6 (km/giờ)

Vậy, để đi được 30,8km thì thuyền máy đi trong thời gian là:

30,8 : 5,6 = 5,5 (giờ)

Đáp số: a. 30,8 km

b. 5,5 giờ

Câu 6: Trang 139 toán VNEN lớp 5 tập 2

Tìm x: 8,75 x X + 1,25 x X = 20

Hướng dẫn giải:

Áp dụng công thức nhân một số với một tổng:

a × c + b × c = (a + b) × c

Đáp án

8,75 x X + 1,25 x X = 20

(8,75 + 1,25) x X = 20

10 x X = 20

X = 20 : 10

X = 2

=>Vậy x = 2

B. Hoạt động ứng dụng bài 117 Toán VNEN lớp 5

Câu 1: Trang 140 toán VNEN lớp 5 tập 2

Một người đi xe máy từ Nam Định về Hà Nội với vận tốc 40km/giờ, sau 1 giờ 30 phút người đó gặp cột cây ghi Hà Nội 30km. Hỏi người đó đã đi được bao nhiêu km và phải đi bao nhiêu thời gian với cùng vận tốc trên thì về đến Hà Nội.

Hướng dẫn giải

Áp dụng các công thức:

+) Quãng đường = Vận tốc × Thời gian.

+) Thời gian = Quãng đường : Vận tốc.

Đáp án

Đổi: 1 giờ 30 phút = 1,5 giờ

Sau 1 giờ 30 phút người đó đã đi được số km là:

40 x 1,5 = 60 (km)

Vậy để đi 30 km còn lại, người đó phải mất số thời gian là:

30 : 40 = 0,75 (giờ) = 45 phút

Đáp số: người đó đi được: 60km

Thời gian người đó cần đi 45 phút