Toán 10 Bài 3: Dấu của nhị thức bậc nhất

Toán 10 Bài 3: Dấu của nhị thức bậc nhất được VnDoc biên soạn bao gồm hướng dẫn lý thuyết và hướng dẫn giải cho từng bài tập sách giáo khoa và sách bài tập giúp các bạn học sinh luyện tập và hiểu rõ về cách xét dấu các đa thức bậc nhất, cách giải các bất phương trình, .... Qua đó giúp các bạn học sinh ôn tập, củng cố và rèn luyện thêm kiến thức đã học trong chương trình Toán 10, Mời các bạn học sinh và quý thầy cô cùng tham khảo chi tiết.

Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

A. Lí thuyết Dấu của nhị thức bậc nhất

1. Nhị thức bậc nhất

- Nhị thức bậc nhất đối với x là biểu thức có dạng \(f\left( x \right)=ax+b\) trong đó a, b là hai số đã cho, \(a\ne 0\)

Định lí: Nhị thức \(f\left( x \right)=ax+b,a\ne 0\) ta có:

• Cùng dấu với hệ số a khi x lấy các giá trị trong khoảng \(\left( -\frac{b}{a},+\infty \right)\)
• Trái dấu với hệ số a khi lấy các giá trị trong khoảng \(\left( -\infty ,-\frac{b}{a} \right)\)

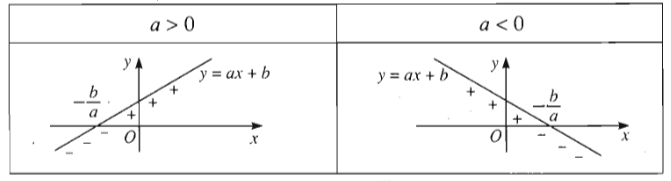
Bảng tóm tắt dấu:

Minh họa bằng đồ thị:

2. Bất phương trình chứa dấu giá trị tuyệt đối

• \(\left| f\left( x \right) \right|\le a\Leftrightarrow -a\le f\left( x \right)\le a\)
• \(\left| f\left( x \right) \right|\ge a\Leftrightarrow \left[ \begin{matrix} f\left( x \right)\le -a \\ f\left( x \right)\ge a \\ \end{matrix} \right.\)

3. Dấu nhị thức bậc nhất trên một miền

• \(f\left( x \right)\ge 0,\forall x\Leftrightarrow \left\{ \begin{matrix} a=0 \\ b\ge 0 \\ \end{matrix} \right.\)
• \(f\left( x \right)\le 0,\forall x\Leftrightarrow \left\{ \begin{matrix} a=0 \\ b\le 0 \\ \end{matrix} \right.\)
• \(f\left( x \right)\ge 0,\forall x\ge \beta \Leftrightarrow \left\{ \begin{matrix} a\ge 0 \\ f\left( \beta \right)\ge 0 \\ \end{matrix} \right.\)
• \(f\left( x \right)\le 0,\forall x\ge \beta \Leftrightarrow \left\{ \begin{matrix} a\le 0 \\ f\left( \beta \right)\le 0 \\ \end{matrix} \right.\)
• \(f\left( x \right)\ge 0,\forall x\le \beta \Leftrightarrow \left\{ \begin{matrix} a\le 0 \\ f\left( \beta \right)\ge 0 \\ \end{matrix} \right.\)
• \(f\left( x \right)\le 0,\forall x\le \beta \Leftrightarrow \left\{ \begin{matrix} a\ge 0 \\ f\left( \beta \right)\le 0 \\ \end{matrix} \right.\)
• \(f\left( x \right)\ge 0,\forall x\in \left( \alpha ,\beta \right)\Leftrightarrow \left\{ \begin{matrix} f\left( \alpha \right)\ge 0 \\ f\left( \beta \right)\ge 0 \\ \end{matrix} \right.\)
• \(f\left( x \right)\le 0,\forall x\in \left( \alpha ,\beta \right)\Leftrightarrow \left\{ \begin{matrix} f\left( \alpha \right)\le 0 \\ f\left( \beta \right)\le 0 \\ \end{matrix} \right.\)

Ví dụ: Giải bất phương trình_{\(\frac{\left( 2x-1 \right)\left( 3-x \right)}{{{x}^{2}}-5x+4}<0\)}

Hướng dẫn giải

\(\frac{\left( 2x-1 \right)\left( 3-x \right)}{{{x}^{2}}-5x+4}=\frac{\left( 2x-1 \right)\left( 3-x \right)}{\left( x-1 \right)\left( x-4 \right)}<0\)

Ta có:

\(\begin{align} & 2x-1=0\Leftrightarrow x=\frac{1}{2} \\ & 3-x=0\Leftrightarrow x=3 \\ & x-1=0\Leftrightarrow x=1 \\ & x-4=0\Leftrightarrow x=4 \\ \end{align}\)

Lập bảng xét dấu:

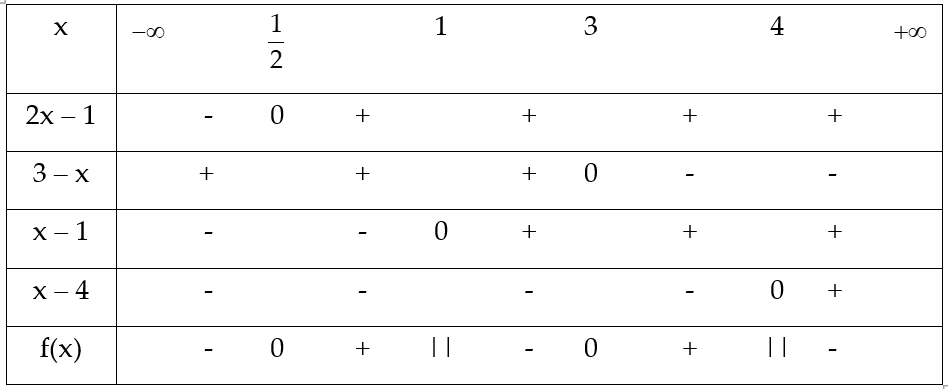
Vật bất phương trình có tập nghiệm \(S=\left( -\infty ,\frac{1}{2} \right)\cup \left( 1,3 \right)\cup \left( 4,+\infty \right)\)

B. Giải SGK Toán 10 Bài 3

Trong Sách giáo khoa Toán lớp 10, các bạn học sinh chắc hẳn sẽ gặp những bài toán khó, phải tìm cách giải quyết. Hiểu được điều này, VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho các bài tập trong Sách giáo khoa Toán lớp 10. Mời các bạn học sinh tham khảo:

• Giải bài tập trang 94 SGK Đại số 10: Dấu của nhị thức bậc nhất

C. Giải SBT Toán 10 Bài 3

Sách bài tập Toán 10 tổng hợp các bài Toán từ cơ bản tới nâng cao, đi kèm với đó là đáp án. Tuy nhiên, nhiều đáp án không được giải chi tiết khiến cho các bạn học sinh gặp nhiều khó khăn khi tiếp xúc với dạng bài mới. VnDoc đã tổng hợp và gửi tới các bạn học sinh lời giải và đáp án chi tiết cho từng dạng bài tập trong Sách bài tập để các bạn có thể nắm vững, hiểu rõ hơn về dạng bài tập này. Mời các bạn học sinh tham khảo:

• Giải bài tập Toán 10 SBT bài 3 chương 4

D. Bài tập trắc nghiệm Toán 10

Để ôn tập lại kiến thức cũng như rèn luyện nâng cao hơn về bài tập của phần Bất phương trình này, VnDoc xin gửi tới các bạn học sinh Tài liệu Bài tập Dấu nhị thức bậc nhất do VnDoc biên soạn. Qua đó sẽ giúp các bạn học sinh hiểu sâu hơn và nắm rõ hơn lý thuyết cũng như bài tập của bài học này. Mời các bạn học sinh tham khảo:

• Bài tập trắc nghiệm: Dấu của nhị thức bậc nhất

------------------------------------

Trên đây VnDoc đã giới thiệu tới các bạn bài Toán 10 Bài 3: Dấu của nhị thức bậc nhất. Hy vọng với tài liệu này các bạn học sinh sẽ nắm chắc kiến thức vận dụng tốt vào giải bài tập từ đó học tốt môn Toán lớp 10. Chúc các bạn học tốt và nhớ thường xuyên tương tác để cập nhật được nhiều bài tập hay bổ ích nhé!

Ngoài ra, VnDoc giới thiệu thêm tới bạn đọc tham khảo một vài tài liệu liên quan tới chương trình lớp 10: Ngữ Văn 10, Tiếng Anh lớp 10, Vật lý lớp 10,...