Toán lớp 4 trang 134: Luyện tập phép nhân phân số

Giải bài tập Toán lớp 4

Giải bài tập trang 134 SGK Toán 4: Luyện tập phép nhân phân số bao gồm đáp án và hướng dẫn giải chi tiết giúp các em học sinh ôn tập lại những kiến thức căn bản của phép nhân phân số, luyện tập cách thực hiện phép nhân 2, 3 phân số. Sau đây mời các em cùng tham khảo lời giải chi tiết.

Hướng dẫn giải bài Luyện tập phép nhân phân số – SGK toán 4 (bài 1, 2, 3, SGK Toán lớp 4 trang 134)

Giải Toán lớp 4 trang 134 Bài 1

a) Viết tiếp vào chỗ chấm:

+) Nhận xét: $\displaystyle{2 \over 3} \times {4 \over 5} = \;...$ $\displaystyle{2 \over 3} \times {4 \over 5} = \;...$; $\displaystyle{4 \over 5} \times {2 \over 3} =\; ...$ $\displaystyle{4 \over 5} \times {2 \over 3} =\; ...$

Vậy: $\displaystyle{2 \over 3} \times {4 \over 5} \cdots {4 \over 5} \times {2 \over 3}$ $\displaystyle{2 \over 3} \times {4 \over 5} \cdots {4 \over 5} \times {2 \over 3}$.

Tính chất giao hoán: Khi đổi chỗ các phân số trong một tích thì tích của chúng không thay đổi.

+) Nhận xét: $\displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} = \cdots$ $\displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} = \cdots$

$\displaystyle{1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right) = \cdots$ $\displaystyle{1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right) = \cdots$

Vậy: $\displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} \cdots {1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right)$ $\displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} \cdots {1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right)$

Tính chất kết hợp: Khi nhân một tích hai phân số với phân số thứ ba, ta có thể nhân phân số thứ nhất với tích của phân số thứ hai và phân số thứ ba.

+) Nhận xét: $\displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} = \cdots$ $\displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} = \cdots$ ;

$\displaystyle{1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4} = \cdots$ $\displaystyle{1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4} = \cdots$

Vậy: $\displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} \cdots {1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4}$ $\displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} \cdots {1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4}$

Khi nhân một tổng hai phân số với phân số thứ ba, ta có thể nhân từng phân số của tổng với phân số thứ ba rồi cộng các kết quả lại.

b) Tính bằng hai cách:

$\displaystyle{3 \over {22}} \times {3 \over {11}} \times 22;$ $\displaystyle{3 \over {22}} \times {3 \over {11}} \times 22;$

$\displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5};$ $\displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5};$

$\displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5}.$ $\displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5}.$

Đáp án

Phương pháp giải:

Áp dụng các tính chất giao hoán, kết hợp, nhân một tổng với một số để tính giá trị các biểu thức đã cho.

Đáp án

a) +) $\displaystyle \displaystyle{2 \over 3} \times {4 \over 5} = {{2 \times 4} \over {3 \times 5}} = {8 \over {15}}$ $\displaystyle \displaystyle{2 \over 3} \times {4 \over 5} = {{2 \times 4} \over {3 \times 5}} = {8 \over {15}}$

$\displaystyle \displaystyle{4 \over 5} \times {2 \over 3} = {{4 \times 2} \over {5 \times 3}} = {8 \over {15}}$ $\displaystyle \displaystyle{4 \over 5} \times {2 \over 3} = {{4 \times 2} \over {5 \times 3}} = {8 \over {15}}$

Vậy: $\displaystyle \displaystyle{2 \over 3} \times {4 \over 5}= {4 \over 5} \times {2 \over 3}$ $\displaystyle \displaystyle{2 \over 3} \times {4 \over 5}= {4 \over 5} \times {2 \over 3}$

+) $\displaystyle \displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} = {2 \over {15}} \times {3 \over 4} = {{2 \times 3} \over {15 \times 4}}$ $\displaystyle \displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} = {2 \over {15}} \times {3 \over 4} = {{2 \times 3} \over {15 \times 4}}$

$\displaystyle \displaystyle= {{2 \times 3} \over {3 \times 5 \times 2 \times 2}} = {1 \over {10}}$ $\displaystyle \displaystyle= {{2 \times 3} \over {3 \times 5 \times 2 \times 2}} = {1 \over {10}}$

$\displaystyle \displaystyle{1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right) = {1 \over 3} \times {{2 \times 3} \over {5 \times 4}}$ $\displaystyle \displaystyle{1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right) = {1 \over 3} \times {{2 \times 3} \over {5 \times 4}}$

$\displaystyle \displaystyle= {{1 \times 2 \times 3} \over {3 \times 5 \times 2 \times 2}} = {1 \over {10}}$ $\displaystyle \displaystyle= {{1 \times 2 \times 3} \over {3 \times 5 \times 2 \times 2}} = {1 \over {10}}$

Vậy: $\displaystyle \displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} = {1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right)$ $\displaystyle \displaystyle\left( {{1 \over 3} \times {2 \over 5}} \right) \times {3 \over 4} = {1 \over 3} \times \left( {{2 \over 5} \times {3 \over 4}} \right)$

+) $\displaystyle \displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} = {3 \over 5} \times {3 \over 4} = {{3 \times 3} \over {5 \times 4}} \displaystyle= {9 \over {20}}$ $\displaystyle \displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} = {3 \over 5} \times {3 \over 4} = {{3 \times 3} \over {5 \times 4}} \displaystyle= {9 \over {20}}$

$\displaystyle \displaystyle{1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4} = {{1 \times 3} \over {5 \times 4}} + {{2 \times 3} \over {5 \times 4}}$ $\displaystyle \displaystyle{1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4} = {{1 \times 3} \over {5 \times 4}} + {{2 \times 3} \over {5 \times 4}}$

$\displaystyle \displaystyle= {3 \over {20}} + {6 \over {20}} \displaystyle \displaystyle= {{3 + 6} \over {20}} = {9 \over {20}}$ $\displaystyle \displaystyle= {3 \over {20}} + {6 \over {20}} \displaystyle \displaystyle= {{3 + 6} \over {20}} = {9 \over {20}}$

Vậy: $\displaystyle \displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} = {1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4}$ $\displaystyle \displaystyle\left( {{1 \over 5} + {2 \over 5}} \right) \times {3 \over 4} = {1 \over 5} \times {3 \over 4} + {2 \over 5} \times {3 \over 4}$

b)

1) $\displaystyle \displaystyle{3 \over {22}} \times {3 \over {11}} \times 22;$ $\displaystyle \displaystyle{3 \over {22}} \times {3 \over {11}} \times 22;$

Cách 1:

$\displaystyle \displaystyle{3 \over {22}} \times {3 \over {11}} \times 22 = {{3 \times 3} \over {22 \times 11}} \times 22 \displaystyle \displaystyle= {9 \over {22 \times 11}} \times 22 = {{9 \times 22} \over {22 \times 11}} = {9 \over {11}}$ $\displaystyle \displaystyle{3 \over {22}} \times {3 \over {11}} \times 22 = {{3 \times 3} \over {22 \times 11}} \times 22 \displaystyle \displaystyle= {9 \over {22 \times 11}} \times 22 = {{9 \times 22} \over {22 \times 11}} = {9 \over {11}}$

Cách 2:

$\displaystyle \displaystyle{3 \over {22}} \times {3 \over {11}} \times 22 \displaystyle \displaystyle= {3 \over {22}} \times 22 \times {3 \over {11}} = {{3 \times 22} \over {22}} \times {3 \over {11}} \displaystyle \displaystyle= 3 \times {3 \over {11}} = {{3 \times 3} \over {11}} = {9 \over {11}}$ $\displaystyle \displaystyle{3 \over {22}} \times {3 \over {11}} \times 22 \displaystyle \displaystyle= {3 \over {22}} \times 22 \times {3 \over {11}} = {{3 \times 22} \over {22}} \times {3 \over {11}} \displaystyle \displaystyle= 3 \times {3 \over {11}} = {{3 \times 3} \over {11}} = {9 \over {11}}$

2) $\displaystyle \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5};$ $\displaystyle \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5};$

Cách 1:

$\displaystyle \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5} \displaystyle \displaystyle= \left( {{3 \over 6} + {2 \over 6}} \right) \times {2 \over 5} = {5 \over 6} \times {2 \over 5} \displaystyle \displaystyle= {{5 \times 2} \over {6 \times 5}} = {2 \over 6} = {1 \over 3}$ $\displaystyle \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5} \displaystyle \displaystyle= \left( {{3 \over 6} + {2 \over 6}} \right) \times {2 \over 5} = {5 \over 6} \times {2 \over 5} \displaystyle \displaystyle= {{5 \times 2} \over {6 \times 5}} = {2 \over 6} = {1 \over 3}$

Cách 2:

$\displaystyle \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5} = {1 \over 2} \times {2 \over 5} + {1 \over 3} \times {2 \over 5} \displaystyle = {{1 \times 2} \over {2 \times 5}} + {{1 \times 2} \over {3 \times 5}} \displaystyle \displaystyle= {1 \over 5} + {2 \over {15}} \displaystyle \displaystyle= {3 \over {15}} + {2 \over {15}} = {5 \over {15}} = {1 \over 3}$ $\displaystyle \displaystyle\left( {{1 \over 2} + {1 \over 3}} \right) \times {2 \over 5} = {1 \over 2} \times {2 \over 5} + {1 \over 3} \times {2 \over 5} \displaystyle = {{1 \times 2} \over {2 \times 5}} + {{1 \times 2} \over {3 \times 5}} \displaystyle \displaystyle= {1 \over 5} + {2 \over {15}} \displaystyle \displaystyle= {3 \over {15}} + {2 \over {15}} = {5 \over {15}} = {1 \over 3}$

3) $\displaystyle \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5}$ $\displaystyle \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5}$

Cách 1:

$\displaystyle \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5} \displaystyle = {{3 \times 17} \over {5 \times 21}} + {{17 \times 2} \over {21 \times 5}} \displaystyle \displaystyle= {{51} \over {105}} + {{34} \over {105}} \displaystyle \displaystyle= {{85} \over {105}} = {{85:5} \over {105:5}} = {{17} \over {21}}$ $\displaystyle \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5} \displaystyle = {{3 \times 17} \over {5 \times 21}} + {{17 \times 2} \over {21 \times 5}} \displaystyle \displaystyle= {{51} \over {105}} + {{34} \over {105}} \displaystyle \displaystyle= {{85} \over {105}} = {{85:5} \over {105:5}} = {{17} \over {21}}$

Cách 2:

$\displaystyle \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5} = {{17} \over {21}} \times \left( {{3 \over 5} + {2 \over 5}} \right) \displaystyle \displaystyle= {{17} \over {21}} \times {5 \over 5} \displaystyle \displaystyle= {{17} \over {21}} \times 1 = {{17} \over {21}}$ $\displaystyle \displaystyle{3 \over 5} \times {{17} \over {21}} + {{17} \over {21}} \times {2 \over 5} = {{17} \over {21}} \times \left( {{3 \over 5} + {2 \over 5}} \right) \displaystyle \displaystyle= {{17} \over {21}} \times {5 \over 5} \displaystyle \displaystyle= {{17} \over {21}} \times 1 = {{17} \over {21}}$

Giải Toán lớp 4 trang 134 Bài 2

Tính chu vi hình chữ nhật có chiều dài $\frac{4}{5}$ $\frac{4}{5}$ m và chiều rộng $\frac{2}{3}$ $\frac{2}{3}$ m.

Lời giải:

Chu vi hình chữ nhật là:

$\displaystyle \left( {{4 \over 5} + {2 \over 3}} \right) \times 2 = {{44} \over {15}}\;$ $\displaystyle \left( {{4 \over 5} + {2 \over 3}} \right) \times 2 = {{44} \over {15}}\;$(m)

Đáp số: $\displaystyle \displaystyle{{44} \over {15}}$ $\displaystyle \displaystyle{{44} \over {15}}$m.

Giải Toán lớp 4 trang 134 Bài 3

May một chiếc túi hết $\frac{2}{3}$ $\frac{2}{3}$ m vải. Hỏi may 3 chiếc túi hết mấy mét vải?

Lời giải:

May 3 chiếc túi hết số vải là:

$\frac{2}{3}$ $\frac{2}{3}$ x 3 = 2 (m)

Đáp số: 2m vải

Lý thuyết Phép nhân phân số

1. Phép nhân phân số Toán lớp 4

Quy tắc: Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

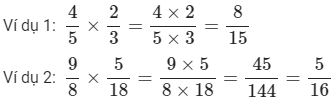
Lý thuyết Toán lớp 4: Phép nhân phân số

Lưu ý:

+) Sau khi làm phép nhân hai phân số, nếu thu được phân số chưa tối giản thì ta phải rút gọn thành phân số tối giản.

+) Khi nhân hai phân số, sau bước lấy tử số nhân tử số, mẫu số nhân mẫu số, nếu tử số và mẫu số cùng chia hết cho một số nào đó thì ta rút gọn luôn, không nên nhân lên sau đó lại rút gọn.

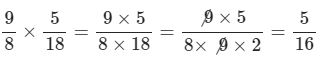
Lý thuyết Toán lớp 4: Phép nhân phân số

b) Các tính chất của phép nhân phân số

+) Tính chất giao hoán: Khi đổi chỗ các phân số trong một tích thì tích của chúng không thay đổi

a x b = b x a

+) Tính chất kết hợp: Khi nhân một tích hai phân số với phân số thứ ba, ta có thể nhân phân số thứ nhất với tích của hai phân số còn lại.

(a x b) x c = a x (b x c)

+ Tính chất phân phối: Khi nhân một tổng hai phân số với phân số thứ ba, ta có thể nhân lần lượt từng phân số của tổng với phân số thứ ba rồi cộng các kết quả đó lại với nhau.

(a + b) x c = a x c + b x c

+ Nhân với số 1: Phân số nào nhân với 1 cũng bằng chính phân số đó.

a x 1 = 1 x a = a

+ Nhân với số 0: Phân số nào nhân với 0 cũng bằng 0.

a x 0 = 0 x a = 0

2. Một số dạng bài tập phép nhân phân số

Dạng 1: Tìm tích của hai phân số

Phương pháp: Áp dụng quy tắc nhân hai phân số.

Dạng 2: Tính giá trị các biểu thức:

Phương pháp giải: Áp dụng các quy tắc tính giá trị biểu thức như ưu tiên tính trong ngoặc trước, thực hiện phép tính nhân, chia trước, phép cộng trừ sau …

Dạng 3: So sánh

Phương pháp: Tính giá trị các biểu thức, sau đó áp dụng các quy tắc so sánh phân số.

Dạng 4: Tìm x

Phương pháp giải: Xác định xem x đóng vai trò nào, từ đó tìm được x theo các quy tắc đã học lớp lớp 3.

Dạng 5: Tính nhanh

Phương pháp giải: Áp dụng các tính chất của phép nhân phân số nhóm các phân số có thể tính toán dễ dàng.

Dạng 6: Toán có lời văn

Video Luyện tập Toán 4 trang 134

Bài tập phép nhân phân số lớp 4

Trắc nghiệm Luyện tập phép nhân phân số

>> Xem toàn bộ: Trắc nghiệm Luyện tập phép nhân phân số

Ngoài ra, các em học sinh hoặc quý phụ huynh còn có thể tham khảo thêm Giải vở bài tập Toán 4: Luyện tập Phép nhân phân số hay đề thi học kì 1 lớp 4 và đề thi học kì 2 lớp 4 các môn Toán, Tiếng Việt, Tiếng Anh, Khoa, Sử, Địa, Tin học theo chuẩn kiến thức, kỹ năng của bộ Giáo Dục. Những đề thi này được VnDoc.com sưu tầm và chọn lọc từ các trường tiểu học trên cả nước nhằm mang lại cho học sinh lớp 4 những đề ôn thi học kì chất lượng nhất. Mời các em cùng quý phụ huynh tải miễn phí đề thi về và ôn luyện.

Chia sẻ, đánh giá bài viết

521

90.535

Bài trước

Bài sau

Chia sẻ bởi:
Nguyễn Minh Ngọc
Nhóm:
Sưu tầm
Ngày: 27/02/2023

Tải về

1 Bình luận

Sắp xếp theo

Xóa Đăng nhập để Gửi

Văn Hòa
Tại sao 22 nhân 11 lại bằng 22 câu này sai rồi nhé
Thích Phản hồi 0 11/03/23
- chang
  Đáp án đúng r ạ, bạn kiểm tra lại nhé
  Thích Phản hồi 0 11/03/23