Toán lớp 4 trang 122: So sánh hai phân số khác mẫu số

Lời Giải bài tập Toán lớp 4

So sánh hai phân số khác mẫu số

1. Lý thuyết So sánh hai phân số khác mẫu số
2. Toán lớp 4 trang 122 Bài 1
3. Toán lớp 4 trang 122 Bài 2
4. Toán lớp 4 trang 122 Bài 3
5. Bài tập So sánh hai phân số khác mẫu số

Giải bài tập trang 122 SGK Toán 4: So sánh hai phân số khác mẫu số với đáp án và hướng dẫn giải chi tiết. Lời giải hay bài tập toán 4 này sẽ giúp các em học sinh ôn tập, củng cố kiến thức nắm được cách so sánh hai phân khác mẫu số và áp dụng giải các bài tập liên quan. Sau đây, để học tốt Toán lớp 4, mời các em học sinh cùng tham khảo lời giải chi tiết cho bài tập sách giáo khoa môn Toán lớp 4 trang 122.

>> Bài trước: Toán lớp 4 trang 120: Luyện tập so sánh hai phân số có cùng mẫu số

Chúng ta đã biết cách so sánh hai phân số có cùng mẫu số bằng việc so sánh tử số của chúng. Vậy làm thế nào để biết cách so sánh hai phân số khác mẫu số, các bạn cùng tìm hiểu chi tiết Lý thuyết và cách giải các bài tập SGK sau đây:

1. Lý thuyết So sánh hai phân số khác mẫu số

Ví dụ: So sánh hai phân số $\dfrac{2}{3}$ $\dfrac{2}{3}$ và $\dfrac{3}{4}$ $\dfrac{3}{4}$.

a) Lấy hai băng giấy bằng nhau. Chia băng giấy thứ nhất thành 3 phần bằng nhau, lấy 2 phần, tức là lấy $\dfrac{2}{3}$ $\dfrac{2}{3}$ băng giấy. Chia băng giấy thứ hai thành 4 phần bằng nhau, lấy 3 phần, tức là lấy $\dfrac{3}{4}$ $\dfrac{3}{4}$ băng giấy.

Nhìn hình vẽ ta thấy:

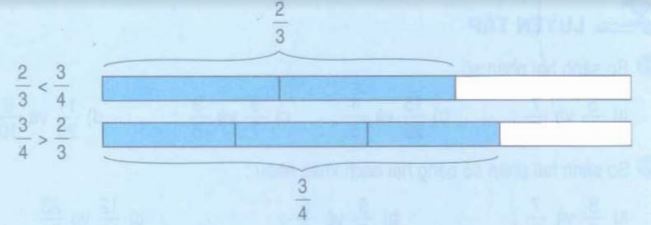
So sánh hai phân số khác mẫu số

b) Ta có thể so sánh hai phân số $\dfrac{2}{3}$ $\dfrac{2}{3}$ và $\dfrac{3}{4}$ $\dfrac{3}{4}$ như sau:

Quy đồng mẫu số hai phân số $\dfrac{2}{3}$ $\dfrac{2}{3}$ và $\dfrac{3}{4}$ $\dfrac{3}{4}$:

$\dfrac{2}{3}= \dfrac{2\times 4}{3\times 4}=\dfrac{8}{12}$ $\dfrac{2}{3}= \dfrac{2\times 4}{3\times 4}=\dfrac{8}{12}$;

$\dfrac{3}{4}= \dfrac{3 \times 3}{4 \times 3}=\dfrac{9}{12}$ $\dfrac{3}{4}= \dfrac{3 \times 3}{4 \times 3}=\dfrac{9}{12}$

So sánh hai phân số có cùng mẫu số :

$\dfrac{8}{12}< \dfrac{9}{12}$ $\dfrac{8}{12}< \dfrac{9}{12}$ (vì 8<9)

Kết luận: $\dfrac{2}{3}< \dfrac{3}{4}$ $\dfrac{2}{3}< \dfrac{3}{4}$.

Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.

>> Chi tiết: Lý thuyết So sánh hai phân số

Hướng dẫn giải bài SO SÁNH CÁC PHÂN SỐ KHÁC MẪU SỐ – SGK toán 4 (bài 1, 2, 3 SGK Toán lớp 4 trang 122). Các em học sinh cùng so sánh đối chiếu đáp án sau đây.

2. Toán lớp 4 trang 122 Bài 1

So sánh hai phân số:

a) $\displaystyle \displaystyle{3 \over 4} và \displaystyle \displaystyle{4 \over 5}$ $\displaystyle \displaystyle{3 \over 4} và \displaystyle \displaystyle{4 \over 5}$

b) $\displaystyle \displaystyle{5 \over 6} và \displaystyle \displaystyle{7 \over 8}$ $\displaystyle \displaystyle{5 \over 6} và \displaystyle \displaystyle{7 \over 8}$

c) $\displaystyle \displaystyle{2 \over 5} và \displaystyle \displaystyle{3 \over 10}.$ $\displaystyle \displaystyle{2 \over 5} và \displaystyle \displaystyle{3 \over 10}.$

Đáp án:

Hướng dẫn giải:

Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.

Đáp án

a) Quy đồng mẫu số hai phân số $\displaystyle{3 \over 4} và \displaystyle{4 \over 5}$ $\displaystyle{3 \over 4} và \displaystyle{4 \over 5}$:

$\displaystyle{3 \over 4} = {{3 \times 5} \over {4 \times 5}} = {{15} \over {20}};\quad {4 \over 5} = {{4 \times 4} \over {5 \times 4}} = {{16} \over {20}}$ $\displaystyle{3 \over 4} = {{3 \times 5} \over {4 \times 5}} = {{15} \over {20}};\quad {4 \over 5} = {{4 \times 4} \over {5 \times 4}} = {{16} \over {20}}$

Vì $\displaystyle{{15} \over {20}} < {{16} \over {20}} nên \displaystyle{3 \over 4}< \displaystyle{4 \over 5}$ $\displaystyle{{15} \over {20}} < {{16} \over {20}} nên \displaystyle{3 \over 4}< \displaystyle{4 \over 5}$.

b) Quy đồng mẫu số hai phân số $\displaystyle{5 \over 6} và \displaystyle{7 \over 8}$ $\displaystyle{5 \over 6} và \displaystyle{7 \over 8}$:

$\displaystyle{5 \over 6} = {{5 \times 8} \over {6 \times 8}} = {{40} \over {48}}; \quad {7 \over 8} = {{7 \times 6} \over {8 \times 6}} = {{42} \over {48}}$ $\displaystyle{5 \over 6} = {{5 \times 8} \over {6 \times 8}} = {{40} \over {48}}; \quad {7 \over 8} = {{7 \times 6} \over {8 \times 6}} = {{42} \over {48}}$

Vì $\displaystyle{{40} \over {48}} < {{42} \over {48}}$ $\displaystyle{{40} \over {48}} < {{42} \over {48}}$ nên $\displaystyle{5 \over 6} < \displaystyle{7 \over 8}$ $\displaystyle{5 \over 6} < \displaystyle{7 \over 8}$.

c) Quy đồng mẫu số phân số $\displaystyle{2 \over 5}$ $\displaystyle{2 \over 5}$ và giữ nguyên phân số $\displaystyle{3 \over 10}$ $\displaystyle{3 \over 10}$:

$\displaystyle{2 \over 5} = {{2 \times 2} \over {5 \times 2}} = {4 \over {10}}$ $\displaystyle{2 \over 5} = {{2 \times 2} \over {5 \times 2}} = {4 \over {10}}$

Vì $\displaystyle{4 \over {10}} > {3 \over {10}}$ $\displaystyle{4 \over {10}} > {3 \over {10}}$ nên $\displaystyle{2 \over 5} > \displaystyle{3 \over 10}$ $\displaystyle{2 \over 5} > \displaystyle{3 \over 10}$.

3. Toán lớp 4 trang 122 Bài 2

Rút gọn rồi so sánh hai phân số:

a) $\displaystyle \displaystyle{6 \over {10}} và \displaystyle \displaystyle{4 \over 5}$ $\displaystyle \displaystyle{6 \over {10}} và \displaystyle \displaystyle{4 \over 5}$

b) $\displaystyle \displaystyle{3 \over 4} và \displaystyle \displaystyle{6 \over {12}}$ $\displaystyle \displaystyle{3 \over 4} và \displaystyle \displaystyle{6 \over {12}}$

Hướng dẫn giải:

- Rút gọn các phân số đã cho thành phân số tối giản (nếu được).

- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.

Đáp án

a) Rút gọn phân số $\displaystyle{6 \over {10}}$ $\displaystyle{6 \over {10}}$ và giữ nguyên phân số $\displaystyle{4 \over 5}$ $\displaystyle{4 \over 5}$:

$\displaystyle{6 \over {10}} = {{6:2} \over {10:2}} = {3 \over 5}$ $\displaystyle{6 \over {10}} = {{6:2} \over {10:2}} = {3 \over 5}$

Vì $\displaystyle{3 \over 5}<{4 \over 5}$ $\displaystyle{3 \over 5}<{4 \over 5}$ nên $\displaystyle{6 \over {10}} < \displaystyle{4 \over 5}$ $\displaystyle{6 \over {10}} < \displaystyle{4 \over 5}$ .

b) Rút gọn phân số $\displaystyle{6 \over {12}}$ $\displaystyle{6 \over {12}}$ và giữ nguyên phân số $\displaystyle{6 \over {12}}$ $\displaystyle{6 \over {12}}$ :

$\displaystyle{6 \over {12}} = {{6:3} \over {12:3}} = {2 \over 4}$ $\displaystyle{6 \over {12}} = {{6:3} \over {12:3}} = {2 \over 4}$

Vì $\displaystyle{3 \over 4} > \displaystyle{2 \over 4}$ $\displaystyle{3 \over 4} > \displaystyle{2 \over 4}$nên $\displaystyle{3 \over 4} > \displaystyle{6 \over {12}}$ $\displaystyle{3 \over 4} > \displaystyle{6 \over {12}}$.

4. Toán lớp 4 trang 122 Bài 3

Mai ăn 3/8 cái bánh, Hoa ăn 2/5 cái bánh

Ai ăn nhiều bánh hơn?

Hướng dẫn giải:

Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.

Đáp án

Quy đồng mẫu số hai phân số:

$\displaystyle\eqalign{ & {3 \over 8} = {{3 \times 5} \over {8 \times 5}} = {{15} \over {40}} ; \cr & {2 \over 5} = {{2 \times 8} \over {5 \times 8}} = {{16} \over {40}} .\cr}$ $\displaystyle\eqalign{ & {3 \over 8} = {{3 \times 5} \over {8 \times 5}} = {{15} \over {40}} ; \cr & {2 \over 5} = {{2 \times 8} \over {5 \times 8}} = {{16} \over {40}} .\cr}$

Mai ăn $\frac{3}{8}$ $\frac{3}{8}$ tức là ăn $\frac{15}{40}$ $\frac{15}{40}$ cái bánh

Hoa ăn $\frac{2}{5}$ $\frac{2}{5}$ cái bánh tức là ăn $\frac{16}{40}$ $\frac{16}{40}$ cái bánh

Vì $\displaystyle{{16} \over {40}} > {{15} \over {40}}$ $\displaystyle{{16} \over {40}} > {{15} \over {40}}$ nên $\dfrac{2}{5} > \dfrac{3}{8}$ $\dfrac{2}{5} > \dfrac{3}{8}$.

Vậy Hoa là người ăn nhiều bánh hơn.

>> Bài tiếp theo: Giải bài tập trang 122 SGK Toán 4: Luyện tập so sánh hai phân số khác mẫu số

5. Bài tập So sánh hai phân số khác mẫu số

..........................

Ngoài ra, các em học sinh hoặc quý phụ huynh còn có thể tham khảo thêm đề thi học kì 1 lớp 4 và đề thi học kì 2 lớp 4 các môn Toán, Tiếng Việt, Tiếng Anh, Khoa, Sử, Địa, Tin học theo chuẩn thông tư 22 của bộ Giáo Dục. Những đề thi này được VnDoc.com sưu tầm và chọn lọc từ các trường tiểu học trên cả nước nhằm mang lại cho học sinh lớp 4 những đề ôn thi học kì chất lượng nhất. Mời các em cùng quý phụ huynh tải miễn phí đề thi về và ôn luyện.

Chia sẻ, đánh giá bài viết

849

175.132

Bài trước

Bài sau