Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Ôn thi vào lớp 10 chuyên đề 16: Bài toán cực trị hình học

Bài tập bất đẳng thức lớp 9

Bài trước

Tải về

Bài sau

Lớp: Lớp 9

Môn: Toán

Loại File: PDF

Phân loại: Tài liệu Tính phí

Chuyên đề Toán 9: Bất đẳng thức hình học

Ôn thi vào lớp 10 chuyên đề 16: Bài toán cực trị hình học được VnDoc.com sưu tầm nhằm giúp quá trình ôn tập và củng cố kiến thức chuẩn bị cho kì thi học kì mới môn Toán của các bạn học sinh lớp 9 trở nên thuận lợi hơn. Mời các bạn tham khảo

A. Cách giải bài toán cực trị hình học

1. Sử dụng mối quan hệ giữa đường xiên và đường vuông góc.

Từ điểm A ở ngoài đường thẳng d kẻ AH vuông góc với d. Với bất kì điểm B trên đường thẳng d ta có: AH ≤ AB. Dấu "= " xảy ra khi và chỉ khi B trùng với H.

2. Sử dụng quy tắc ba điểm

Với ba điểm bất kì A, B; C ta luôn có: AB ≤ AC + CB

Dấu "= " xảy ra khi và chỉ khi C là một điểm thuộc đoạn thẳng AB.

3. Sử dụng bất đẳng thức đại số: với x, y là các số không âm ta có:

$\frac{{{x^2} + {y^2}}}{2} \geqslant xy$ $\frac{{{x^2} + {y^2}}}{2} \geqslant xy$
$\frac{{x + y}}{2} \geqslant \sqrt {xy}$ $\frac{{x + y}}{2} \geqslant \sqrt {xy}$
$\frac{{{x^2} + {y^2}}}{2} \geqslant {\left( {\frac{{x + y}}{2}} \right)^2} \geqslant xy$ $\frac{{{x^2} + {y^2}}}{2} \geqslant {\left( {\frac{{x + y}}{2}} \right)^2} \geqslant xy$

Dấu "= " xảy ra khi và chỉ khi x = y.

B. Bài tập cực trị hình học

Bài 1. Tìm một hình chữ nhật nội tiếp đường tròn có diện tích lớn nhất.

Hướng dẫn giải

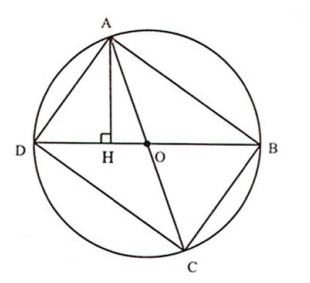
Giả sử hình chữ nhật ABCD nội tiếp đường tròn (O; R)

Cách 1: Kẻ AH vuông góc với DB.

Ta có:

$\begin{matrix} {S_{ABCD}} = 2{S_{ABD}} \hfill \\ \Rightarrow {S_{ABCD}} = 2.\frac{1}{2}BD.AH = 2R.AH \leqslant 2R.AO = 2{R^2} \hfill \\ \end{matrix}$ $\begin{matrix} {S_{ABCD}} = 2{S_{ABD}} \hfill \\ \Rightarrow {S_{ABCD}} = 2.\frac{1}{2}BD.AH = 2R.AH \leqslant 2R.AO = 2{R^2} \hfill \\ \end{matrix}$

Vậy diện tích hình chữ nhật ABCD lớn nhất bằng $2R^{2}$ $2R^{2}$ khi $H \equiv O$ $H \equiv O$ hay ABCD là hình vuông.

Cách 2. $\bigtriangleup ABC$ $\bigtriangleup ABC$ vuông tại B theo định lí Py-ta-go, ta có: ${AB}^{2} + {BC}^{2} = {AC}^{2} = 4R^{2}$ ${AB}^{2} + {BC}^{2} = {AC}^{2} = 4R^{2}$

Áp dụng bất đẳng thức Co -si, ta có:

$S_{ABCD} = AB \cdot BC \leq \frac{AB^{2} + BC^{2}}{2} = \frac{4R^{2}}{2} = 2R^{2}.$ $S_{ABCD} = AB \cdot BC \leq \frac{AB^{2} + BC^{2}}{2} = \frac{4R^{2}}{2} = 2R^{2}.$

Vậy diện tích hình chữ nhật ABCD lớn nhất bằng $2R^{2}$ $2R^{2}$ khi $AB = BC$ hay ABCD là hình vuông.

Nhận xét: Ý tưởng của hai lời giải trên là:

Nếu tam giác có một cạnh không đổi thì diện tích lớn nhất khi đường cao ứng với cạnh đó lớn nhất.

Các yếu tố về cạnh có tổng bình phương không đổi (tổng hai cạnh không đổi hoặc tích hai cạnh không đổi) thì ta có thể vận dụng bất đẳng thức đại số.

Bài 2. Trên đường tròn $(O;R)$ có dây $BC < 2R$ có định. Xác định vị trí điểm A trên cung lớn BC để:

a) Chu vi $\bigtriangleup ABC$ $\bigtriangleup ABC$ lớn nhất.

b) Diện tích $\bigtriangleup ABC$ $\bigtriangleup ABC$ lớn nhất.

Giải

Hình vẽ minh họa

a) Đặt $\widehat{BAC} = \alpha$ $\widehat{BAC} = \alpha$. Vì BC cố dịnh nên $\alpha$ $\alpha$ không dổi.

Trên tia đối của tia AB lấy $AM = AC$.

Suy ra $\bigtriangleup AMC$ $\bigtriangleup AMC$ cân tại A

$\Rightarrow \widehat{M_{1}} = \widehat{C_{1}} = \frac{1}{2}\widehat{BAC} = \frac{1}{2}\alpha$ $\Rightarrow \widehat{M_{1}} = \widehat{C_{1}} = \frac{1}{2}\widehat{BAC} = \frac{1}{2}\alpha$

$\Rightarrow M$ $\Rightarrow M$ thuộc cung chứa góc $\frac{1}{2}\alpha$ $\frac{1}{2}\alpha$ dựng trên đoạn thẳng BC (phần nửa mặt phằng bờ BC có chứa điểm A ).

Ta có chu vi $\bigtriangleup ABC$ $\bigtriangleup ABC$ là $AB + AC + BC = BM + BC$.

Chu vi $\bigtriangleup ABC$ $\bigtriangleup ABC$ lớn nhất $\Leftrightarrow BM$ $\Leftrightarrow BM$ lớn nhất $\Leftrightarrow BM$ $\Leftrightarrow BM$ là đường kính của đường

tròn chứa cung chứa góc $\frac{1}{2}\alpha \Leftrightarrow \widehat{BCM} = 90^{\circ} \Leftrightarrow AB = AC = AM$ $\frac{1}{2}\alpha \Leftrightarrow \widehat{BCM} = 90^{\circ} \Leftrightarrow AB = AC = AM$.

Hay A là diếm chính giữa cung lớn BC của dường tròn $(O;R)$.

b) (h.29) Cách 1. Kẻ $AH\bot BC,OM\bot BC$ $AH\bot BC,OM\bot BC$.

Ta có $S_{ABC} = \frac{1}{2}BC \cdot AH \leq \frac{1}{2}BC \cdot AM \leq \frac{1}{2}BC \cdot (AO + OM)$ $S_{ABC} = \frac{1}{2}BC \cdot AH \leq \frac{1}{2}BC \cdot AM \leq \frac{1}{2}BC \cdot (AO + OM)$.
Mà $BC,AO,OM$ không đổi nên diện tích $\bigtriangleup ABC$ $\bigtriangleup ABC$ lớn nhất bằng $\frac{1}{2}BC(AO + OM)$ $\frac{1}{2}BC(AO + OM)$.
Khi $H \equiv M;A,O,M$ $H \equiv M;A,O,M$ thẳng hàng $\Leftrightarrow A \equiv T$ $\Leftrightarrow A \equiv T$ là diểm chính giữa của cung lớn BC.

Cách 2. Kẻ tiếp tuyến xy // BC tiếp xúc với cung lớn BC tại T, khi đó T là diểm chính giữa của cung lớn BC.

Nếu A trùng với T thì AH là khoảng cách giữa xy và BC. Nếu A không trùng với T thì AH nhỏ hơn khoảng cách giữa xy và BC.

Mà $S_{ABC} = \frac{1}{2}BC \cdot AH$ $S_{ABC} = \frac{1}{2}BC \cdot AH$ nên $S_{ABC}$ $S_{ABC}$ lớn nhất $\Leftrightarrow AH$ $\Leftrightarrow AH$ lớn nhất $\Leftrightarrow A$ $\Leftrightarrow A$ trùng với $T$.

C. Bài tập tự rèn luyện

Bài 1:: Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Một đường thẳng d thay đổi đi qua A và cắt đường tròn (O); (O') lần lượt tại M và N (A nằm giữa M và N).

a. Chứng minh rằng góc MBN có giá trị không đổi.

b. Tìm vị trí của đường thẳng d để chu vi tam giác MBN lớn nhất.

c. Tìm vị trí của đường thẳng d để diện tích tam giác MBN lớn nhất.

Bài 2. Cho nửa đường tròn đường kính AB = 2R. Vẽ tiếp tuyến Ax. Lấy điểm M trên nửa đường tròn. Tia BM cắt Ax tại C. Xác định vị trí điểm M để 2BM + BC đạt giá trị nhỏ nhất.

Bài 3: Cho nửa đường tròn tâm O đường kính AB = 2R và điểm M thuộc nửa đường tròn, vẽ MH vuông góc với AB. Xác định vị trí điểm M để:

a. Diện tích tam giác OMH lớn nhất.

b. Chu vi tam giác OMH lớn nhất.

Bài 4. Cho đường tròn tâm O, đường kính AB = 2R và điểm C thuộc nửa đường tròn. Kẻ CH vuông góc với AB tại H. Gọi E và F lần lượt là hình chiếu của H trên AC và BC. Tìm vị trí của điểm C để:

a. Độ dài đoạn EF lớn nhất.

b. Tứ giác CEHF có diện tích lớn nhất.

Tài liệu dài, tải về để xem chi tiết và đầy đủ nhé!

.............................................

Ngoài Ôn thi vào lớp 10 chuyên đề 16: Bài toán cực trị hình học . Mời các bạn học sinh còn có thể tham khảo các đề thi học kì 2 lớp 9 các môn Toán, Văn, Anh, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề Thi vào lớp 10 năm 2019 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt

Tải về

Chọn file muốn tải về: