Các công thức vectơ trong không gian lớp 12
Công thức: Vectơ trong không gian
Trong chương trình Toán 12 , phần giải trí trong không gian là nền tảng quan sát giúp sinh học nắm vững kiến thức để giải quyết các bài toán về hình học không gian, góc độ Oxyz và các dạng bài liên quan đến góc – khoảng cách. Vì vậy, hệ thống hóa các công thức công thức trong không gian lớp 12 một cách đầy đủ, dễ hiểu và chính xác sẽ giúp bạn học nhanh, nhớ lâu và áp dụng hiệu quả trong luyện thi THPT Quốc gia. Bài viết dưới đây nằm trong Công thức toán 12 chuyên nghiệp , tổng hợp bộ công thức trọng tâm nhất kèm theo phân tích rõ ràng, hỗ trợ tối đa cho học sinh khi xem xét.
Công thức tính vectơ trong không gian Toán 12 đầy đủ được tổng hợp và đăng tải. Tài liệu này hệ thống các công thức vectơ một cách dễ hiểu, dễ nhớ giúp các bạn ôn tập kiến thức Toán 12 đầy đủ và nhanh nhất. Sau đây là tài liệu mời các bạn cùng tham khảo. Chúc các bạn học tập tốt!
A. Vectơ trong không gian
Định nghĩa: Vectơ trong không gian là một đoạn thẳng có hướng. Độ dài của vectơ trong không gian là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.
Chú ý: Tương tự như vectơ trong mặt phẳng, đối với vectơ trong không gian ta cũng có các kí hiệu và khái niệm sau:
- Vectơ có điểm đầu là
 \(A\) và điểm cuối là
\(A\) và điểm cuối là  \(B\) được kí hiệu là
\(B\) được kí hiệu là  \(\overrightarrow{AB}\).
\(\overrightarrow{AB}\). - Khi không cần chỉ rõ điểm đầu và điểm cuối của vectơ thì vectơ còn được kí hiệu là
 \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{x},\overrightarrow{y},\ldots\)
\(\overrightarrow{a},\overrightarrow{b},\overrightarrow{x},\overrightarrow{y},\ldots\) - Độ dài của vectơ
 \(\overrightarrow{AB}\) được kí hiệu là
\(\overrightarrow{AB}\) được kí hiệu là  \(\left| \overrightarrow{AB} \right|\), độ dài của vectơ
\(\left| \overrightarrow{AB} \right|\), độ dài của vectơ  \(\overrightarrow{a}\) được kí hiệu là
\(\overrightarrow{a}\) được kí hiệu là  \(\left| \overrightarrow{a}
\right|\)
\(\left| \overrightarrow{a}
\right|\) - Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó (Hình 1).
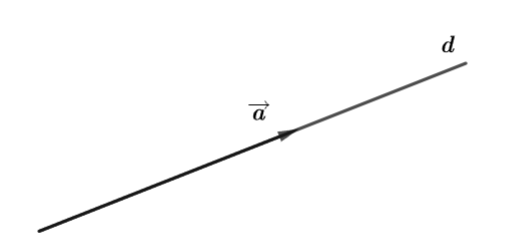
Hình 1. Đường thẳng ![]() \(d\) là giá của vectơ
\(d\) là giá của vectơ ![]() \(\overrightarrow{a}\)
\(\overrightarrow{a}\)
Tương tự như trường hợp của vectơ trong mặt phẳng, ta có các khái niệm sau đối với vectơ trong không gian:
- Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.
- Nếu hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.
- Hai vectơ
 \(\overrightarrow{a}\) và
\(\overrightarrow{a}\) và  \(\overrightarrow{b}\) được gọi là bằng nhau, kí hiệu
\(\overrightarrow{b}\) được gọi là bằng nhau, kí hiệu  \(\overrightarrow{a} =
\overrightarrow{b}\), nếu chúng có cùng độ dài và cùng hướng.
\(\overrightarrow{a} =
\overrightarrow{b}\), nếu chúng có cùng độ dài và cùng hướng.
Chú ý: Tương tự như vectơ trong mặt phẳng, ta có tính chất và các quy ước sau đối với vectơ trong không gian:Trong không gian, với mỗi điểm ![]() \(O\) và vectơ
\(O\) và vectơ ![]() \(\overrightarrow{a}\) cho trước, có duy nhất điểm
\(\overrightarrow{a}\) cho trước, có duy nhất điểm ![]() \(M\) sao cho
\(M\) sao cho ![]() \(\overrightarrow{OM} =
\overrightarrow{a}\)
\(\overrightarrow{OM} =
\overrightarrow{a}\)
- Các vectơ có điểm đầu và điểm cuối trùng nhau, ví dụ như
 \(\overrightarrow{AA},\overrightarrow{BB},\ldots\) gọi là các vectơ - không.
\(\overrightarrow{AA},\overrightarrow{BB},\ldots\) gọi là các vectơ - không. - Ta quy ước vectơ không có độ dài là 0, cùng hướng (và vì vậy cùng phương) với mọi vectơ.
- Do đó, các vectơ không đều bằng nhau và được kí hiệu chung là
 \(\overrightarrow{0}\).
\(\overrightarrow{0}\).
B. Tổng và hiệu của hai vectơ trong không gian
1) Tổng của hai vectơ trong không gian
Trong không gian, cho hai vectơ ![]() \(\overrightarrow{a}\) và
\(\overrightarrow{a}\) và ![]() \(\overrightarrow{b}\).
\(\overrightarrow{b}\).
Lấy một điểm ![]() \(A\) tùy ý, vẽ
\(A\) tùy ý, vẽ ![]() \(\overrightarrow{AB} = \overrightarrow{a}\),
\(\overrightarrow{AB} = \overrightarrow{a}\), ![]() \(\overrightarrow{BC} =
\overrightarrow{b}\).
\(\overrightarrow{BC} =
\overrightarrow{b}\).
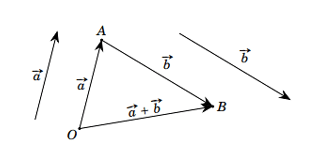
Vectơ ![]() \(\overrightarrow{AC}\) được gọi là tổng của hai vectơ
\(\overrightarrow{AC}\) được gọi là tổng của hai vectơ ![]() \(\overrightarrow{a}\) và
\(\overrightarrow{a}\) và ![]() \(\overrightarrow{b}\), kí hiệu
\(\overrightarrow{b}\), kí hiệu ![]() \(\overrightarrow{a} +
\overrightarrow{b}\).
\(\overrightarrow{a} +
\overrightarrow{b}\).
Vậy ![]() \(\overrightarrow{a} +
\overrightarrow{b} = \overrightarrow{AB} + \overrightarrow{BC} =
\overrightarrow{AC}\).
\(\overrightarrow{a} +
\overrightarrow{b} = \overrightarrow{AB} + \overrightarrow{BC} =
\overrightarrow{AC}\).
Phép lấy tổng hai vectơ còn được gọi là phép cộng vectơ.
Chú ý: Tương tự như phép cộng vectơ trong mặt phẳng, phép cộng vectơ trong không gian có các tình chất sau:
- Tính chất giao hoán:
 \(\overrightarrow{a}
+ \overrightarrow{b} = \overrightarrow{b} +
\overrightarrow{a}\).
\(\overrightarrow{a}
+ \overrightarrow{b} = \overrightarrow{b} +
\overrightarrow{a}\). - Tính chất kết hợp:
 \(\left(
\overrightarrow{a} + \overrightarrow{b} \right) + \overrightarrow{c} =
\overrightarrow{a} + \left( \overrightarrow{b} + \overrightarrow{c}
\right)\).
\(\left(
\overrightarrow{a} + \overrightarrow{b} \right) + \overrightarrow{c} =
\overrightarrow{a} + \left( \overrightarrow{b} + \overrightarrow{c}
\right)\). - Tính chất của vectơ-không:
 \(\overrightarrow{a} + \overrightarrow{0} =
\overrightarrow{0} + \overrightarrow{a} =
\overrightarrow{a}\).
\(\overrightarrow{a} + \overrightarrow{0} =
\overrightarrow{0} + \overrightarrow{a} =
\overrightarrow{a}\).
Đối với vectơ trong không gian, ta có các quy tắc sau:
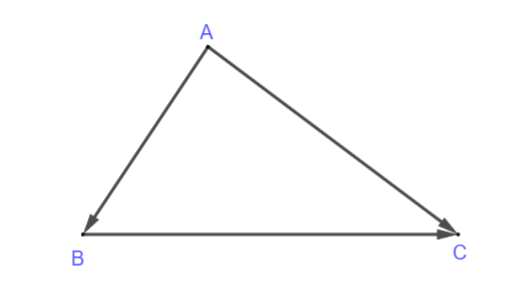
Quy tắc ba điểm
Với ba điểm ![]() \(A,B,C\) ta luôn có:
\(A,B,C\) ta luôn có: ![]() \(\overrightarrow{AB} + \overrightarrow{BC} =
\overrightarrow{AC}\)
\(\overrightarrow{AB} + \overrightarrow{BC} =
\overrightarrow{AC}\)
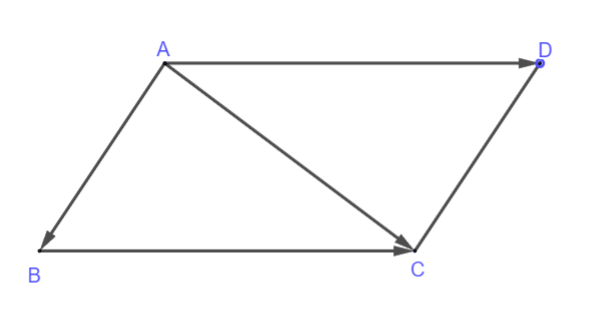
Quy tắc hình bình hành
Nếu ![]() \(ABCD\) là hình bình hành, ta có:
\(ABCD\) là hình bình hành, ta có: ![]() \(\overrightarrow{AB} +
\overrightarrow{AD} = \overrightarrow{AC}\).
\(\overrightarrow{AB} +
\overrightarrow{AD} = \overrightarrow{AC}\).
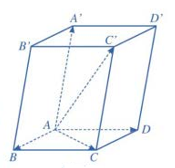
Quy tắc hình hộp
Cho hình hộp  \(ABCD.A'B'C'D'\), ta có:
\(ABCD.A'B'C'D'\), ta có:  \(\overrightarrow{AB} + \overrightarrow{AD} +
\overrightarrow{AA'} = \overrightarrow{AC'}\)
\(\overrightarrow{AB} + \overrightarrow{AD} +
\overrightarrow{AA'} = \overrightarrow{AC'}\)
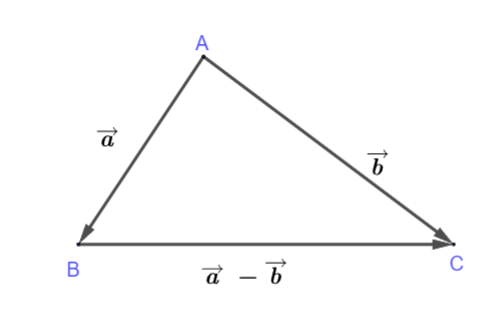
b. Hiệu của hai vectơ
Trong không gian, cho hai vectơ ![]() \(\overrightarrow{a}\) và
\(\overrightarrow{a}\) và ![]() \(\overrightarrow{b}\). Hiệu của vectơ
\(\overrightarrow{b}\). Hiệu của vectơ ![]() \(\overrightarrow{a}\) và vectơ
\(\overrightarrow{a}\) và vectơ ![]() \(\overrightarrow{b}\) là tổng vectơ
\(\overrightarrow{b}\) là tổng vectơ ![]() \(\overrightarrow{a}\) và vectơ đối của vectơ
\(\overrightarrow{a}\) và vectơ đối của vectơ ![]() \(\overrightarrow{b}\) , kí hiệu
\(\overrightarrow{b}\) , kí hiệu ![]() \(\overrightarrow{a} -
\overrightarrow{b}\).
\(\overrightarrow{a} -
\overrightarrow{b}\).
Phép lấy hiệu hai vectơ còn được gọi là phép trừ vectơ.
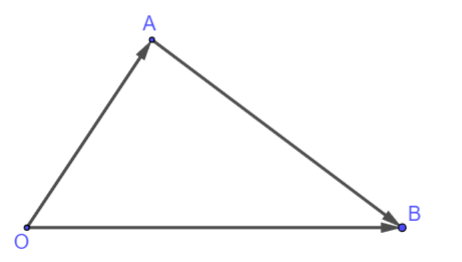
Chú ý: Trong không gian, với ba điểm ![]() \(O,A,B\) tùy ý, ta luôn có:
\(O,A,B\) tùy ý, ta luôn có: ![]() \(\overrightarrow{OB} - \overrightarrow{OA} =
\overrightarrow{AB}\).
\(\overrightarrow{OB} - \overrightarrow{OA} =
\overrightarrow{AB}\).
c. Tích của một số với một vectơ trong không gian
a. Định nghĩa:
Cho số ![]() \(k \neq 0\) và một vectơ
\(k \neq 0\) và một vectơ ![]() \(\overrightarrow{a} \neq
\overrightarrow{0}\). Tích của vectơ
\(\overrightarrow{a} \neq
\overrightarrow{0}\). Tích của vectơ ![]() \(\overrightarrow{a}\) với số
\(\overrightarrow{a}\) với số ![]() \(k\) là một vectơ, kí hiệu
\(k\) là một vectơ, kí hiệu ![]() \(k\overrightarrow{a}\).
\(k\overrightarrow{a}\).
Vectơ ![]() \(k\overrightarrow{a}\)cùng hướng với
\(k\overrightarrow{a}\)cùng hướng với ![]() \(\overrightarrow{a}\) nếu
\(\overrightarrow{a}\) nếu ![]() \(k > 0\), ngược hướng với
\(k > 0\), ngược hướng với ![]() \(\overrightarrow{a}\) nếu
\(\overrightarrow{a}\) nếu ![]() \(k < 0\) và có độ dài bằng
\(k < 0\) và có độ dài bằng ![]() \(|k|\left| \overrightarrow{a} \right|\).
\(|k|\left| \overrightarrow{a} \right|\).
Phép lấy tích của một số với một vectơ gọi là phép nhân một số với một vectơ.
Quy ước: ![]() \(0.\overrightarrow{a} =
\overrightarrow{0}\) và
\(0.\overrightarrow{a} =
\overrightarrow{0}\) và ![]() \(k.\overrightarrow{a} =
\overrightarrow{0}\).
\(k.\overrightarrow{a} =
\overrightarrow{0}\).
b. Tính chất:
Với hai vectơ ![]() \(\overrightarrow{a}\),
\(\overrightarrow{a}\), ![]() \(\overrightarrow{b}\)bất kỳ, với mọi số thực
\(\overrightarrow{b}\)bất kỳ, với mọi số thực ![]() \(h\) và
\(h\) và ![]() \(k\), ta có:
\(k\), ta có:
 \(k\left( \overrightarrow{a} +
\overrightarrow{b} \right) = k\overrightarrow{a} +
k\overrightarrow{b};k\left( \overrightarrow{a} - \overrightarrow{b}
\right) = k\overrightarrow{a} - k\overrightarrow{b}\)
\(k\left( \overrightarrow{a} +
\overrightarrow{b} \right) = k\overrightarrow{a} +
k\overrightarrow{b};k\left( \overrightarrow{a} - \overrightarrow{b}
\right) = k\overrightarrow{a} - k\overrightarrow{b}\) \((h + k)\overrightarrow{a} =
h\overrightarrow{a} + k\overrightarrow{a}\)
\((h + k)\overrightarrow{a} =
h\overrightarrow{a} + k\overrightarrow{a}\) \(h\left( k\overrightarrow{a} \right) =
(hk)\overrightarrow{a}\)
\(h\left( k\overrightarrow{a} \right) =
(hk)\overrightarrow{a}\) \(1\overrightarrow{a} =
\overrightarrow{a}\),
\(1\overrightarrow{a} =
\overrightarrow{a}\),  \(( -
1)\overrightarrow{a} = - \overrightarrow{a}\).
\(( -
1)\overrightarrow{a} = - \overrightarrow{a}\).
Chú ý:
- Hai vectơ
 \(\overrightarrow{a}\) và
\(\overrightarrow{a}\) và  \(\overrightarrow{b}\)(
\(\overrightarrow{b}\)( \(\overrightarrow{b}\) khác
\(\overrightarrow{b}\) khác  \(\overrightarrow{0}\)) cùng phương khi và chỉ khi có số
\(\overrightarrow{0}\)) cùng phương khi và chỉ khi có số  \(k\) sao cho
\(k\) sao cho  \(\overrightarrow{a} =
k\overrightarrow{b}\).
\(\overrightarrow{a} =
k\overrightarrow{b}\). - Ba điểm phân biệt
 \(A,B,C\) thẳng hàng khi và chỉ khi có số
\(A,B,C\) thẳng hàng khi và chỉ khi có số  \(k\) khác 0 sao cho
\(k\) khác 0 sao cho  \(\overrightarrow{AB} =
k\overrightarrow{AC}\).
\(\overrightarrow{AB} =
k\overrightarrow{AC}\). - Hệ thức trung điểm đoạn thẳng: Nếu
 \(I\) là trung điểm của đoạn thẳng
\(I\) là trung điểm của đoạn thẳng  \(AB\),
\(AB\),  \(M\) tuỳ ý, ta có:
\(M\) tuỳ ý, ta có:
![]() \(\overrightarrow{IA} + \overrightarrow{IB}
= \overrightarrow{0};\ \ \overrightarrow{MA} + \overrightarrow{MB} =
2\overrightarrow{MI}\).
\(\overrightarrow{IA} + \overrightarrow{IB}
= \overrightarrow{0};\ \ \overrightarrow{MA} + \overrightarrow{MB} =
2\overrightarrow{MI}\).
- Hệ thức trọng tâm tam giác: Nếu
 \(G\) là trọng tâm của tam giác
\(G\) là trọng tâm của tam giác  \(ABC\),
\(ABC\),  \(M\) tuỳ ý, ta có:
\(M\) tuỳ ý, ta có:
![]() \(\overrightarrow{GA} +
\overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0};\ \
\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} =
3\overrightarrow{MG}\)
\(\overrightarrow{GA} +
\overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0};\ \
\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} =
3\overrightarrow{MG}\)
- Hệ thức trọng tâm tứ diện: Cho
 \(G\) là trọng tâm của tứ diện
\(G\) là trọng tâm của tứ diện  \(ABCD\),
\(ABCD\),  \(M\) tuỳ ý. Ta có:
\(M\) tuỳ ý. Ta có:
![]() \(\overrightarrow{GA} +
\overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} =
\overrightarrow{0};\overrightarrow{MA} + \overrightarrow{MB} +
\overrightarrow{MC} + \overrightarrow{MD} =
4\overrightarrow{MG}\)
\(\overrightarrow{GA} +
\overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} =
\overrightarrow{0};\overrightarrow{MA} + \overrightarrow{MB} +
\overrightarrow{MC} + \overrightarrow{MD} =
4\overrightarrow{MG}\)
D. Tích vô hướng của hai vectơ trong không gian
a. Góc giữa hai vectơ
Trong không gian, cho hai vectơ ![]() \(\overrightarrow{a}\) và
\(\overrightarrow{a}\) và ![]() \(\overrightarrow{b}\) đều khác vectơ
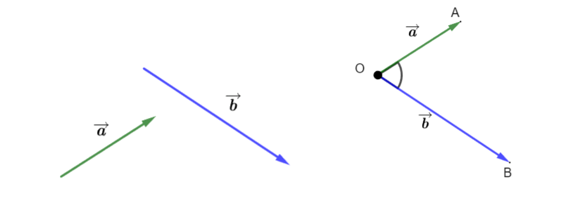
\(\overrightarrow{b}\) đều khác vectơ ![]() \(\overrightarrow{0}.\) Từ một điểm
\(\overrightarrow{0}.\) Từ một điểm ![]() \(O\) bất kì ta vẽ
\(O\) bất kì ta vẽ ![]() \(\overrightarrow{OA} = \overrightarrow{a}\) và
\(\overrightarrow{OA} = \overrightarrow{a}\) và ![]() \(\overrightarrow{OB} =
\overrightarrow{b}\). Góc cho hai vectơ
\(\overrightarrow{OB} =
\overrightarrow{b}\). Góc cho hai vectơ ![]() \(\overrightarrow{a}\) và
\(\overrightarrow{a}\) và ![]() \(\overrightarrow{b}\) trong không gian, kí hiệu
\(\overrightarrow{b}\) trong không gian, kí hiệu ![]() \(\left(
\overrightarrow{a},\overrightarrow{b} \right)\), là góc giữa hai vectơ
\(\left(
\overrightarrow{a},\overrightarrow{b} \right)\), là góc giữa hai vectơ ![]() \(\overrightarrow{OA},\overrightarrow{OB}\).
\(\overrightarrow{OA},\overrightarrow{OB}\).
Chú ý:
• ![]() \(0^{o} \leq \left(
\overrightarrow{a},\overrightarrow{b} \right) \leq 180^{o}\)
\(0^{o} \leq \left(
\overrightarrow{a},\overrightarrow{b} \right) \leq 180^{o}\)
• Nếu ![]() \(\left(
\overrightarrow{a},\overrightarrow{b} \right) = 90^{0}\) thì ta nói rằng
\(\left(
\overrightarrow{a},\overrightarrow{b} \right) = 90^{0}\) thì ta nói rằng ![]() \(\overrightarrow{a}\) và
\(\overrightarrow{a}\) và ![]() \(\overrightarrow{b}\)vuông góc với nhau, kí hiệu là
\(\overrightarrow{b}\)vuông góc với nhau, kí hiệu là ![]() \(\overrightarrow{a}\bot\overrightarrow{b}\).
\(\overrightarrow{a}\bot\overrightarrow{b}\).
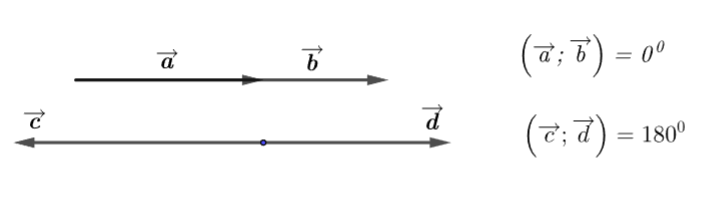
• Góc giữa hai vectơ cùng hướng và khác ![]() \(\overrightarrow{0}\) luôn bằng
\(\overrightarrow{0}\) luôn bằng ![]() \(0^{o}\).
\(0^{o}\).
• Góc giữa hai vectơ ngược hướng và khác ![]() \(\overrightarrow{0}\) luôn bằng
\(\overrightarrow{0}\) luôn bằng ![]() \(180^{o}\).
\(180^{o}\).
b. Tích vô hướng của hai vectơ
Trong không gian, cho hai vectơ ![]() \(\overrightarrow{a}\) và
\(\overrightarrow{a}\) và ![]() \(\overrightarrow{b}\) đều khác vectơ
\(\overrightarrow{b}\) đều khác vectơ ![]() \(\overrightarrow{0}.\) Tích vô hướng của hai vectơ
\(\overrightarrow{0}.\) Tích vô hướng của hai vectơ ![]() \(\overrightarrow{a}\) và
\(\overrightarrow{a}\) và ![]() \(\overrightarrow{b}\) là một số thực, kí hiệu
\(\overrightarrow{b}\) là một số thực, kí hiệu ![]() \(\overrightarrow{a}.\overrightarrow{b}\), được xác định bởi công thức sau:
\(\overrightarrow{a}.\overrightarrow{b}\), được xác định bởi công thức sau: ![]() \(\overrightarrow{a}.\overrightarrow{b} = \left|
\overrightarrow{a} \right|.\left| \overrightarrow{b} \right|\cos\left(
\overrightarrow{a},\overrightarrow{b} \right)\)
\(\overrightarrow{a}.\overrightarrow{b} = \left|
\overrightarrow{a} \right|.\left| \overrightarrow{b} \right|\cos\left(
\overrightarrow{a},\overrightarrow{b} \right)\)
Chú ý:
• Trường hợp có ít nhất một trong hai vectơ ![]() \(\overrightarrow{a}\) và
\(\overrightarrow{a}\) và ![]() \(\overrightarrow{b}\) bằng
\(\overrightarrow{b}\) bằng ![]() \(\overrightarrow{0}\), ta quy ước
\(\overrightarrow{0}\), ta quy ước ![]() \(\overrightarrow{a}.\overrightarrow{b} =
0\).
\(\overrightarrow{a}.\overrightarrow{b} =
0\).
• Với hai vectơ ![]() \(\overrightarrow{a}\) và
\(\overrightarrow{a}\) và ![]() \(\overrightarrow{b}\) đều khác vectơ
\(\overrightarrow{b}\) đều khác vectơ ![]() \(\overrightarrow{0}\), ta có
\(\overrightarrow{0}\), ta có ![]() \(\overrightarrow{a}\bot\overrightarrow{b}
\Leftrightarrow \overrightarrow{a}.\overrightarrow{b} = 0\).
\(\overrightarrow{a}\bot\overrightarrow{b}
\Leftrightarrow \overrightarrow{a}.\overrightarrow{b} = 0\).
• Khi ![]() \(\overrightarrow{a} =
\overrightarrow{b}\) thì tích vô hướng
\(\overrightarrow{a} =
\overrightarrow{b}\) thì tích vô hướng ![]() \(\overrightarrow{a}.\overrightarrow{b}\) được kí hiệu là
\(\overrightarrow{a}.\overrightarrow{b}\) được kí hiệu là ![]() \({\overrightarrow{a}}^{2}\) và được gọi là bình phương vô hướng của vectơ
\({\overrightarrow{a}}^{2}\) và được gọi là bình phương vô hướng của vectơ ![]() \(\overrightarrow{a}\).
\(\overrightarrow{a}\).
Ta có ![]() \({\overrightarrow{a}}^{2} = \left|
\overrightarrow{a} \right|.\left| \overrightarrow{a} \right|\cos 0^{o} =
\left| \overrightarrow{a} \right|^{2}\). Vậy bình phương vô hướng của một vectơ luôn bằng bình phương độ dài của vectơ đó.
\({\overrightarrow{a}}^{2} = \left|
\overrightarrow{a} \right|.\left| \overrightarrow{a} \right|\cos 0^{o} =
\left| \overrightarrow{a} \right|^{2}\). Vậy bình phương vô hướng của một vectơ luôn bằng bình phương độ dài của vectơ đó.
• Tính chất của tích vô hướng: Với ba vectơ ![]() \(\overrightarrow{a},\ \overrightarrow{b},\
\overrightarrow{c}\) bất kì và mọi số
\(\overrightarrow{a},\ \overrightarrow{b},\
\overrightarrow{c}\) bất kì và mọi số ![]() \(k\), ta có:
\(k\), ta có:
 \(\overrightarrow{a}.\overrightarrow{b} =
\overrightarrow{b}.\overrightarrow{a}\) (tính chất giao hoán)
\(\overrightarrow{a}.\overrightarrow{b} =
\overrightarrow{b}.\overrightarrow{a}\) (tính chất giao hoán) \(\overrightarrow{a}\left(
\overrightarrow{b} + \overrightarrow{c} \right) =
\overrightarrow{a}.\overrightarrow{b} +
\overrightarrow{a}.\overrightarrow{c}\) (tính chất phân phối)
\(\overrightarrow{a}\left(
\overrightarrow{b} + \overrightarrow{c} \right) =
\overrightarrow{a}.\overrightarrow{b} +
\overrightarrow{a}.\overrightarrow{c}\) (tính chất phân phối) \(\left( k\overrightarrow{a}
\right).\overrightarrow{b} = k\left(
\overrightarrow{a}.\overrightarrow{b} \right) =
\overrightarrow{a}.\left( k\overrightarrow{b} \right)\)
\(\left( k\overrightarrow{a}
\right).\overrightarrow{b} = k\left(
\overrightarrow{a}.\overrightarrow{b} \right) =
\overrightarrow{a}.\left( k\overrightarrow{b} \right)\)
Nhận xét: Từ các tính chất của tích vô hướng của hai vectơ ta suy ra:
 \(\left( \overrightarrow{a} + \overrightarrow{b}
\right)^{2} = {\overrightarrow{a}}^{2} +
2\overrightarrow{a}.\overrightarrow{b} +
{\overrightarrow{b}}^{2}\)
\(\left( \overrightarrow{a} + \overrightarrow{b}
\right)^{2} = {\overrightarrow{a}}^{2} +
2\overrightarrow{a}.\overrightarrow{b} +
{\overrightarrow{b}}^{2}\)  \(\left( \overrightarrow{a} - \overrightarrow{b}
\right)^{2} = {\overrightarrow{a}}^{2} -
2\overrightarrow{a}.\overrightarrow{b} +
{\overrightarrow{b}}^{2}\)
\(\left( \overrightarrow{a} - \overrightarrow{b}
\right)^{2} = {\overrightarrow{a}}^{2} -
2\overrightarrow{a}.\overrightarrow{b} +
{\overrightarrow{b}}^{2}\) \(\left( \overrightarrow{a} + \overrightarrow{b}
\right)\left( \overrightarrow{a} - \overrightarrow{b} \right) =
{\overrightarrow{a}}^{2} - {\overrightarrow{b}}^{2}\)
\(\left( \overrightarrow{a} + \overrightarrow{b}
\right)\left( \overrightarrow{a} - \overrightarrow{b} \right) =
{\overrightarrow{a}}^{2} - {\overrightarrow{b}}^{2}\)
---------------------------------------------------
Với hệ thống công thức thực hiện trong lớp 12 được trình bày rõ ràng, khoa học và ghi nhớ dễ dàng, bạn hoàn toàn có thể tự động áp dụng vào việc giải các dạng bài học không gian Oxyz từ cơ bản nâng cao. Tài liệu này không chỉ giúp bạn nắm chắc kiến thức tâm trí mà còn hỗ trợ tối ưu trong quá trình luyện thi THPT Quốc gia.
Đừng quên lưu lại bài viết để xem thường xuyên và khám phá thêm nhiều chuyên môn thuộc mục Công thức toán 12 như công thức khoảng cách, góc giữa đường thẳng, phương trình mặt thẳng, phương trình đường thẳng,… Mỗi nội dung đều được biên soạn theo sát chương trình học, giúp bạn tăng tốc độ làm bài và cải thiện điểm số một hiệu quả.
Nếu bạn muốn tổng hợp các bài tập vận dụng, hãy gửi tệp PDF công thức hoặc mở rộng các chương trình còn lại của Toán 12, hãy để lại yêu cầu — mình luôn sẵn sàng hỗ trợ bạn tốt nhất!










