Cho tam giác ABC cân tại A, kẻ BH vuông góc với AC (H thuộc AC), kẻ CK vuông góc với AB (K thuộc BC). Chứng minh AH = AK

Giải Toán 7 Hình học chương 2

2 3.913

"Cho tam giác ABC cân tại A, kẻ BH vuông góc với AC (H thuộc AC), kẻ CK vuông góc với AB (K thuộc BC). Chứng minh AH = AK" là một dạng bài tập điển hình của dạng bài tam giác cân trong chương trình Toán lớp 7. Tài liệu này được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 7, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 7 sau: Nhóm Tài liệu học tập lớp 7. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

I. Kiến thức cần nhớ về tam giác cân

1. Định nghĩa

+ Tam giác cân là tam giác có hai cạnh bên bằng nhau. Đỉnh của tam giác cân là giao điểm của hai cạnh bên. Góc được tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn lại là góc đáy

Bài tập Toán lớp 7: Tam giác cân

+ Tam giác ABC cân tại A $\Rightarrow \left\{ \begin{array}{l} AB = AC\\ \widehat B = \widehat C \end{array} \right.$

2. Tính chất

+ Tính chất 1: Trong tam giác cân hai ở đáy bằng nhau

+ Tính chất 2: Tam giác có hai góc bằng nhau là tam giác cân

II. Bài tập ví dụ về tam giác cân

Bài 1: Cho tam giác ABC cân tại A, kẻ BH vuông góc với AC (H thuộc AC), kẻ CK vuông góc với AB (K thuộc BC). Chứng minh AH = AK.

Lời giải:

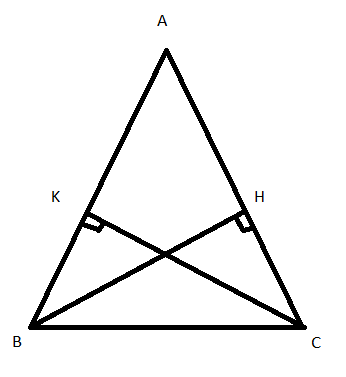
Bài tập Toán lớp 7: Tam giác cân

+ Có tam giác ABC là tam giác cân tại A $\left\{ \begin{array}{l} AB = AC\\ \widehat {ABC} = \widehat {ACB} \end{array} \right.$ (tính chất)

+ Có BH vuông góc với AC $\Rightarrow \widehat {BHC} = {90^0} \Rightarrow \widehat {HBC} + \widehat {BCH} = {90^0}$

Có CK vuông góc với AB $\Rightarrow \widehat {BKC} = {90^0} \Rightarrow \widehat {KBC} + \widehat {BCK} = {90^0}$

Mà $\widehat {ABC} = \widehat {ACB}$

Suy ra $\widehat {HBC} = \widehat {KCB}$ (cùng phụ với hai góc bằng nhau)

+ Xét tam giác BKC và tam giác CHB có:

$\widehat {BHC} = \widehat {BKC}\left( { = {{90}^0}} \right)$

BC chung

$\widehat {HBC} = \widehat {KCB}$ (cmt)

Suy ra $\Delta BKC = \Delta CHB$ (g.c.c)

Suy ra BK = HC (cặp cạnh tương ứng)

+ Có AK + KB = AB và AH + HC = AC

Mà AB = AC (cmt) và BK = HC (cmt)

Suy ra AK = AH (đpcm)

Bài 2 Cho tam giác ABC, đường phân giác AD (D thuộc BC), kẻ tia Dx song song với AB, tia Dx cắt AC tại E. Chứng minh tam giác ADE là tam giác cân.

Lời giải:

Bài tập Toán lớp 7: Tam giác cân

+ Có AD là phân giác của góc $\widehat {BAC} \Rightarrow \widehat {BAD} = \widehat {DAC}$ (tính chất)

Lại có DE // AB (Dx // AB – E thuộc Dx) $\Rightarrow \widehat {ABD} = \widehat {ADE}$ (so le trong)

Suy ra $\widehat {DAE} = \widehat {ADE}$

+ Xét tam giác ADE có: $\widehat {DAE} = \widehat {ADE}$

Suy ra tam giác ADE cân tại E (tính chất)

III. Bài tập vận dụng về tam giác cân

Bài 1: Cho tam giác cân DEF (DE = DF). Trên cạnh EF lấy hai điểm I, K sao cho EI = FK. Chứng minh DI = DK

Bài 2: Cho tam giác ABC cân tại A (AB = AC), trung tuyến AM. Gọi D là điểm nằm giữa A và M. Chứng minh rằng:

a, AM là tia phân giác của góc A

b, Tam giác ABD bằng tam giác ACD

c, Tam giác BCD là tam giác cân

Bài 3: Cho tam giác cân ABC có AB = AC. Trên cạnh Ab và AC lấy tương ứng hai điểm D và E sao cho AD = AE. Gọi M là trung điểm của BC. Chứng minh:

a, BE = CD

b, Tam giác AMD bằng tam giác AME

c, DE // BC

Bài 4: Cho tam giác ABC, AB = A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh:

a, Tam giác ADE cân

b, Tam giác ABD bằng tam giác ACE

Bài 5: Cho tam giác ABC cân tại A. Lấy điểm H thuộc cạnh AC, lấy điểm K thuộc cạnh AB sao cho AH = AK. Gọi O là giao điểm của BH và CK. Chứng minh rằng tam giác OBC là tam giác cân

---------------

Trên đây VnDoc đã giới thiệu tới các bạn Bài tập Toán 7: Tam giác cân. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 7, Giải bài tập Toán lớp 7, Giải VBT Toán lớp 7 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc

Đánh giá bài viết

2 3.913

Bài trước

Bài sau