Chứng minh rằng biểu thức không đổi khi điểm M di chuyển trên đường tròn
Dạng toán điểm M di chuyển trên đường tròn
Trong chương trình Hình học 9, dạng bài toán chứng minh biểu thức không đổi khi điểm M di chuyển trên đường tròn là một chuyên đề quan trọng, thường xuất hiện trong các đề kiểm tra và đề thi vào 10. Bài viết này sẽ giúp bạn hiểu rõ bản chất của bài toán quỹ tích, nắm vững cách chứng minh biểu thức không đổi, đồng thời cung cấp các ví dụ minh họa chi tiết, phương pháp giải và đáp án chuẩn. Qua đó, học sinh có thể vận dụng linh hoạt kiến thức hình học và đại số để xử lý hiệu quả các dạng bài tương tự trong đề thi.
Bài tập 1. Cho góc 
\(\widehat{xOy} =
60^{o}\). Đường tròn tâm K bán kính R tiếp xúc với Ox tại A và Oy tại B. Từ điểm M trên cung nhỏ AB, vẽ tiếp tuyến với đường tròn, tiếp tuyến này cắt Ox, Oy lần lượt tại C và D.
a) Tính chu vi \(\Delta COD\) theo R. Chứng tỏ chu vi đó không đổi khi M chạy trên cung nhỏ AB.
b) Chứng tỏ số đo \(\widehat{CKD}\) không đổi khi M chạy trên cung nhỏ AB.
Hướng dẫn giải
Hình vẽ minh họa:
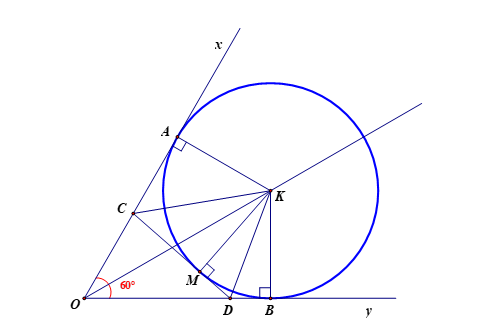
a) Ta có OA, OB là hai tiếp tuyến của (O) nên OA = OB và OK là phân giác của \(\widehat{AOB}\)
\(\Rightarrow \widehat{AOK} =
\widehat{BOK} = \frac{\widehat{AOB}}{2} = \frac{60^{o}}{2} =
30^{o}\)
Do đó \(\Delta OAK\) là nửa tam giác đều có cạnh AK = R \(\Rightarrow\)OK = 2R nên
OA = OB \(= \sqrt{OK^{2} - AK^{2}} =
\sqrt{(2R)^{2} - R^{2}} = R\sqrt{3}\)
Lại có CD tiếp xúc với (K) tại M nên CM = CA và DM = DB
Gọi p là chu vi của \(\Delta OCD\), ta có
\(p_{OCD}\)= OC + CM + MD + OD
= OC + CA + DB + OD
= 2 OA = 2\(R\sqrt{3}\)(không đổi)
b) Ta có CK là phân giác của \(\widehat{AKM}\)
DK là phân giác của \(\widehat{BKM}\)
Mà \(\widehat{AKM} + \widehat{BKM} =
\widehat{AKB} = 120^{o}\) (vì \(\widehat{O} = 60^{o}\) và \(\widehat{A} = \widehat{B} = 90^{o}\))
\(\Rightarrow \widehat{CKD} =
\frac{1}{2}\widehat{AKB} = \frac{1}{2}.120^{o} = 60^{o}\) (không đổi)
Bài tập 2. Từ một điểm A ở bên ngoài đường tròn (O), kẻ hai tiếp tuyến AB và AC với đường tròn. Từ một điểm M trên cung tròn trên cung nhỏ BC kẻ một tiếp tuyến thứ ba cắt hai tiếp tuyến kia tại P và Q. Chứng minh rằng khi M chuyển động trên cung BC thì chu vi tam giác APQ có giá trị không đổi.
Hướng dẫn giải
Hình vẽ minh họa:
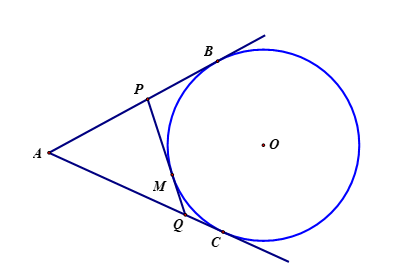
Ta có chu vi \(\Delta APQ\) bằng AP + PQ + QA và PQ = PM + MQ nên chu vi \(\Delta
APQ\) bằng AP + PM + MQ + QA (1)
Mặt khác ta có: PB = PM và QC = QM (2) (tính chất của hai tiếp tuyến cắt nhau)
Từ (1) và (2) ta có :
AP + PM + MQ + QA = AP + PB + QC + QA = AB + AC
Vậy chu vi \(\Delta APQ\) bằng AB + AC không đổi.
Bài tập 3. Cho nửa đường tròn \((O;R)\) đường kính \(AB\). Gọi \(M\) là điểm bất kì thuộc nửa đường tròn, kẻ \(MH\) vuông góc với \(AB\) (\(H\) thuộc \(AB)\). Vẽ đường tròn tâm \(M\) bán kính \(MH\). Kẻ các tiếp tuyến \(AC\), \(BD\) với đường tròn tâm \(M\) (\(C\), \(D\) là các tiếp điểm).
a) Chứng minh ba điểm \(C\), \(M\), \(D\) thẳng hàng và \(CD\) là tiếp tuyến của \((O)\).
b) Chứng minh rằng khi \(M\) di chuyển trên nửa đường tròn \((O)\) thì \(AC + BD\) không đổi.
Hướng dẫn giải
Hình vẽ minh họa:
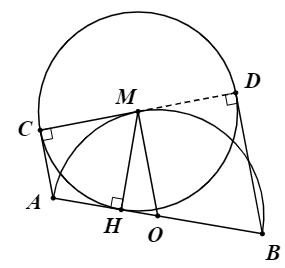
a) Ta có \(AC\), \(AH\) là tiếp tuyến của đường tròn \((M;MH)\) nên \(AM\) là phân giác của góc \(\widehat{CMH}\) hay \(\widehat{CMA} = \widehat{AMH}\)
Chứng minh tương tự có \(\widehat{HMB} =
\widehat{BMD}\)
Mà \(\widehat{AMH} + \widehat{HMB} =
\widehat{AMB} = 90^{\circ}\) (\(AB\) là đường kính)
\(\Rightarrow \widehat{CMA} + \widehat{AMH} +
\widehat{HMB} + \widehat{BMD} = 180^{\circ}\) Hay ba điểm \(C\), \(M\), \(D\) thẳng hàng
\(\Rightarrow CA//BD(\bot CD)\) hay tứ giác \(ABDC\) là hình thang vuông có \(OM\) là đường trung bình nên \(OM//AC\) và \(BD
\Rightarrow OM\bot CD\). Chứng tỏ \(CD\) là tiếp tuyến của (O).
b) Ta có \(AC = AH\), \(BD = BH\) (tính chất tiếp tuyến cắt nhau) \(\Rightarrow AC + BD = AH + BH = AB =
2R\) không đổi.
----------------------------------------------------
Qua chuyên đề chứng minh biểu thức không đổi khi điểm M di chuyển trên đường tròn, bạn đã được củng cố kiến thức về quỹ tích, hệ thức lượng và cách vận dụng đại số – hình học trong cùng một bài toán.
