Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 89.000đ

Bài tập trắc nghiệm Toán 12 Cánh Diều Bài 2 (Mức độ Vừa)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Thông hiểu
    Tìm giá trị nhỏ nhất của hàm số trên khoảng

    Tính giá trị nhỏ nhất của hàm số y = 3x + \frac{4}{x^{2}} trên khoảng (0; + \infty).

    Hướng dẫn:

    Cách 1:

    y = 3x + \frac{4}{x^{2}} = \frac{3x}{2} + \frac{3x}{2} + \frac{4}{x^{2}} \geq 3\sqrt[3]{\frac{3x}{2}.\frac{3x}{2}.\frac{4}{x^{2}}} = 3\sqrt[3]{9}

    Dấu " = " xảy ra khi \frac{3x}{2} = \frac{4}{x^{2}} \Leftrightarrow x = \sqrt[3]{\frac{8}{3}}.

    Vậy \min_{(0; + \infty)}y = 3\sqrt[3]{9}

    Cách 2:

    Xét hàm số y = 3x + \frac{4}{x^{2}} trên khoảng (0; + \infty)

    Ta có y = 3x + \frac{4}{x^{2}} \Rightarrow y' = 3 - \frac{8}{x^{3}}

    Cho y' = 0 \Leftrightarrow \frac{8}{x^{3}} = 3 \Leftrightarrow x^{3} = \frac{8}{3} \Leftrightarrow x = \sqrt[3]{\frac{8}{3}}

    \Rightarrow \min_{(0; + \infty)}y = y\left( \sqrt[3]{\frac{8}{3}} ight) = 3\sqrt[3]{9}

  • Câu 2: Thông hiểu
    Chọn mệnh đề đúng

    Cho hàm số f(x) = \frac{\sqrt{x^{2} - 1}}{x - 2} với x thuộc D = ( - \infty;\ - 1\rbrack \cup \left\lbrack 1;\ \frac{3}{2} \right\rbrack. Mệnh đề nào dưới đây đúng?

    Hướng dẫn:

    Hàm số xác định và liên tục trên D = ( - \infty;\ - 1brack \cup \left\lbrack 1;\ \frac{3}{2} ightbrack.

    f'(x) = \frac{- 2x + 1}{(x - 2)^{2}\sqrt{x^{2} - 1}}; f'(x) = 0 \Leftrightarrow x = \frac{1}{2} otin D

    Vậy \max_{D}f(x) = 0; \min_{D}f(x) = -\sqrt{5}.

  • Câu 3: Thông hiểu
    Chọn mệnh đề đúng

    Cho hàm số f(x) có đạo hàm trên \mathbb{R}. Đồ thị của hàm số y = f'(x) trên đoạn \lbrack - 2;2brack là đường cong hình bên. Mệnh đề nào dưới đây đúng?

    Hướng dẫn:

    Dựa vào thị của hàm số y = f^{'}(x) trên đoạn \lbrack - 2;2brack ta thấy f'(x) = 0\Leftrightarrow x = 1.

    Ta có bảng BBT:

    Do đó \max_{\lbrack - 2;2brack}f(x) =f(1).

  • Câu 4: Thông hiểu
    Giá trị nhỏ nhất của hàm số

    Cho hàm số y = f(x) liên tục trên và có bảng biến thiên như hình vẽ.

    Giá trị nhỏ nhất của hàm số

    Biết f(-4) > f(8), khi đó giá trị nhỏ nhất của hàm số đã cho trên bằng:

    Hướng dẫn:

    Từ bảng biến thiên ta có:

    \begin{matrix} f\left( x ight) \geqslant f\left( { - 4} ight),\forall x \in \left( { - \infty ;0} ight] \hfill \\ f\left( x ight) \geqslant f\left( 8 ight),\forall x \in \left( { - \infty ;0} ight) \hfill \\ \end{matrix}

    Mặt khác f(-4) > f(8) => \forall x \in \left( { - \infty ; + \infty } ight) thì f\left( x ight) \geqslant f\left( 8 ight)

    Vậy \mathop {\min }\limits_\mathbb{R} f\left( x ight) = f\left( 8 ight)

  • Câu 5: Nhận biết
    Chọn giá trị nhỏ nhất của hàm số trên đoạn

    Giá trị nhỏ nhất của hàm số y = x^{3} - 3x + 4 trên đoạn \lbrack 0;2brack là:

    Hướng dẫn:

    Ta có: y' = 3x^{2} - 3 = 0 \Leftrightarrow x = \pm 1

    Lại có: \left\{ \begin{matrix} f(0) = 4 \\ f(1) = 2 \\ f(2) = 6 \\ \end{matrix} ight.\ \Rightarrow \min_{\lbrack 0;2brack}y = 2

  • Câu 6: Thông hiểu
    Chọn phương án đúng

    Giá trị nhỏ nhất của hàm số y = x + \frac{2}{x} - \left( 1 + \sqrt{2} \right)^{2} trên khoảng (0; + \infty)

    Hướng dẫn:

    Hàm số xác định và liên tục trên khoảng (0; + \infty).

    y' = 1 - \frac{2}{x^{2}} = \frac{x^{2} - 2}{x^{2}}.

    y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = \sqrt{2} \\ x = - \sqrt{2} \\ \end{matrix} ight.\ .

    Bảng biến thiên:

    Vậy \min_{(0; + \infty)}y = f\left( \sqrt{2} ight) = - 3.

  • Câu 7: Thông hiểu
    Tính tổng min max của hàm số trên đoạn cho trước

    Cho hàm số y = f(x) liên tục và có đồ thị trên đoạn \lbrack - 2;\ 4brack như hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên đoạn \lbrack - 2;\ 4brack bằng

    Hướng dẫn:

    Dựa vào đồ thị hàm số ta có

    m = \underset{x \in \lbrack - 2\ ;\ 4brack}{Min}f(x) = - 4, M = \underset{x \in \lbrack - 2\ ;\ 4brack}{Max}f(x) = 7

    Khi đó M + m = 3

  • Câu 8: Thông hiểu
    Xác định min max của hàm số trên đoạn

    Cho hàm số y = f(x) xác định và liên tục trên \mathbb{R}, có đồ thị như hình vẽ bên.

    Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f(x) trên đoạn \lbrack - 2;2brack.

    Hướng dẫn:

    Nhận thấy trên đoạn \lbrack - 2;2brack

    Đồ thị hàm số có điểm thấp nhất có tọa độ ( - 2; - 5) và (1; - 5)

    \overset{}{ightarrow} Giá trị nhỏ nhất của hàm số này trên đoạn \lbrack - 2;2brack bằng - 5.

    Đồ thị hàm số có điểm cao nhất có tọa độ ( - 1; - 1) và (2; - 1)

    \overset{}{ightarrow} Giá trị lớn nhất của hàm số này trên đoạn \lbrack - 2;2brack bằng - 1.

  • Câu 9: Thông hiểu
    Ghi đáp án vào ô trống

    Sau khi phát hiện một dịch bệnh, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là f(t) = 35t^{2} - \frac{5}{3}t^{3} (kết quả khào sát trong 12 tháng liên tục). Nếu xem f^{'}(t) là tốc độ truyền bệnh (người/ngày) tại thời điểm t thì tốc độ truyền bệnh lớn nhất vào ngày thứ mấy?

    Trả lời: Ngày thứ 7

    Đáp án là:

    Sau khi phát hiện một dịch bệnh, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là f(t) = 35t^{2} - \frac{5}{3}t^{3} (kết quả khào sát trong 12 tháng liên tục). Nếu xem f^{'}(t) là tốc độ truyền bệnh (người/ngày) tại thời điểm t thì tốc độ truyền bệnh lớn nhất vào ngày thứ mấy?

    Trả lời: Ngày thứ 7

    Ta có f(t) = 35t^{2} - \frac{5}{3}t^{3} \Rightarrow f'(t) = 70t - 5t^{2}(t > 0)

    Vì f^{'}(t) có đồ thị là một parabol có bề lõm quay xuống nên đạt giá trị cực đại tại t = - \frac{70}{2( - 5)} = 7.

    Vậy vào ngày thứ 7 tốc độ truyền bệnh là nhanh nhất.

  • Câu 10: Thông hiểu
    Tìm GTLN của hàm số f(x)

    Giá trị lớn nhất của hàm số y = - {x^3} + 3x + 1 trên khoảng \left( {0; + \infty } ight)

    Hướng dẫn:

    Ta có:

    \begin{matrix} y' = - 3{x^2} + 3 \hfill \\ y' = 0 \Rightarrow \left[ {\begin{array}{*{20}{c}} {x = 1\left( {tm} ight)} \\ {x = - 1\left( L ight)} \end{array}} ight. \hfill \\ \end{matrix}

    => Giá trị lớn nhất của hàm số trên khoảng đã cho bằng 3 khi x = 1

  • Câu 11: Nhận biết
    Tính giá trị của biểu thức

    Cho hàm số y = f(x) liên tục trên đoạn \lbrack - 1;1brack và có đồ thị như hình vẽ.

    Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \lbrack - 1;1brack. Giá trị của M - m bằng:

    Hướng dẫn:

    Từ đồ thị ta thấy M = 1,\ m = 0 nên M - m = 1.

  • Câu 12: Thông hiểu
    Chọn đáp án thích hợp

    Độ giảm huyết áp của một bệnh nhân G(x) = 0,025x^{2}(30 - x) trong đó x là số miligam thuộc được tiêm cho bệnh nhân (0 < x < 30). Để bệnh nhân đó có huyết áp giảm nhiều nhất thì liều lượng thuốc cần tiêm vào là:

    Hướng dẫn:

    Ta có: G(x) = 0,025x^{2}(30 - x) \Rightarrow G'(x) = 1,5x - 0,075x^{2}

    \Rightarrow G'(x) = 0 \Leftrightarrow 1,5x - 0,075x^{2} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 20 \\ \end{matrix} ight.

    Ta có bảng biến thiên như sau:

    Vậy để bệnh nhân đó có huyết áp giảm nhiều nhất thì lượng thuốc cần tiêm vào là x = 20(mg).

  • Câu 13: Thông hiểu
    Tìm giá trị nhỏ nhất của hàm số

    Cho hàm số y = \frac{x^{2} - 4x}{2x + 1}. Tính giá trị nhỏ nhất của hàm số đã cho trên đoạn \lbrack 0;3brack?

    Hướng dẫn:

    Hàm số y = \frac{x^{2} - 4x}{2x + 1} liên tục trên đoạn \lbrack 0;3brack

    Ta có: y' = \frac{2x^{2} + 2x - 4}{(2x + 1)^{2}} \Rightarrow y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 2 \\ \end{matrix} ight.

    Khi đó \left\{ \begin{matrix} f(0) = 0 \\ f(1) = - 1 \\ f(3) = - \frac{3}{7} \\ \end{matrix} ight.\ \Rightarrow f(1) < f(3) < f(0) nên \min_{\lbrack 0;3brack}y = y(1) = - 1.

  • Câu 14: Nhận biết
    Chọn phương án đúng

    Cho hàm số y = f(x) xác định, liên tục trên\left\lbrack - 1,\frac{5}{2} \right\rbrackvà có đồ thị là đường cong như hình vẽ.

    Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f(x) trên \left\lbrack - 1,\frac{5}{2} \right\rbrack là:

    Hướng dẫn:

    Dựa vào đồ thị M = 4,\ \ m = - 1.

  • Câu 15: Thông hiểu
    Xác định tích các giá trị của m

    Cho hàm số y = \frac{x - m^{2}}{x + 2} với m là tham số. Tích tất cả các giá trị của tham số m để giá trị lớn nhất của hàm số đã cho trên đoạn \lbrack - 1;1brack bằng \frac{1}{4} bằng:

    Hướng dẫn:

    Ta có: y' = \frac{2 + m^{2}}{(x + 2)^{2}} > 0;\forall x \in \lbrack - 1;1brack

    \Rightarrow \max_{\lbrack - 1;1brack}y = y(1) = \frac{1 - m^{2}}{3} = \frac{1}{4} \Leftrightarrow m = \pm \frac{1}{2}

    Vậy tích tất cả các giá trị của tham số m bằng - \frac{1}{4}.

  • Câu 16: Thông hiểu
    Chọn mệnh đề đúng

    Mệnh đề nào sau đây là đúng về hàm số y = \frac{x + 1}{\sqrt{x^{2} + 5}}trên tập xác định của nó.

    Hướng dẫn:

    Tập xác định: D\mathbb{= R}.

    y' = \dfrac{\sqrt{x^{2} + 5} - (x + 1)\dfrac{2x}{2\sqrt{x^{2} + 5}}}{x^{2} + 5}

    = \frac{x^{2} + 5 - x^{2} - x}{\sqrt{x^{2} + 5}\left( x^{2} + 5 ight)} = \frac{5 - x}{\sqrt{x^{2} + 5}\left( x^{2} + 5 ight)}.

    y' = 0 \Leftrightarrow \frac{5 - x}{\sqrt{x^{2} + 5}\left( x^{2} + 5 ight)} = 0

    \Leftrightarrow 5 - x = 0 \Leftrightarrow x = 5

    Bảng biến thiên:

    Từ bảng biến thiên có \max_{\mathbb{R}}y = y(5) = \frac{\sqrt{30}}{5} khi x = 5.

    Hàm số y = \frac{x + 1}{\sqrt{x^{2} + 5}} không có giá trị nhỏ nhất.

    Vậy hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất.

  • Câu 17: Nhận biết
    Tìm giá trị nhỏ nhất của hàm số trên đoạn

    Giá trị nhỏ nhất của hàm số y = \frac{x^{3} - 3x}{x + 1} trên đoạn \lbrack 0;2brack bằng:

    Hướng dẫn:

    Ta có: y' = \frac{x^{2} + 2x - 3}{(x + 1)^{2}}

    \Rightarrow y' = 0 \Leftrightarrow \frac{x^{2} + 2x - 3}{(x + 1)^{2}} = 0

    \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 3 \\ \end{matrix} ight.. Khi đó \left\{ \begin{matrix}y(0) = 0 \\y(2) = - \dfrac{2}{3} \\y(1) = - 1 \\\end{matrix} ight.\ \Rightarrow \min_{\lbrack 0;2brack}y = y(1) = -1.

  • Câu 18: Thông hiểu
    Xét tính đúng sai của các nhận định

    Cho hàm số f(x) = 2x^{2} + \frac{500}{x}. Xét tính đúng sai của các mệnh đề sau

    a) f'(x) = 0 \Leftrightarrow x = 5. Đúng||Sai

    b) \lim_{x \rightarrow + \infty}f(x) = 0. Sai||Đúng

    b) Giá trị nhỏ nhất của hàm số trên (0;5) là 150. Sai||Đúng

    c) Giá trị nhỏ nhất của hàm số trên (0; + \infty) là 150. Đúng||Sai

    Đáp án là:

    Cho hàm số f(x) = 2x^{2} + \frac{500}{x}. Xét tính đúng sai của các mệnh đề sau

    a) f'(x) = 0 \Leftrightarrow x = 5. Đúng||Sai

    b) \lim_{x \rightarrow + \infty}f(x) = 0. Sai||Đúng

    b) Giá trị nhỏ nhất của hàm số trên (0;5) là 150. Sai||Đúng

    c) Giá trị nhỏ nhất của hàm số trên (0; + \infty) là 150. Đúng||Sai

    a) Đúng

    b) Sai

    c) Sai

    d) Đúng

    Ta có:

    f'(x) = 4x - \frac{500}{x^{2}} = \frac{4x^{3} - 500}{x^{2}}

    f'(x) = 0 \Leftrightarrow 4x^{3} - 500 = 0 \Leftrightarrow x = 5.

    Bảng biến thiên.

    .

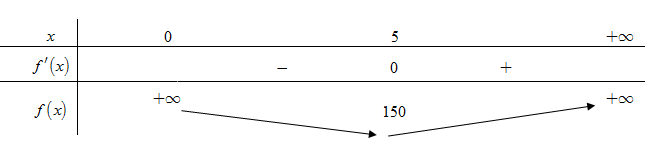    Vậy giá trị nhỏ nhất của hàm số trên khoảng (0; + \infty) là 150 khi x = 5.

  • Câu 19: Thông hiểu
    Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số

    Cho hàm số y = f(x) xác định và liên tục trên \mathbb{R} có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f(x) trên đoạn \lbrack - 2\ ;\ 2brack.

    Hướng dẫn:

    Nhìn vào đồ thị ta thấy:

    M = \max_{\lbrack - 2\ ;\ 2brack}f(x) = - 1 khi x = - 1 hoặc x = 2.

    m = \min_{\lbrack - 2\ ;\ 2brack}f(x) = - 5 khi x = - 2 hoặc x = 1.

  • Câu 20: Vận dụng
    Tìm số thực m thỏa mãn điều kiện

    Tìm giá trị thực của tham số m để hàm số f(x) = -x3 – 3x2 + m có giá trị nhỏ nhất trên đoạn [-1; 1] bằng 0.

    Hướng dẫn:

    Xét hàm số f(x) = -x3 – 3x2 + m trên đoạn [-1; 1] ta có:

    f’(x) = -3x2 – 6x

    f’(x) = 0 => \left\{ {\begin{array}{*{20}{c}} { - 1 \leqslant x \leqslant 1} \\ { - 3{x^2} - 6x = 0} \end{array}} ight. \Leftrightarrow x = 0

    Ta tính được

    \begin{matrix} \left\{ {\begin{array}{*{20}{c}} {f\left( { - 1} ight) = 2 + m} \\ \begin{gathered} f\left( 0 ight) = m \hfill \\ f\left( 1 ight) = - 4 + m \hfill \\ \end{gathered} \end{array}} ight. \Rightarrow \mathop {\min }\limits_{\left[ { - 1;1} ight]} f\left( x ight) = f\left( 1 ight) = - 4 + m \hfill \\ \Leftrightarrow \mathop {\min }\limits_{\left[ { - 1;1} ight]} f\left( x ight) = 0 \Rightarrow m = 4 \hfill \\ \end{matrix}

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (20%):
    2/3
  • Thông hiểu (75%):
    2/3
  • Vận dụng (5%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Tải file làm trên giấy
1
38 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này