Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Trắc nghiệm Toán 12 Kết nối tri thức
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 89.000đ

Bài tập trắc nghiệm Toán 12 KNTT Bài 5 (Mức độ Dễ)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Nhận biết
    Tính tốc độ nhỏ nhất của xe đua

    Đồ thị bên dưới là tốc độ của một chiếc xe đua trên đoạn đường đua bằng phẳng dài 3 km.

    Tốc độ nhỏ nhất của xe đua trên đoạn đường này bằng

    Hướng dẫn:

    Dựa vào đồ thị ta thấy tốc độ nhỏ nhất bằng \mathbf{70}\mathbf{km}\mathbf{/}\mathbf{h}.

  • Câu 2: Nhận biết
    Chọn phương án thích hợp

    Mực nước biển trung bình tại trường sa từ năm 2013 đến năm 2019 được cho bởi biểu đồ trong hình bên dưới.

    Trong khoảng thời gian từ năm 2016 đến năm 2019, năm nào mực nước biển trung bình tại trường sa cao nhất ?

    Hướng dẫn:

    Nhìn vào biểu đồ ta thấy, tại năm 2018 mực nước biển trung bình tại trường sa cao nhất bằng 242\ mm.

  • Câu 3: Nhận biết
    Chọn kết luận đúng

    Hình bên cho biết sự thay đổi của nhiệt độ ở một thành phố trong một ngày. Thời điểm nào trong ngày có nhiệt độ thấp nhất ?

    Hướng dẫn:

    Từ đồ thị ta thấy thời điểm có nhiệt độ thấp nhất trong ngày là vào 4h sáng.

  • Câu 4: Nhận biết
    Tìm vận tốc tức thời của vật

    Một vật rơi tự do có phương trình chuyển động là s(t) = \frac{1}{2}gt^{2}, trong đó g = 9,8m/s^{2}. Tìm vận tốc tức thời của vật tại thời điểm t = 3(s).

    Hướng dẫn:

    Ta có: v(t) = s'(t) = 9,8t.

    Vận tốc tức thời của vật tại thời điểm t = 3(s)là: v(3) = 9,8.3 = 29,4(m/s).

  • Câu 5: Nhận biết
    Tìm vận tốc tức thời của vật

    Một vật rơi tự do có phương trình chuyển động là s(t) = \frac{1}{2}gt^{2}, trong đó g = 9,8m/s^{2}. Tìm thời điểm mà vận tốc tức thời của vật tại thời điểm đó bằng 39,2(m/s).

    Hướng dẫn:

    Thật vậy: v(t) = s'(t) = 9,8t.

    Ta có: v(t) = 9,8t = 39,2 \Leftrightarrow t = 4.

    Vậy vận tốc tức thời của vật đạt 39,2(m/s) tại thời điểm t = 4(s).

  • Câu 6: Thông hiểu
    Xét tính đúng sai của các nhận định

    Dân số của một quốc gia sau t bắt đầu từ năm 2023 được tính theo công thức N(t) = 100e^{0,012t} . Các khẳng định dưới đây đúng hay sai?

    a) Dân số của quốc gia này ở năm 2030 vượt mức 110 triệu người. Sai||Đúng

    b) Dân số của quốc gia này ở năm 2035 vượt mức 115 triệu người. Đúng||Sai

    c) Vào năm 2030 thì tốc độ tăng dân số là 1,6 triệu người/năm. Sai||Đúng

    d) Vào năm 2026 thì tốc độ tăng dân số là 1,6 triệu người/năm. Đúng||Sai

    Đáp án là:

    Dân số của một quốc gia sau t bắt đầu từ năm 2023 được tính theo công thức N(t) = 100e^{0,012t} . Các khẳng định dưới đây đúng hay sai?

    a) Dân số của quốc gia này ở năm 2030 vượt mức 110 triệu người. Sai||Đúng

    b) Dân số của quốc gia này ở năm 2035 vượt mức 115 triệu người. Đúng||Sai

    c) Vào năm 2030 thì tốc độ tăng dân số là 1,6 triệu người/năm. Sai||Đúng

    d) Vào năm 2026 thì tốc độ tăng dân số là 1,6 triệu người/năm. Đúng||Sai

    a) Sai

    b) Đúng

    c) Sai

    d) Đúng

    a) Dân số của quốc gia này ở năm 2030 là N(7) = 100e^{0,012.7} \approx 108,8 triệu người.

    b) Dân số của quốc gia này ở năm 2035 là N(12) = 100e^{0,012.12} \approx 115,5 triệu người.

    c) Hàm tốc độ tăng dân số là N'(t) = 1,2e^{0,012t}. Ta có:

    1,2e^{0,012t} = 1,6 \Leftrightarrow t \approx 2,34.

    Vậy thời vào năm 2026, tốc độ tăng dân số là 1,6 triệu người/năm

    d) Hàm tốc độ tăng dân số là N'(t) = 1,2e^{0,012t}. Ta có:

    1,2e^{0,012t} = 1,6 \Leftrightarrow t \approx 2,34.

    Vậy thời vào năm 2026, tốc độ tăng dân số là 1,6 triệu người/năm.

  • Câu 7: Nhận biết
    Xét tính đúng sai của các nhận định

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    A diagram of a mathematical equationDescription automatically generated

    Mỗi khẳng định sau đây đúng hay sai?

    a) Hàm số y = f(x) đồng biến trên khoảng ( - \infty;2). Sai||Đúng

    b) Hàm số y = f(x)nghịch biến trên khoảng (0;3). Đúng||Sai

    c) Hàm số y = f(x)đạt cực đại tại x = 2. Sai||Đúng

    d) Giá trị cực tiểu của hàm số y = f(x) là y = - 4. Đúng||Sai

    Đáp án là:

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    A diagram of a mathematical equationDescription automatically generated

    Mỗi khẳng định sau đây đúng hay sai?

    a) Hàm số y = f(x) đồng biến trên khoảng ( - \infty;2). Sai||Đúng

    b) Hàm số y = f(x)nghịch biến trên khoảng (0;3). Đúng||Sai

    c) Hàm số y = f(x)đạt cực đại tại x = 2. Sai||Đúng

    d) Giá trị cực tiểu của hàm số y = f(x) là y = - 4. Đúng||Sai

    a) Sai

    b) Đúng

    c) Sai

    d) Đúng

    a) Hàm số y = f(x) đồng biến trên các khoảng ( - \infty;0) và (3; + \infty).

    b) Hàm số y = f(x) nghịch biến trên khoảng (0;3).

    c) Hàm số y = f(x)đạt cực đại tại x = 0.

    d) Giá trị cực tiểu của hàm số y = f(x) là y = - 4.

  • Câu 8: Thông hiểu
    Tính thời gian số vi khuẩn đạt max

    Một loại vi khuẩn được tiêm một loại thuốc kích thích sự sinh sản. Sau t phút, số vi khuẩn được xác định theo công thức N(t) = 1000 + 30t^{2} - t^{3}\ (0 \leq t \leq 30). Hỏi sau bao giây thì số vi khuẩn lớn nhất?

    Hướng dẫn:

    Xét hàm số N(t) = 1000 + 30t^{2} - t^{3}\ (0 \leq t \leq 30).

    N'(t) = 60t - 3t^{2}.

    N'(t) = 0 \Leftrightarrow \left\lbrack \begin{matrix} t = 0 \\ t = 20 \\ \end{matrix} \right..

    Description: A picture containing chartDescription automatically generated

    Với t = 20 giây thì số vi khuẩn lớn nhất.

  • Câu 9: Thông hiểu
    Xét tính đúng sai của các nhận định

    Cho hàm số bậc ba y = f(x) có đồ thị là đường cong như hình vẽ sau

    Mỗi khẳng định sau đây đúng hay sai?

    a) Hàm số y = f(x) đồng biến trên khoảng ( - \infty;3).Đúng||Sai

    b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số y = f(x) là 2. Sai||Đúng

    c) Hàm số y = f(x)có hai cực trị trái dấu. Sai||Đúng

    d) Phương trình đường thẳng qua 2 điểm cực trị của đồ thị hàm số y = f(x) là d:y = - 3x. Đúng||Sai

    Đáp án là:

    Cho hàm số bậc ba y = f(x) có đồ thị là đường cong như hình vẽ sau

    Mỗi khẳng định sau đây đúng hay sai?

    a) Hàm số y = f(x) đồng biến trên khoảng ( - \infty;3).Đúng||Sai

    b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số y = f(x) là 2. Sai||Đúng

    c) Hàm số y = f(x)có hai cực trị trái dấu. Sai||Đúng

    d) Phương trình đường thẳng qua 2 điểm cực trị của đồ thị hàm số y = f(x) là d:y = - 3x. Đúng||Sai

    a) Sai

    b) Đúng

    c) Đúng

    d) Sai

    a) Hàm số y = f(x) đồng biến trên các khoảng ( - \infty; - 1) và (1; + \infty).

    b) Giá trị cực đại là y = 3, giá trị cực tiểu là y = –1. Do đó tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho là 3 - 1 = 2.

    c) Hàm số y = f(x) có hai cực trị là x = \pm 1.

    d) Gọi d:y = ax + b là đường thẳng qua hai điểm cực trị A( - 1;3),B(1; - 1).

    A,B \in d \Rightarrow \left\{\begin{matrix}- a + b = 3 \\a + b = - 1\end{matrix} \right.\Rightarrow \left\{ \begin{matrix}a = - 2 \\b = 1\end{matrix} \right.\ \Rightarrow d:y = - 2x + 1

  • Câu 10: Thông hiểu
    Tính tốc độ tăng trưởng của dân số

    Dân số P (tính theo nghìn người) của một thành phố nhỏ được cho bởi công thức P(t) = \frac{500t}{t^{2} + 9}, trong đó t là thời gian được tính bằng năm. Tìm tốc độ tăng dân số tại thời điểm t = 12.

    Hướng dẫn:

    Tốc độ tăng trưởng dân số là:

    P'(t) = \frac{(500t)^{'}\left( t^{2} + 9 \right) - 500t\left( t^{2} + 9 \right)^{'}}{\left( t^{2} + 9 \right)^{2}}

    P'(t) = \frac{500.\left( t^{2} + 9 \right) - 500t.2t}{\left( t^{2} + 9 \right)^{2}}

    P'(t) = \frac{4500 - 500t^{2}}{\left( t^{2} + 9 \right)^{2}}

    Khi t\ = 12 thì

    P'(12) = \frac{4500 - 500.12^{2}}{\left( 12^{2} + 9 \right)^{2}} = - 2,88

  • Câu 11: Nhận biết
    Xét tính đúng sai của các nhận định

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    A diagram of a mathematical equationDescription automatically generated

    Xét tính đúng sai của các nhận định dưới đây?

    a) Hàm số y = f(x) đồng biến trên khoảng ( - \infty;2). Sai||Đúng

    b) Hàm số y = f(x)nghịch biến trên khoảng (0;3). Đúng||Sai

    c) Hàm số y = f(x)đạt cực đại tại x = 2. Sai||Đúng

    d) Giá trị cực tiểu của hàm số y = f(x) là y = - 4. Đúng||Sai

    Đáp án là:

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    A diagram of a mathematical equationDescription automatically generated

    Xét tính đúng sai của các nhận định dưới đây?

    a) Hàm số y = f(x) đồng biến trên khoảng ( - \infty;2). Sai||Đúng

    b) Hàm số y = f(x)nghịch biến trên khoảng (0;3). Đúng||Sai

    c) Hàm số y = f(x)đạt cực đại tại x = 2. Sai||Đúng

    d) Giá trị cực tiểu của hàm số y = f(x) là y = - 4. Đúng||Sai

    a) Sai

    b) Đúng

    c) Sai

    d) Đúng

    a) Hàm số y = f(x) đồng biến trên các khoảng ( - \infty;0) và (3; + \infty).

    b) Hàm số y = f(x) nghịch biến trên khoảng (0;3).

    c) Hàm số y = f(x)đạt cực đại tại x = 0.

    d) Giá trị cực tiểu của hàm số y = f(x) là y = - 4.

  • Câu 12: Nhận biết
    Tính vận tốc tức thời của chuyển động

    Một chuyển động thẳng xác định bởi phương trình s(t) = 4t^{3} + 6t + 2, trong đó s tính bằng mét và t là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại t = 2.

    Hướng dẫn:

    Vận tốc tức thời của chuyển động là:v(t) = s'(t) = 12t^{2} + 6

    Khi t = 2,\ v(2) = 12.2^{2} + 6 = 54(m/s)

  • Câu 13: Thông hiểu
    Chọn đáp án đúng

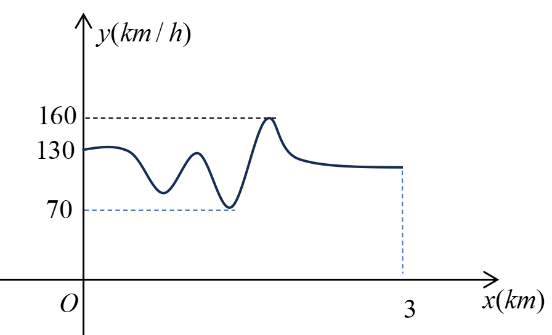
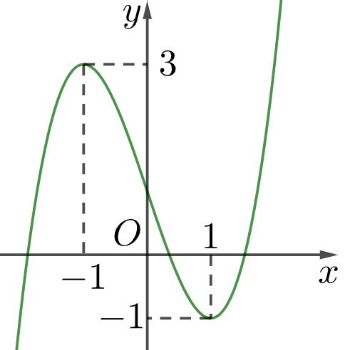
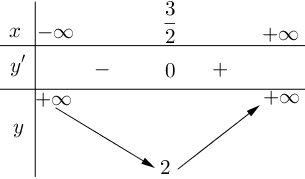
    Một viên đạn được bắn lên cao theo phương thẳng đứng có phương trình chuyển động s(t) = 2 + 196t - 4,9t^{2}, trong đó t \geq 0, t(s) là thời gian chuyển động, s(m) là độ cao so với mặt đất. Tại thời điểm viên đạn đạt vận tốc tức thời bằng 98\ m/sthì viên đạn đang ở độ cao bao nhiêu mét so với mặt đất?

    Hướng dẫn:

    Viên đạn đạt vận tốc tức thời bằng 98\ m/s ta có phương trình: 

    v(t) = 196 - 9,8t = 98 \Leftrightarrow t = 10

    Khi đó viên đạn đang ở độ cao là:

    s(10) = 2 + 196.10 - 4,9.10^{2} = 1472(m).

  • Câu 14: Nhận biết
    Tính vận tốc tức thời của chất điểm

    Một chất điểm chuyển động của phương trình s(t) = \frac{1}{3}t^{3} - 2t^{2} + 4t + 1 trong đó t > 0, ttính bằng giây, s(t)tính bằng mét. Tính vận tốc tức thời của chất điểm tại thời điểm t = 3(s).

    Hướng dẫn:

    Vận tốc tức thời của chất điểm tại thời điểm t(s)là: v(t) = s'(t) = t^{2} - 4t + 4.

    Vậy vận tốc tức thời của chất điểm tại thời điểm t = 3(s)là: v(3) = 3^{2} - 4.3 + 4 = 1(m/s)

  • Câu 15: Thông hiểu
    Xác định vận tốc của vật khi chạm đất

    Một vật được phóng theo phương thẳng đứng lên trên từ mặt đất với vận tốc ban đầu là 19,6m/s thì độ cao h của nó (tính bằng m) sau t giây được cho bởi công thức h = 19,6t - 4,9t^{2}. Tìm vận tốc của vật khi nó chạm đất.

    Hướng dẫn:

    Tại thời điểm mà vật đạt độ cao bằng 0, ta có: 0 = 19,6t - 4,9t^{2} \Leftrightarrow 0 = t(19,6 - 4,9t) \Leftrightarrow \left\lbrack \begin{matrix} t = 0 \\ t = 4 \\ \end{matrix} \right.

    Khi t = 4 (thời điểm vật chạm đất), ta có:19,6 - 9,8(4) = - 19,6.

    Vậy vận tốc của vật khi nó chạm đất là 19,6 m/s.

  • Câu 16: Nhận biết
    Tính lợi nhuận cao nhất của doanh nghiệp

    Một doanh nghiệp dự kiến lợi nhuận khi sản xuất x sản phẩm (0 \leq x \leq 300) được cho bởi hàm số y = - x^{3} + 300x^{2} và được minh họa bằng đồ thị ở hình bên dưới.

    Cần sản xuất bao nhiêu sản phẩm để doanh nghiệp thu được lợi nhuận cao nhất?

    Hướng dẫn:

    Dựa vào đồ thị ta thấy hàm số có giá trị lớn nhất bằng 4000000 khi x = 200

    Do đó cần sản suất 200 sản phẩm thì doanh nghiệp thu được lợi nhuận cao nhất.

  • Câu 17: Thông hiểu
    Xác định hàm số v(t)

    Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250\ km so với bể mặt của Mặt Trăng. Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao h của con tàu so với bề mặt của Mặt Trăng được tính (gẩn đúng) bởi hàm h(t) = - 0,01t^{3} + 1,1t^{2} - 30t + 250, trong đó t là thời gian tính bằng giây và h là độ cao tính bằng kilômét. Gọi v(t) là vận tốc tức thời của con tàu ở thời điểm t (giây) kể từ khi đốt cháy các tên lửa hãm với 0 \leq t \leq 50. Xác định hàm số v(t).

    Hướng dẫn:

    Vận tốc tức thời của con tàu ở thời điểm t, v(t), là đạo hàm của hàm số h(t) theo thời gian t. Hàm số h(t) đã cho là: h(t) = - 0,01t^{3} + 1,1t^{2} - 30t + 250

    Để tìm v(t), ta lấy đạo hàm của h(t): v(t) = h^{'}(t) = - 0,03t^{2} + 2,2t - 30

    Vậy hàm số v(t)biểu diễn vận tốc tức thời của con tàu ở thời điểm t là:

    v(t) = - 0,03t^{2} + 2,2t - 30

  • Câu 18: Nhận biết
    Chọn đáp án đúng

    Hình bên cho biết lượng mưa trung bình các tháng năm 2019 tại Thành phố Hồ Chí Minh đo theo đơn vị milimet. Hãy cho biết vào tháng nào trong năm 2019 thì lượng mưa là cao nhất ?

    ANH3

    Hướng dẫn:

    Từ đồ thị ta thấy vào Tháng 9 thì lượng mưa ở Thành phố Hồ Chí Minh cao nhất trong năm 2019

  • Câu 19: Nhận biết
    Xét tính đúng sai của các nhận định

    Cho đồ thị hàm số y = \frac{bx - c}{x - a} (a,b,c\mathbb{\in R}) có đồ thị như hình vẽ bên dưới.

    A graph of a functionDescription automatically generated

    Xét tính đúng sai của các nhận định?

    a) Hàm số nghịch biến trên từng khoảng xác định. Đúng||Sai

    b) Giao điểm với trục tung là điểm có tung độ âm. Đúng||Sai

    c) Giao điểm với trục hoành là điểm có hoành độ âm. Đúng||Sai

    d) Trong các số a,b,c có hai số âm. Sai||Đúng

    Đáp án là:

    Cho đồ thị hàm số y = \frac{bx - c}{x - a} (a,b,c\mathbb{\in R}) có đồ thị như hình vẽ bên dưới.

    A graph of a functionDescription automatically generated

    Xét tính đúng sai của các nhận định?

    a) Hàm số nghịch biến trên từng khoảng xác định. Đúng||Sai

    b) Giao điểm với trục tung là điểm có tung độ âm. Đúng||Sai

    c) Giao điểm với trục hoành là điểm có hoành độ âm. Đúng||Sai

    d) Trong các số a,b,c có hai số âm. Sai||Đúng

    a) Đúng

    b) Đúng

    c) Đúng

    d) Sai

    a) Đúng.

    Hàm số nghịch biến trên từng khoảng xác định.

    b) Đúng.

    Giao điểm với trục tung là điểm có tung độ âm.

    c) Đúng.

    Giao điểm với trục hoành là điểm có hoành độ âm.

    d) Sai.

    Tiệm cận đứng x = a > 0.

    Tiệm cận ngang y = b > 0.

    Đồ thị hàm số cắt trục tung tại điểm có tung độ \frac{c}{a} < 0 \Rightarrow c < 0 .

  • Câu 20: Nhận biết
    Tìm vận tốc tức thời của chuyển động

    Một vật chuyển động có quãng đường được xác định bởi phương trình s(t) = 2t^{2} + 5t + 2, trong đó s tính bằng mét và t là thời gian tính bằng giây. Tính vận tốc tức thời tại thời điểm t = 4.

    Hướng dẫn:

    Ta có s'(t) = 4t + 5,s'(4) = 21m/s

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (65%):
    2/3
  • Thông hiểu (35%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Tải file làm trên giấy
1
52 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này