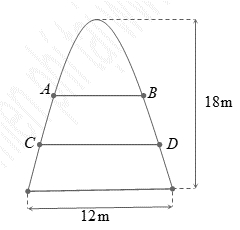
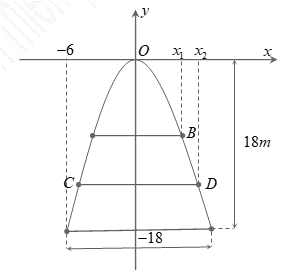
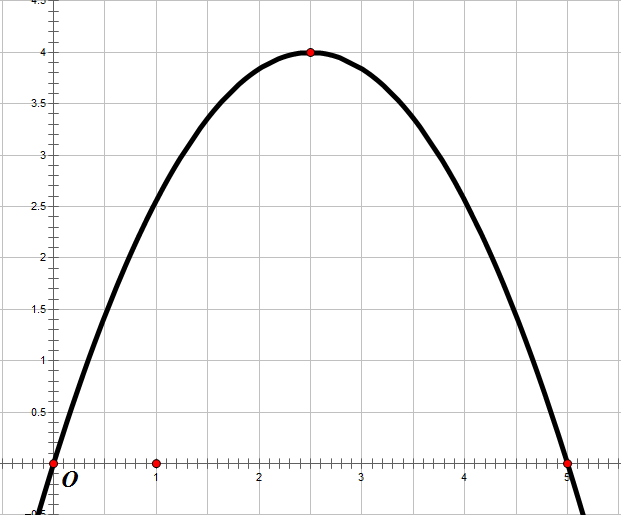
Mặt sàn của một thang máy có dạng hình vuông ABCD cạnh 2m được lát gạch màu trắng và trang trí vởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ tọa độ Oxy với là tâm hình vuông sao cho
như hình vẽ bên thì các đường cong OA có phương trình
và
. Tính giá trị
biết rằng diện tích trang trí màu sẫm chiếm
diện tích mặt sàn.
Đáp án: -2||- 2
Mặt sàn của một thang máy có dạng hình vuông ABCD cạnh 2m được lát gạch màu trắng và trang trí vởi một hình 4 cánh giống nhau màu sẫm. Khi đặt trong hệ tọa độ Oxy với là tâm hình vuông sao cho
như hình vẽ bên thì các đường cong OA có phương trình
và
. Tính giá trị
biết rằng diện tích trang trí màu sẫm chiếm
diện tích mặt sàn.
Đáp án: -2||- 2
Diện tích 1 cánh của hình trang trí là:
Diện tích hình trang trí là:
Vì diện tích trang trí màu sẫm chiếm diện tích mặt sàn nên
Khi đó ta có:
Vậy .
 .
.