Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập trắc nghiệm Toán 12 Cánh Diều Bài 2 (Mức độ Khó)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Vận dụng
    Ghi đáp án vào ô trống

    Ông A dự định sử dụng hết 8\ \ m^{2} kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích lớn nhất bằng bao nhiêu m^{3}? (Kết quả làm tròn đến chữ số thập phân thứ nhất).

    Đáp án: 2,1

    Đáp án là:

    Ông A dự định sử dụng hết 8\ \ m^{2} kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng. Bể cá có dung tích lớn nhất bằng bao nhiêu m^{3}? (Kết quả làm tròn đến chữ số thập phân thứ nhất).

    Đáp án: 2,1

    Gọi x,h (m) lần lượt là chiều rộng và chiều cao của bể cá.

    Ta có thể tích bể cá V = 2x^{2}h.

    Theo đề bài ta có:

    2xh + 2.2xh + 2x^{2} = 8

    \Leftrightarrow 6xh + 2x^{2} = 8

    \Leftrightarrow h = \frac{8 - 2x^{2}}{6x}

    V = 2x^{2}\frac{8 - 2x^{2}}{6x} = \frac{8x - 2x^{3}}{3}

    \Rightarrow V' = \frac{8 - 6x^{2}}{3}

    \Rightarrow V' = 0

    \Leftrightarrow 8 - 6x^{2} = 0 \Leftrightarrow x^{2} = \frac{4}{3} \Leftrightarrow x = \frac{2\sqrt{3}}{3}

    Ta có bảng biển thiên

    \Rightarrow V_{\max} = \frac{32\sqrt{3}}{27} \approx 2,1\ \ m^{3}

  • Câu 2: Thông hiểu
    Xác định vận tốc của chuyển động

    Vận tốc của một chất điểm được xác định bởi công thức v(t) = t^{3} - 10t^{2} + 29t - 20 (với v được tính bằng giây). Vận tốc của chất điểm tại thời điểm gia tốc nhỏ nhất gần bằng:

    Hướng dẫn:

    Gia tốc của chất điểm a(t) = v'(t) = 3t^{2} - 20t + 29 gia tốc là hàm số bậc hai ẩn t đạt giá trị nhỏ nhất tại t = \frac{10}{3}

    Tại đó, vận tốc của chất điểm bằng v\left( \frac{10}{3} ight) = \frac{70}{27} \approx 2,59.

  • Câu 3: Vận dụng
    Chọn mệnh đề đúng

    Cho hàm số y = \frac{x + m}{x - 1} thỏa mãn \min_{\lbrack 2;4brack}y = 3. Chọn mệnh đề đúng?

    Hướng dẫn:

    Tập xác định D\mathbb{= R}\backslash\left\{ 1 ight\}

    Ta có: y' = \frac{- 1 - m}{(x - 1)^{2}}. Vì hàm số đơn điệu trên \lbrack 2;4brack nên

    \left[ \begin{gathered} \mathop {\min }\limits_{\left[ {2;4} ight]} y = y\left( 2 ight); - 1 - m > 0 \hfill \\ \mathop {\min }\limits_{\left[ {2;4} ight]} y = y\left( 4 ight); - 1 - m < 0 \hfill \\ \end{gathered} ight.\mathop \to \limits^{\mathop {\min }\limits_{\left[ {2;4} ight]} y = 3} \left[ \begin{gathered} 3 = 2 + m;m < - 1 \hfill \\ 3 = \dfrac{{4 + m}}{3};m > - 1 \hfill \\ \end{gathered} ight.

    \Leftrightarrow \left\lbrack \begin{matrix} m = 1;m < - 1 \\ m = 5;m > - 1 \\ \end{matrix} ight.\ \Leftrightarrow m = 5

    Nếu m = - 1 ightarrow y = 1 Hàm số không có giá trị lớn nhất

    Vậy m > 4

  • Câu 4: Thông hiểu
    Chọn đáp án đúng

    Một chất điểm chuyển động với vận tốc được cho bởi công thức v(t) = - t^{2} + 4t + 2 với t (giây) là khoảng thời gian tính từ khi chất điểm bắt đầu chuyển động. Hỏi tại thời điểm nào thì vận tốc của chất điểm là lớn nhất?

    Hướng dẫn:

    Ta có: v(t) = - t^{2} + 4t + 2 với t > 0.

    v'(t) = - 2t + 4

    v'(t) = 0 \Leftrightarrow - 2t + 4 = 0 \Leftrightarrow t = 2 (thỏa mãn).

    Bảng biến thiên

    Dựa vào bảng biến thiên, tại thời điểm t = 2 giây thì vận tốc của chất điểm là lớn nhất.

  • Câu 5: Thông hiểu
    Tìm m thỏa mãn bất phương trình

    Tìm giá trị của m để bất phương trình x + \frac{4}{x - 1} \geq m có nghiệm trên khoảng ( - \infty;1)?

    Hướng dẫn:

    Bất phương trình x + \frac{4}{x - 1} \geq m có nghiệm trên khoảng ( - \infty;1)

    \Leftrightarrow m \leq \max_{( - \infty;1brack}g(x)

    Với g(x) = x + \frac{4}{x - 1} \Rightarrow g'(x) = 1 - \frac{4}{(x - 1)^{2}}

    g'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 3 otin ( - \infty;1) \\ x = - 1 \in ( - \infty;1) \\ \end{matrix} ight.

    Ta có bảng biến thiên

    Dựa vào bảng biến thiên ta suy ra m \leq - 3.

  • Câu 6: Vận dụng cao
    Tìm min và max của hàm số

    Cho hai số thực x, y thỏa mãn x \geqslant 0;y \geqslant 0 và x + y = 1. Giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P = \frac{x}{{y + 1}} + \frac{y}{{x + 1}} lần lượt là:

    Hướng dẫn:

    Ta có: 

    P = \frac{x}{{y + 1}} + \frac{y}{{x + 1}} = \frac{{x\left( {x + 1} ight) + y\left( {y + 1} ight)}}{{\left( {x + 1} ight)\left( {y + 1} ight)}} = \frac{{{{\left( {x + y} ight)}^2} - 2xy + 1}}{{xy + x + y + 1}} = \frac{{2 - 2xy}}{{2 + xy}}

    Đặt t = xy ta được P = \frac{{2 - 2t}}{{2 + t}}

    Vì x \geqslant 0;y \geqslant 0 \Rightarrow t \geqslant 0

    Mặt khác 1 = x + y \geqslant 2\sqrt {xy} \Leftrightarrow xy \leqslant \frac{1}{4} \Rightarrow t \leqslant \frac{1}{4}

    Khi đó bài toán trở thành tìm giá trị lớn nhất của hàm số g\left( t ight) = \frac{{2 - 2t}}{{2 + t}} trên \left[ {0;\frac{1}{4}} ight]

    Xét hàm số g\left( t ight) = \frac{{2 - 2t}}{{2 + t}} xác định và liên tục trên \left[ {0;\frac{1}{4}} ight]

    Ta có: g'\left( t ight) = \frac{{ - 6}}{{{{\left( {2 + t} ight)}^2}}} < 0,\forall t \in \left( {0;\frac{1}{4}} ight)

    => Hàm số g(t) nghịch biến trên đoạn \left[ {0;\frac{1}{4}} ight]

    => \left\{ {\begin{array}{*{20}{c}} {\mathop {\min }\limits_{\left[ {0;\frac{1}{4}} ight]} g\left( t ight) = g\left( {\dfrac{1}{4}} ight) = \dfrac{2}{3}} \\ {\mathop {\max }\limits_{\left[ {0;\frac{1}{4}} ight]} g\left( t ight) = g\left( 0 ight) = 1} \end{array}} ight.

  • Câu 7: Vận dụng
    Xác định m thỏa mãn yêu cầu đề bài

    Cho hàm số y = f(x) có bảng biến thiên trên đoạn \lbrack - 4;4brack như hình vẽ:

    Có bao nhiêu giá trị của tham số m trên đoạn \lbrack - 4;4brack sao cho giá trị lớn nhất của hàm số y = f\left( \left| x^{3} ight| + 3|x| ight) + f(m) trên đoạn \lbrack - 1;1brack bằng 1?

    Hướng dẫn:

    Ta có: x \in \lbrack - 1;1brack \Rightarrow |x| \in \lbrack 0;1brack \Rightarrow \left| x^{3} ight| \in \lbrack 0;1brack

    Suy ra t = \left| x^{3} ight| + 3|x| \in \lbrack 0;4brack

    Khi đó f\left( \left| x^{3} ight| + 3|x| ight) \in \lbrack - 3;3brack hay f\left( \left| x^{3} ight| + 3|x| ight) + f(m) \in \left\lbrack - 3 + f(m);3 + f(m) ightbrack

    Theo yêu cầu bài toán \Leftrightarrow 3 + f(m) = 1 \Leftrightarrow f(m) = - 2

    Nhìn vào bảng biến thiên ta thấy f(m) = - 2 có ba nghiệm

    Vậy có 3 giá trị của tham số m thỏa mãn yêu cầu bài toán.

  • Câu 8: Vận dụng
    Định giá trị m thỏa mãn bất phương trình

    Cho hàm số f(x) có đạo hàm trên \mathbb{R} và thỏa mãn f(x) > f'(x) + 1;\forall x\mathbb{\in R}. Bất phương trình f(x) < me^{x} + 1 nghiệm đúng với mọi x \in (0; + \infty) khi và chỉ khi

    Hướng dẫn:

    Ta có:

    f(x) < me^{x} + 1 \Leftrightarrow f(x) - 1 < me^{x}

    \Leftrightarrow \frac{f(x) - 1}{e^{x}} < m.

    Xét hàm số g(x) = \frac{f(x) - 1}{e^{x}} có

    g'(x) = \frac{f'(x) - \left\lbrack f(x) - 1 ightbrack}{e^{x}} < 0;\forall x \in (0; + \infty)

    Bảng biến thiên

    Vậy bất phương trình f(x) < me^{x} + 1 nghiệm đúng với mọi x \in (0; + \infty) khi và chỉ khi m \geq f(0) - 1.

  • Câu 9: Vận dụng cao
    Xác định số phần tử của tập hợp

    Gọi K là tập hợp các giá trị nguyên của tham số m \in \left[ {0;2019} ight] để bất phương trình {x^2} - m + \sqrt {{{\left( {1 - {x^2}} ight)}^3}} \leqslant 0 nghiệm đúng với mọi x \in \left[ { - 1;1} ight] . Số các phần tử của tập hợp K là:

    Hướng dẫn:

    Đặt t = \sqrt {1 - {x^2}} ;x \in \left[ { - 1;1} ight] \Rightarrow t \in \left[ {0;1} ight]

    Bất phương trình đã cho trở thành {t^3} - {t^2} + 1 - m \leqslant 0 \Leftrightarrow m \geqslant {t^3} - {t^2} + 1\left( * ight)

    Yêu cầu bài toán tương đương với bất phương trình (*) nghiệm đúng với mọi t \in \left[ {0;1} ight]

    Xét hàm số f\left( t ight) = {t^3} - {t^2} + 1 \Rightarrow f'\left( t ight) = 3{t^3} - 2t

    f'\left( t ight) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {t = 0\left( L ight)} \\ {t = \dfrac{2}{3}\left( {tm} ight)} \end{array}} ight.

    Vì \left\{ {\begin{array}{*{20}{c}} {f\left( 0 ight) = f\left( 1 ight) = 1} \\ {f\left( {\dfrac{2}{3}} ight) = \dfrac{{23}}{{27}}} \end{array}} ight. \Rightarrow \mathop {\max }\limits_{\left[ {0;1} ight]} f\left( t ight) = 1

    Do đó bất phương trình (*) nghiệm đúng với mọi t \in \left[ {0;1} ight] khi và chỉ khi m \geqslant 1

    Mặt khác m là số nguyên thuộc [0; 2019] nên m \in \left\{ {1;2;3;...;2019} ight\}

  • Câu 10: Vận dụng
    Xét tính đúng sai của các mệnh đề sau

    Cho hàm số y = f(x) liên tục và có bảng biến thiên trong đoạn \lbrack - 1;3brack như hình.

    Các mệnh đề sau đúng hay sai?

    a) [NB] Trên \lbrack - 1;3brack hàm số y = f(x) có 2 điểm cực trị. Đúng||Sai

    b) [TH] Giá trị lớn nhất của hàm số y = f(x) trên đoạn \lbrack - 1;3brack là 6. Sai|||Đúng

    c) [TH] Tổng của giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn \lbrack - 1;3brackbằng 6. Đúng||Sai

    d) [VD] Hàm số g(x) = f(4 - x) có đạt giá trị nhỏ nhất và giá trị lớn nhất trên đoạn \lbrack 1;3brack lần lượt bằng a\ và\ b. Khi đó giá trị của a^{2} + b^{2} = 53. Đúng||Sai

    Đáp án là:

    Cho hàm số y = f(x) liên tục và có bảng biến thiên trong đoạn \lbrack - 1;3brack như hình.

    Các mệnh đề sau đúng hay sai?

    a) [NB] Trên \lbrack - 1;3brack hàm số y = f(x) có 2 điểm cực trị. Đúng||Sai

    b) [TH] Giá trị lớn nhất của hàm số y = f(x) trên đoạn \lbrack - 1;3brack là 6. Sai|||Đúng

    c) [TH] Tổng của giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn \lbrack - 1;3brackbằng 6. Đúng||Sai

    d) [VD] Hàm số g(x) = f(4 - x) có đạt giá trị nhỏ nhất và giá trị lớn nhất trên đoạn \lbrack 1;3brack lần lượt bằng a\ và\ b. Khi đó giá trị của a^{2} + b^{2} = 53. Đúng||Sai

    a) Đúng.

    Trên \lbrack - 1;3brack hàm số y = f(x) đạt cực trị tại x\ = \ 0;\ x\ = \ 2.

    b) Sai.

    Giá trị lớn nhất của hàm số y = f(x) trên đoạn \lbrack - 1;3brack là 7 khi x = 3. Mệnh đề sai.

    c) Đúng.

    Tổng của giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn \lbrack - 1;3brack bằng - 1 + 7\ = 6. Mệnh đề đúng.

    d) Đúng.

    Xét Hàm số g(x) = f(4 - x) trên đoạn \lbrack 1;3brack.

    Ta có g'(x) = - f'(4 - x)

    g'(x) = 0 \Leftrightarrow f'(4 - x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} 4 - x = 0 \\ 4 - x = 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x = 4 otin \lbrack 1;3brack \\ x = 2 \in \lbrack 1;3brack \\ \end{matrix} ight.

    Ta có;

    g(1) = f(3) = 7;g(2) = f(2) = 2;2 < g(3) = f(1) < 7

    Do đó y = g(x) đạt giá trị nhỏ nhất và giá trị lớn nhất trên đoạn \lbrack 1;3brack bằng 2 và 7.

    Hay a = 2,b = 7. Khi đó giá trị của a^{2} + b^{2} = 53. Mệnh đề đúng.

  • Câu 11: Thông hiểu
    Xét tính đúng sai của các nhận định

    Cho hàm số y = x^{3} - 3x + 2. Khi đó nhận định nào đúng, nhận định nào sai?

    a) Tập xác định của hàm số đã cho là (0\ ;\ + \infty). Sai||Đúng

    b) Đồ thị của hàm số đã cho đi qua điểm (0\ ;2). Đúng||Sai

    c) Hàm số đạt cực trị tại x = 0. Sai||Đúng

    d) Giá trị lớn nhất của hàm số đã cho trên đoạn \lbrack 0;2\rbrack bằng 4. Đúng||Sai

    Đáp án là:

    Cho hàm số y = x^{3} - 3x + 2. Khi đó nhận định nào đúng, nhận định nào sai?

    a) Tập xác định của hàm số đã cho là (0\ ;\ + \infty). Sai||Đúng

    b) Đồ thị của hàm số đã cho đi qua điểm (0\ ;2). Đúng||Sai

    c) Hàm số đạt cực trị tại x = 0. Sai||Đúng

    d) Giá trị lớn nhất của hàm số đã cho trên đoạn \lbrack 0;2\rbrack bằng 4. Đúng||Sai

    a) Sai

    b) Đúng

    c) Sai

    d) Đúng

    a) SAI vì Tập xác định của hàm số đã cho là \mathbb{R}.

    b) ĐÚNG. Thay x = 0 ta được y = 2.

    c) SAI. Ta có y' = 3x^{2} - 3. Ta thấy y'(0) = - 3 \neq 0. Suy ra hàm số không đạt cực trị tại điểm x = 0.

    d) ĐÚNG. Ta có y' = 3x^{2} - 3.Suy ra y' = 0 \Leftrightarrow x = 1\ (TM);x = - 1\ (KTM).

    y(0) = 2;y(2) = 4;y(1) = 0. Vậy giá trị lớn nhất của hàm số đã cho trên đoạn \lbrack 0;2\rbrack bằng 4.

  • Câu 12: Vận dụng cao
    Tính tổng GTLN và GTNN của hàm số

    Cho hàm số f(x) liên tục trên khoảng (0; +∞) thỏa mãn 3x.f\left( x ight) - {x^2}.f'\left( x ight) = 2{f^2}\left( x ight), với f(x) ≠ 0 với ∀x ∈ (0; +∞) và f\left( 1 ight) = \frac{1}{3}. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [1;2]. Tính tổng M + m.

    Hướng dẫn:

    Ta có:

    \begin{matrix} 3x.f\left( x ight) - {x^2}.f'\left( x ight) = 2{f^2}\left( x ight) \hfill \\ \Rightarrow 3{x^2}f\left( x ight) - {x^3}f'\left( x ight) = 2x{f^2}\left( x ight) \hfill \\ \Rightarrow \dfrac{{3{x^2}f\left( x ight) - {x^3}f'\left( x ight)}}{{{f^2}\left( x ight)}} = 2x \hfill \\ \Rightarrow \left( {\dfrac{{{x^3}}}{{f\left( x ight)}}} ight)' = 2x \Rightarrow \dfrac{{{x^3}}}{{f\left( x ight)}} = {x^2} + C \hfill \\ \end{matrix}

    Thay x = 1 vào ta có: \left\{ {\begin{array}{*{20}{c}} {\dfrac{1}{{f\left( 1 ight)}} = 1 + C} \\ {f\left( 1 ight) = \dfrac{1}{3}} \end{array}} ight. \Rightarrow C = 2

    \begin{matrix} \Rightarrow f\left( x ight) = \dfrac{{{x^3}}}{{{x^2} + 2}} \hfill \\ f'\left( x ight) = \dfrac{{{x^4} + 6{x^2}}}{{{{\left( {{x^2} + 2} ight)}^2}}} \hfill \\ f'\left( x ight) = 0 \Rightarrow x = 0 \hfill \\ \end{matrix}

    Ta có bảng biến thiên

    Tính tổng GTLN và GTNN của hàm số

    Khi đó f(x) đồng biến trên [1; 2]

    => \left\{ {\begin{array}{*{20}{c}} {m = f\left( 1 ight) = \dfrac{1}{3}} \\ {M = f\left( 2 ight) = \dfrac{4}{3}} \end{array}} ight. \Rightarrow m + M = \dfrac{5}{3}

  • Câu 13: Vận dụng
    Tìm điều kiện để hàm số đạt giá trị lớn nhất trên khoảng

    Cho hàm số y = f(x) xác định và liên tục trên [-2; 2], có đồ thị của hàm số y f’(x) như hình vẽ sau:

    Tìm điều kiện để hàm số đạt giá trị lớn nhất trên khoảng

    Tìm giá trị của x0 để hàm số y = f(x) đạt giá trị lớn nhất trên [-2; 2]

    Hướng dẫn:

     Từ đồ thị ta có: f’(x) = 0 => \left[ {\begin{array}{*{20}{c}} {x = - 1} \\ {x = 1} \end{array}} ight.

    Ta có bảng biến thiên như sau:

    Tìm điều kiện để hàm số đạt giá trị lớn nhất trên khoảng

    Từ bảng biến thiên ta có x0 = 1 thỏa mãn điều kiện

  • Câu 14: Vận dụng cao
    Tính GTNN của biểu thức

    Cho x, y là các số thực thỏa mãn {\left( {x - 3} ight)^2} + {\left( {y - 1} ight)^2} = 5. Giá trị nhỏ nhất của biểu thức P = \frac{{3{y^2} + 4xy + 7x + 4y - 1}}{{x + 2y + 1}} bằng:

    Hướng dẫn:

    \begin{matrix} {\left( {x - 3} ight)^2} + {\left( {y - 1} ight)^2} = 5 \hfill \\ \Rightarrow {x^2} + {y^2} - 6x - 2y + 5 = 0 \hfill \\ P = \dfrac{{\left( {3{y^2} + 4xy + 7x - 4y - 1} ight) + \left( {{x^2} + {y^2} - 6x - 2y + 5} ight)}}{{x + 2y + 1}} \hfill \\ P = \dfrac{{4{y^2} + 4xy + {x^2} + x + 2y + 4}}{{x + 2y + 1}} \hfill \\ P = \dfrac{{{{\left( {2y + x} ight)}^2} + \left( {x + 2y} ight) + 4}}{{x + 2y + 1}} \hfill \\ \end{matrix}

    Đặt t = x + 2y

    \begin{matrix} \left( {{1^2} + {2^2}} ight)\left[ {{{\left( {x - 3} ight)}^2} + {{\left( {y - 1} ight)}^2}} ight] \geqslant {\left[ {\left( {x - 3} ight) + \left( {2y - 2} ight)} ight]^2} \hfill \\ \Rightarrow {\left( {x + 2y - 5} ight)^2} \leqslant 25 \hfill \\ \Leftrightarrow 0 \leqslant x + 2y \leqslant 10 \hfill \\ \end{matrix}

    Ta được P = f\left( t ight) = \frac{{{t^2} + t + 4}}{{1 + 4}} = t + \frac{4}{{t + 1}};0 \leqslant t \leqslant 10

    Xét f'\left( t ight) = 1 - \frac{4}{{{{\left( {t + 1} ight)}^2}}} = 0 \Rightarrow {\left( {t + 1} ight)^2} = 4 \Rightarrow \left[ {\begin{array}{*{20}{c}} {t = 1\left( {tm} ight)} \\ {t = - 3\left( L ight)} \end{array}} ight.

    Vì f\left( 0 ight) = 4;f\left( {10} ight) = \frac{{114}}{{11}};f\left( 1 ight) = 3 \Rightarrow \min P = 3{\text{ khi t = 1}}

  • Câu 15: Thông hiểu
    Ghi đáp án đúng vào ô trống

    Cho hàm số y = e^{x}\left( x^{2} - 3 \right), gọi M = \frac{a}{e^{b}}\left( a\mathbb{\in N},b\mathbb{\in N} \right) là giá trị lớn nhất của hàm số trên đoạn \lbrack - 5; - 2\rbrack. Tính giá trị của biểu thức P = a + b?

    Đáp án: 9

    Đáp án là:

    Cho hàm số y = e^{x}\left( x^{2} - 3 \right), gọi M = \frac{a}{e^{b}}\left( a\mathbb{\in N},b\mathbb{\in N} \right) là giá trị lớn nhất của hàm số trên đoạn \lbrack - 5; - 2\rbrack. Tính giá trị của biểu thức P = a + b?

    Đáp án: 9

    Ta có: y' = e^{x}\left( x^{2} + 2x - 3 ight) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 3 \in \lbrack - 5; - 2brack \\ x = 1 otin \lbrack - 5; - 2brack \\ \end{matrix} ight.

    Ta có y( - 5) = \frac{22}{e^{5}};y( - 3) = \frac{6}{e^{3}};y( - 2) = \frac{1}{e^{2}}.

    Khi đó \max_{\lbrack - 5; - 2brack}y = \frac{6}{e^{3}} \Rightarrow a = 6;b = 3 \Rightarrow a + b = 9.

  • Câu 16: Vận dụng cao
    Tìm số phần tử của tập hợp S

    Cho hàm số f(x) = x^{3} - 3x^{2} + m^{2} - 2m với m là tham số. Gọi S tập hợp tất cả các giá trị nguyên của tham số m thỏa mãn 3\max_{\lbrack - 3;1brack}f\left( |x| ight) + 2\min_{\lbrack - 3;1brack}f\left( |x| ight) \leq 112. Số phần tử của tập hợp S bằng:

    Hướng dẫn:

    Ta có: f\left( |x| ight) = f\left( | - x| ight);\forall x\mathbb{\in R}

    \Rightarrow \left\{ \begin{matrix} \max_{\lbrack - 3;1brack}f\left( |x| ight) = \max_{0;3}f(x) \\ \min_{\lbrack - 3;1brack}f\left( |x| ight) = \min_{\lbrack 0;3brack}f(x) \\ \end{matrix} ight.

    Đạo hàm f'(x) = 3x^{2} - 6x = 0

    \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \Rightarrow f(0) = m^{2} - 2m \\ x = 2 \Rightarrow f(2) = m^{2} - 2m - 4 \\ \end{matrix} ight. và f(3) = m^{2} - 2m

    Suy ra 3\max_{\lbrack - 3;1brack}f\left( |x| ight) + 2\min_{\lbrack - 3;1brack}f\left( |x| ight) \leq 112

    \Leftrightarrow 3\left( m^{2} - 2m ight) + 2\left( m^{2} - 2m - 4 ight) \leq 112

    \Leftrightarrow m^{2} - 2m - 24 \leq 0 \Leftrightarrow - 4 \leq m \leq 6

    Mà m\mathbb{\in Z \Rightarrow}m \in \left\{ - 4; - 3;...;5;6 ight\}

    Vậy có tất cả 11 giá trị nguyên của tham số m.

  • Câu 17: Thông hiểu
    Ghi đáp án vào ô trống

    Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật s(t) = t^{3} - 4t^{2} + 12(m), trong đó t(s) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc của chất điểm đó đạt giá trị bé nhất khi t bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Một chất điểm chuyển động thẳng với quãng đường biến thiên theo thời gian bởi quy luật s(t) = t^{3} - 4t^{2} + 12(m), trong đó t(s) là khoảng thời gian tính từ lúc bắt đầu chuyển động. Vận tốc của chất điểm đó đạt giá trị bé nhất khi t bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 18: Thông hiểu
    Chọn đáp án đúng

    Cho hàm số y = f(x) có đồ thị như hình vẽ sau:

    Khi đó, giá trị lớn nhất của hàm số g(x) = f\left( 2 - x^{2} ight) trên \left\lbrack 0;\sqrt{2} ightbrack là:

    Hướng dẫn:

    Đặt t = 2 - x^{2};t' = - 2x \leq 0;\forall x \in \left\lbrack 0;\sqrt{2} ightbrack \Rightarrow t \in \lbrack 0;2brack

    \Rightarrow \max_{\left\lbrack 0;\sqrt{2} ightbrack}g(x) = \max_{\lbrack 0;2brack}f(t) = f(0)

  • Câu 19: Vận dụng
    Ghi đáp án vào ô trống

    Gọi S là tập các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số là f\left( x ight) = \left| {\frac{1}{4}{x^4} - 14{x^2} + 48x + m - 30} ight| trên đoạn [0; 2] không vượt quá 30. Tổng các phần tử của S bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Gọi S là tập các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số là f\left( x ight) = \left| {\frac{1}{4}{x^4} - 14{x^2} + 48x + m - 30} ight| trên đoạn [0; 2] không vượt quá 30. Tổng các phần tử của S bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 20: Vận dụng
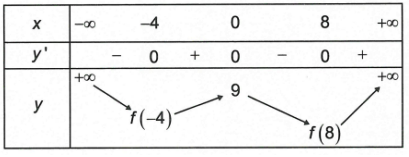
    Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

    Cho hàm số f(x) có đạo hàm f’(x). Đồ thị của hàm số y = f’(x) được biểu diễn trong hình vẽ dưới đây.

    Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

    Biết rằng f\left( 0 ight) + f\left( 1 ight) + f\left( 3 ight) = f\left( 4 ight) + 2f\left( 2 ight). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số f(x) trên đoạn [0; 4]?

    Hướng dẫn:

    Ta có bảng xét dấu như sau:

    Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

    Dựa vào bảng xét dấy ta có M = f(2), GTNN chỉ có thể là f(0) hoặc f(4)

    Ta lại có

    f(1) và f(3) nhỏ hơn f(2) => f(1) + f(3) < 2f(2)

    => 2f(2) – f(1) – f(3) > 0

    Theo bài ra ta có:

    f(0) + f(1) + f(3) = f(4) + 2f(2)

    => f(0) – f(4) = 2f(2) – f(1) – f(3) > 0

    => f(0) – f(4) > 0 => f(0) > f(4)

    => GTNN đạt được tại x = 4

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (35%):
    2/3
  • Thông hiểu (40%):
    2/3
  • Vận dụng (25%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
1
17 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Lớp 12
Xem thêm