Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Trắc nghiệm Toán 12 Ứng dụng hình học của Tích phân (Mức Vừa)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Thông hiểu
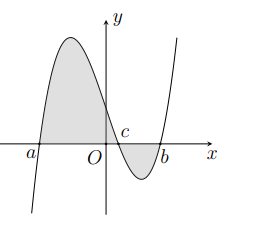
    Tính diện tích hình phẳng

    Cho hàm số f(x) = x^{3} - 3x^{2} + 2x. Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục tung, trục hoành và đường thẳng x = 3

    Hướng dẫn:

    Ta có:

    S = \int_{0}^{1}\left| x^{3} - 3x^{2} + 2x ight|dx

    = \int_{0}^{3}{\left( x^{3} - 3x^{2} + 2x ight)dx} - \int_{1}^{2}{\left( x^{3} - 3x^{2} + 2x ight)dx}

    + \int_{2}^{3}{\left( x^{3} - 3x^{2} + 2x ight)dx}

    = \frac{1}{4} + \frac{1}{4} + \frac{9}{4} = \frac{11}{4}

  • Câu 2: Nhận biết
    Tính diện tích hình phẳng

    Diện tích hình phẳng giới hạn bởi các đường y = x^{3}, trục hoành, x = 1 và x = 3 bằng

    Hướng dẫn:

    Diện tích hình giới hạn là S = \int_{1}^{3}{\left| x^{3} ight|dx} = \left| \int_{3}^{3}{x^{3}dx} ight| = \left| \left. \ \left( \frac{x^{4}}{4} ight) ight|_{1}^{3} ight| = 20

  • Câu 3: Vận dụng
    Ghi đáp án đúng vào ô trống

    Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc, xây dựng, thiết bị nội thất,... Mặt trong (lọt lòng) và ngoài (phủ bì) của một bồn rửa (lavabo) bằng sứ có hình dạng là một nửa khối tròn xoay khi quay quanh một trục của 2 elip có chung các trục đối xứng (hình minh họa). Thông số kĩ thuật mặt trên của bồn rửa: dài x rộng là 660 \times 380mm (phủ bì) và elip (lọt lòng) có trục lớn, trục nhỏ ít hơn elip phủ bì một khoảng 40 mm. Tính thể tích chứa nước của bồn rửa (đơn vị: lít) (làm tròn kết quả đến hàng phần mười).

    Đáp án: 18,8

    Đáp án là:

    Hình elip được ứng dụng nhiều trong thực tiễn, đặc biệt là kiến trúc, xây dựng, thiết bị nội thất,... Mặt trong (lọt lòng) và ngoài (phủ bì) của một bồn rửa (lavabo) bằng sứ có hình dạng là một nửa khối tròn xoay khi quay quanh một trục của 2 elip có chung các trục đối xứng (hình minh họa). Thông số kĩ thuật mặt trên của bồn rửa: dài x rộng là 660 \times 380mm (phủ bì) và elip (lọt lòng) có trục lớn, trục nhỏ ít hơn elip phủ bì một khoảng 40 mm. Tính thể tích chứa nước của bồn rửa (đơn vị: lít) (làm tròn kết quả đến hàng phần mười).

    Đáp án: 18,8

    Chọn hệ trục tọa độ Oxy thích hợp với đơn vị trên trục là decimet.

    Phương trình elip lọt lòng: (E):\frac{x^{2}}{3,1^{2}} + \frac{y^{2}}{1,7^{2}} = 1 \Leftrightarrow y = \pm 1,7\sqrt{1 - \frac{x^{2}}{3,1^{2}}}.

    Thể tích chứa nước của bồn rửa: V = \frac{1}{2}.\pi\int_{- 3,1}^{3,1}{1,7^{2}\left( 1 - \frac{x^{2}}{3,1^{2}} ight)dx} \approx 18,8 lít.

  • Câu 4: Thông hiểu
    Tìm thể tích khối tròn xoay

    Tính thể tích khối tròn xoay sinh ra khi quay quanh trục Ox hình phẳng giới hạn bởi hai đồ thị y = x^{2} - 4x + 6;y = - x^{2} - 2x + 6?

    Hướng dẫn:

    Phương trình hoành độ giao điểm

    x^{2} - 4x + 6 = - x^{2} - 2x + 6 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 1 \\ \end{matrix} ight.

    Gọi (H) là hình phẳng giới hạn bởi các đường y = x^{2} - 4x + 6;y = - x^{2} - 2x + 6;x = 0;x = 1

    Thể tích khối tròn xoay tạo thành khi quay (H) quanh Ox l

    Diện tích hình phẳng là:

    V = \left| \pi\int_{0}^{1}{\left\lbrack \left( x^{2} - 4x + 6 ight)^{2} - \left( - x^{2} - 2x + 6 ight)^{2} ightbrack dx} ight|

    = \left| \pi\int_{0}^{1}{\left\lbrack \left( 2x^{2} - 12 ight)(12 - 6x) ightbrack dx} ight|

    = \left| \pi\int_{0}^{1}{\left( - 12x^{3} + 36x^{2} - 24x ight)dx} ight|

    = \left| \pi\left. \ \left( - 3x^{4} + 36x^{2} - 24x ight) ight|_{0}^{1} ight| = 3\pi

  • Câu 5: Thông hiểu
    Tính thể tích của vật thể

    Một vật thể nằm giữa hai mặt phẳng x = - 1;x = 1 và thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x;( - 1 \leq x \leq 1) là một hình tròn có diện tích bằng 3\pi. Thể tích của vật thể là?

    Hướng dẫn:

    Ta có: V = \int_{- 1}^{1}{S(x)dx} = \int_{- 1}^{1}{3\pi dx} = 6\pi

  • Câu 6: Vận dụng
    Tính diện tích nhỏ nhất

    Diện tích nhỏ nhất giới hạn bởi parabol (P):y = x^{2} + 1 và đường thẳng d:y = mx + 2 là:

    Hướng dẫn:

    Hoành độ giao điểm của đồ thị hai hàm số là nghiệm của phương trình

    x^{2} + 1 = mx + 2 \Leftrightarrow x^{2} - mx - 1 = 0

    Vì \Delta = m^{2} + 4 > 0;\forall m\mathbb{\in R} nên phương trình luôn có 2 nghiệm phân biệt

    x_{1} = \frac{m - \sqrt{m^{2} + 4}}{2};x_{2} = \frac{m + \sqrt{m^{2} + 4}}{2} với x_{1} < x_{2}

    Ta có: \left\{ \begin{matrix} x_{1} + x_{2} = m \\ x_{1}.x_{2} = - 1 \\ x_{2} - x_{1} = \sqrt{m^{2} + 4} \\ \end{matrix} ight..

    Diện tích hình phẳng giới hạn bởi (P) và (d) là:

    S = \int_{x_{1}}^{x_{2}}{\left| \left( x^{2} - mx - 1 ight) ight|dx}

    = \left| \int_{x_{1}}^{x_{2}}{\left( x^{2} - mx - 1 ight)dx} ight| = \left| \left. \ \left( \frac{x^{3}}{2} - \frac{mx^{2}}{2} - x ight) ight|_{x_{1}}^{x_{2}} ight|

    = \left| \frac{1}{3}\left( {x_{2}}^{3} - {x_{1}}^{3} ight) - \frac{m}{2}\left( {x_{2}}^{2} - {x_{1}}^{2} ight) - \left( x_{2} - x_{1} ight) ight|

    = \left( x_{2} - x_{1} ight)\left| \frac{1}{3}\left( {x_{2}}^{2} + x_{1}x_{2} + {x_{1}}^{2} ight) - \frac{m}{2}\left( x_{2} + x_{1} ight) - 1 ight|

    = \left( x_{2} - x_{1} ight)\left| \frac{1}{3}\left( x_{2} + x_{1} ight)^{2} - x_{2}x_{1} - \frac{m}{2}\left( x_{2} + x_{1} ight) - 1 ight|

    = \sqrt{m^{2} + 4}.\left| \frac{m^{2} + 1}{3} - \frac{m^{2}}{2} - 1 ight|

    = \sqrt{m^{2} + 4}.\left| \frac{m^{2}}{6} - \frac{2}{3} ight| = \sqrt{m^{2} + 4}.\frac{m^{2} + 4}{6} \geq \frac{4}{3};\forall m\mathbb{\in R}

    Vậy diện tích nhỏ nhất giới hạn bởi parabol (P):y = x^{2} + 1 và đường thẳng d:y = mx + 2 là \frac{4}{3}.

  • Câu 7: Vận dụng
    Tính thể tích quả bóng

    Một quả bóng bầu dục có khoảng cách giữa 2 điểm xa nhất bằng 10 cm và cắt quả bóng bằng mặt phẳng trung trực của đoạn thẳng đó thì được đường tròn có diện tích bằng 16\pi\left( \ cm^{2} ight). Thể tích của quả bóng bằng (Tính gần đúng đến hai chữ số thập phân, đơn vị lít)

    Gợi ý:

    Sử dụng phương trình chính tắc của Elip: \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1, với 2a là độ dài trục lớn, 2b là độ dài trục nhỏ.

    Hướng dẫn:

    Quả bóng bầu dục sẽ có dạng elip.

    Độ dài trục lớn bằng 20\ cm \Rightarrow2a = 20 \Rightarrow a = 5\ \ (cm)

    Ta có diện tích đường tròn thiết diện là

    S = \pi b^{2} = 16\pi \Rightarrow b =4(\ cm)

    Ta sẽ có phương trình elip \frac{x^{2}}{25} + \frac{y^{2}}{16} = 1

    \Rightarrow V = \pi\int_{- 5}^{5}{16\left( 1 - \frac{x^{2}}{25} ight)}dx \approx 335\ \ \left( \ cm^{3} ight) = 0,34\ (l).

  • Câu 8: Thông hiểu
    Tính diện tích hình phẳng

    Tính diện tích hình phẳng giới hạn bởi đồ thị (C) của hàm số y = - 2x^{3} + x^{2} + x + 5 và đồ thị (C') của hàm số y = x^{2} - x + 5?

    Hướng dẫn:

    Phương trình hoành độ giao điểm

    - 2x^{3} + x^{2} + x + 5 = x^{2} - x + 5

    \Leftrightarrow - 2x^{3} + 2x = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 1 \\ x = - 1 \\ \end{matrix} ight.

    Diện tích hình phẳng cần tìm là:

    S = \int_{- 1}^{1}{\left| 2x^{3} - 2x ight|dx}

    = \left| \int_{- 1}^{0}{\left( 2x^{3} - 2x ight)dx} ight| + \left| \int_{0}^{1}{\left( 2x^{3} - 2x ight)dx} ight|

    = 1

  • Câu 9: Thông hiểu
    Tìm diện tích hình phẳng

    Tính diện tích S của hình phẳng giới hạn bởi y = x^{2} - 2x, y = 0, x = - 4, x = 1.

    Hướng dẫn:

    Xét phương trình hoành độ giao điểm: x^{2} - 2x = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 2 \\ \end{matrix} \right..

    Diện tích: S = \int_{- 4}^{1}{\left| x^{2} - 2x \right|dx} = \int_{- 4}^{0}{\left( x^{2} - 2x \right)dx} - \int_{0}^{1}{\left( x^{2} - 2x \right)dx}

    = \left. \ \left( \frac{x^{3}}{3} - x^{2} \right) \right|_{- 4}^{0} - \left. \ \left( \frac{x^{3}}{3} - x^{2} \right) \right|_{0}^{1} = 38.

  • Câu 10: Thông hiểu
    Tính diện tích thiết diện

    Tính diện tích S của hình phẳng giới hạn bởi các đường y = e^{x};y = 2;x = 0;x = 1?

    Hướng dẫn:

    Phương trình hoành độ giao điểm e^{x} = 2 \Leftrightarrow x = ln2 \in (0;1)

    Do đó, diện tích hình phẳng giới hạn bởi các đường y = e^{x};y = 2;x = 0;x = 1

    S = \int_{0}^{1}{\left| e^{x} - 2 ight|dx}

    = - \int_{0}^{\ln2}{\left( e^{x} - 2ight)dx} + \int_{\ln2}^{1}{\left( e^{x} - 2 ight)dx}

    = - \left. \ \left( e^{x} - 2x ight)ight|_{0}^{\ln2} + \left. \ \left( e^{x} - 2x ight)ight|_{\ln2}^{1}

    = - (2 - 2\ln2 - 1) + (e - 2 - 2 +2\ln2)

    = 4\ln2 + e - 5

  • Câu 11: Thông hiểu
    Tính thể tích tròn xoay

    Tính thể tích của vật thể giới hạn bởi hai mặt phẳng x = 0;x = 3 biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x;(0 \leq x \leq 3) là hình chữ nhật có kích thước là x và 2\sqrt{9 - x^{2}}?

    Hướng dẫn:

    Thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ x;(0 \leq x \leq 3) là hình chữ nhật có kích thước là x và 2\sqrt{9 - x^{2}}

    Diện tích thiết diện được xác định theo hàm là: S(x) = 2x\sqrt{9 - x^{2}}

    ⇒ Thể tích vật thể tròn xoay: V = \int_{0}^{3}{2x\sqrt{9 - x^{2}}}dx = 18

  • Câu 12: Thông hiểu
    Chọn kết luận chính xác nhất

    Cho hình vẽ:

    Diện tích hình phẳng (phần gạch chéo) giới hạn bởi đồ thị 3 hàm số f(x);g(x);h(x) như hình bên, bằng kết quả nào sau đây?

    Hướng dẫn:

    Diện tích miền tích phân được chia thành hai phần. Phần 1 với x nằm trong khoảng a đến b và phần 2 với x nằm trong khoảng b đến c:

    S = \int_{a}^{b}{\left| f(x) - g(x) ight|dx} + \int_{b}^{c}{\left| g(x) - h(x) ight|dx}

    = \int_{a}^{b}{\left\lbrack f(x) - g(x) ightbrack dx} + \int_{b}^{c}{\left\lbrack h(x) - g(x) ightbrack dx}

    = \int_{a}^{b}{\left\lbrack f(x) - g(x) ightbrack dx} - \int_{b}^{c}{\left\lbrack g(x) - h(x) ightbrack dx}.

  • Câu 13: Thông hiểu
    Tính diện tích hình phẳng

    Diện tích hình phẳng giới hạn bởi nhánh đường cong y = x^{2} với x \geq 0, đường thẳng y = 2 - x và trục hoành bằng

    Hướng dẫn:

    Xét phương trình hoành độ giao điểm:

    x^{2} = 2 - x \Leftrightarrow x^{2} + x - 2 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 2(ktm) \\ \end{matrix} ight.

    Ta có \Rightarrow S = \int_{0}^{1}{\left| x^{2} - (2 - x) ight|d_{x}} = \frac{7}{6}

  • Câu 14: Thông hiểu
    Chọn công thức thích hợp

    Cho hai hàm số f(x) và g(x) liên tục trên \lbrack a;bbrack và thỏa mãn 0 < g(x) < f(x),\forall x \in \lbrack a;bbrack. Gọi V là thể tích của khối tròn xoay sinh ra khi quay quanh Ox hình phẳng (H) giới hạn bởi các đường: y = f(x),y = g(x),x = a,x = b. Khi đó V được tính bởi công thức nào sau đây?

    Hướng dẫn:

    Ta cần nhớ lại công thức sau: Cho hai hàm số y = f(x),y = g(x) liên tục trên \lbrack a;bbrack. Khi đó thể tích của vật thể tròn xoay giới hạn bởi y = f(x),y = g(x) (với 0 < g(x) < f(x)) và hai đường thẳng x = a,x = b khi quay quanh trục Ox là V = \pi\int_{a}^{b}{\left\lbrack f^{2}(x) - g^{2}(x) ightbrack dx}.

  • Câu 15: Thông hiểu
    Tính diện tích hình phẳng D

    Tính diện tích S_{D} của hình phẳng D được giới hạn bởi các đường y = \left| \frac{\ln x}{x} ight|, trục hoành và các đường thẳng x = \frac{1}{e};x = 2?

    Hướng dẫn:

    Diện tích hình phẳng cần tìm là:

    S_{D} = \int_{\frac{1}{e}}^{2}{\left| \frac{\ln x}{x} ight|dx} = \int_{\frac{1}{e}}^{1}{\left| \frac{\ln x}{x} ight|dx} + \int_{1}^{2}{\left| \frac{\ln x}{x} ight|dx}

    = - \int_{\frac{1}{e}}^{1}{\frac{\ln x}{x}dx} + \int_{1}^{2}{\frac{\ln x}{x}dx}

    = - \left. \ \frac{\left( \ln x ight)^{2}}{2} ight|_{\frac{1}{e}}^{1} + \left. \ \frac{\left( \ln x ight)^{2}}{2} ight|_{1}^{2}

    = \frac{1}{2} + \frac{\ln^{2}2}{2} =\frac{1}{2}\left( 1 + \ln^{2}2 ight)

  • Câu 16: Thông hiểu
    Tính thể tích khối tròn xoay

    Tính thể tích khối tròn xoay khi cho hình phẳng giới hạn bởi đồ thị các hàm số y = x^{2} - 2x và y = - x^{2} quay quanh trục Ox.

    Hướng dẫn:

    Xét phương trình hoành độ giao điểm

    x^{2} - 2x = - x^{2} \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 1 \\ \end{matrix} ight.

    Khi đó thể tích khối tròn xoay có được khi quay hình phẳng giới hạn bởi các đồ thị hàm số

    y = x^{2} - 2x;y = - x^{2} quay quanh trục Ox được tính bởi công thức

    V = \pi\int_{0}^{1}\left| \left( x^{2} - 2x ight)^{2} - \left( - x^{2} ight)^{2} ight|dx

    Ta thấy trên \lbrack 0;1brack thì \left( - x^{2} ight)^{2} \leq \left( x^{2} - 2x ight)^{2}, do vậy ta có công thức

    V = \pi\int_{0}^{1}\left\lbrack - x^{4} + \left( x^{4} - 4x^{3} + 4x^{2} ight) ightbrack dx

    = \pi\int_{0}^{1}\left( - 4x^{3} + 4x^{2} ight)dx = \left. \ \pi.\left( - x^{4} + \frac{4}{3}x^{3} ight) ight|_{0}^{1} = \frac{\pi}{3} (đvtt)

  • Câu 17: Nhận biết
    Chọn khẳng đính đúng

    Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành, đường thẳng x = a;x = b như hình vẽ sau:

    Hỏi khẳng định nào dưới đây là khẳng định đúng?

    Hướng dẫn:

    Dựa vào hình biểu diễn hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành, đường thẳng x = a;x = b ta có: S = - \int_{a}^{c}{f(x)dx} + \int_{c}^{b}{f(x)dx}.

  • Câu 18: Thông hiểu
    Tính thể tích vật thể

    Khi cắt một vật thể hình chiếc niêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( - 2 \leq x \leq 2), mặt cắt là tam giác vuông có một góc 45{^\circ} và độ dài một cạnh góc vuông là \sqrt{14 - 3x^{2}} (như hình vẽ). Tính thể tích vật thể hình chiếc niêm trên.

    9

    Hướng dẫn:

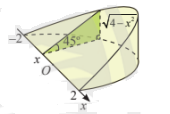
    Diện tích tam giác vuông cân là:

    S(x) = \frac{1}{2}\sqrt{14 - 3x^{2}}.\sqrt{14 - 3x^{2}} = \frac{1}{2}\left( 14 - 3x^{2} \right)

    \Rightarrow Thể tích vật thể là: V = \int_{- 2}^{2}{\frac{1}{2}\left( 14 - 3x^{2} \right)dx = 20}.

  • Câu 19: Thông hiểu
    Tính thể tích khối tròn xoay

    Cho hình phẳng D giới hạn bởi đường cong y = \sqrt{2 + \cos x}, trục hoành và các đường thẳng x = 0, x = \frac{\pi}{2} . Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng bao nhiêu?

    Hướng dẫn:

    Thể tích khối tròn xoay được tạo nên bởi hình phẳng giới hạn bởi các đường y = \sqrt{2 + \cos x}, x = 0, x = \frac{\pi}{2} và trục hoành khi quay quanh Ox là:

    V_{x} = \pi\int_{0}^{\frac{\pi}{2}}{\left( 2 + \cos x ight)dx} = \left. \ \pi\left( 2x + \sin x ight) ight|_{0}^{\frac{\pi}{2}} = \pi(\pi + 1) (đvtt).

  • Câu 20: Thông hiểu
    Tính diện tích S

    Diện tích S của hình phẳng giới hạn bởi đường cong y = - x^{3} + 3x^{2} - 2, trục hoành và hai đường thẳng x = 0;x = 2 là

    Hướng dẫn:

    Phương trình hoành độ giao điểm

    - x^{3} + 3x^{2} - 2 = 0 \Leftrightarrow (1 - x)\left( x^{2} - 2x - 2 ight) = 0

    \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = 1 + \sqrt{3} \\ x = 1 - \sqrt{3} \\ \end{matrix} ight.

    Khi đó:

    S = \int_{0}^{2}{\left| - x^{3} + 3x^{2} - 2 ight|dx}

    = \int_{0}^{1}{\left| - x^{3} + 3x^{2} - 2 ight|dx} + \int_{1}^{2}{\left| - x^{3} + 3x^{2} - 2 ight|dx}

    = \left| \int_{0}^{1}{\left( - x^{3} + 3x^{2} - 2 ight)dx} ight| + \left| \int_{1}^{2}{\left( - x^{3} + 3x^{2} - 2 ight)dx} ight|

    = \left| \left. \ \left( - \frac{x^{4}}{4} + x^{3} - 2x ight) ight|_{0}^{1} ight| + \left| \left. \ \left( - \frac{x^{4}}{4} + x^{3} - 2x ight) ight|_{1}^{2} ight|

    = \frac{5}{2}

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (10%):
    2/3
  • Thông hiểu (75%):
    2/3
  • Vận dụng (15%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Tải file làm trên giấy
1
36 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này