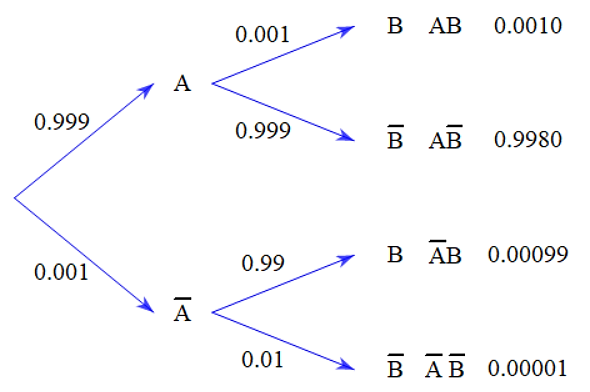
Một xí nghiệp mỗi ngày sản xuất ra sản phẩm trong đó có
sản phẩm lỗi. Lần lượt lấy ra ngẫu nhiên hai sản phẩm không hoàn lại để kiểm tra.
a) Xác suất lấy ra sản phẩm lần thứ nhất bị lỗi là .Đúng||Sai
b) Xác suất lấy ra được cả hai sản phẩm bị lỗi là .Sai||Đúng
c) Xác suất lấy ra sản phẩm lần thứ hai bị lỗi, biết rằng lấy lần thứ nhất sản phẩm không bị lỗi là . Đúng||Sai
d) Xác suất lấy ra sản phẩm lần thứ hai bị lỗi là . Đúng||Sai
Một xí nghiệp mỗi ngày sản xuất ra sản phẩm trong đó có
sản phẩm lỗi. Lần lượt lấy ra ngẫu nhiên hai sản phẩm không hoàn lại để kiểm tra.
a) Xác suất lấy ra sản phẩm lần thứ nhất bị lỗi là .Đúng||Sai
b) Xác suất lấy ra được cả hai sản phẩm bị lỗi là .Sai||Đúng
c) Xác suất lấy ra sản phẩm lần thứ hai bị lỗi, biết rằng lấy lần thứ nhất sản phẩm không bị lỗi là . Đúng||Sai
d) Xác suất lấy ra sản phẩm lần thứ hai bị lỗi là . Đúng||Sai
a) Đ Xét các biến cố:
: Sản phẩm lấy ra lần thứ nhất bị lỗi. Khi đó, ta có:
;
.
: Sản phẩm lấy ra lần thứ hai bị lỗi.
b) S - Khi sản phẩm lấy ra lần thứ nhất bị lỗi thì còn sản phẩm và trong đó có
sản phẩm lỗi nên ta có:
.
c) Đ Khi sản phẩm lấy ra lần thứ nhất không bị lỗi thì còn sản phẩm trong đó có
sản phẩm lỗi nên ta có:
d) Đ - Khi sản phẩm lấy ra lần thứ nhất bị lỗi thì còn sản phẩm và trong đó có
sản phẩm lỗi nên ta có:
, suy ra
.
- Khi sản phẩm lấy ra lần thứ nhất không bị lỗi thì còn sản phẩm trong đó có
sản phẩm lỗi nên ta có:
, suy ra
.
Khi đó, xác suất để sản phẩm lấy ra lần thứ hai bị lỗi là:
.