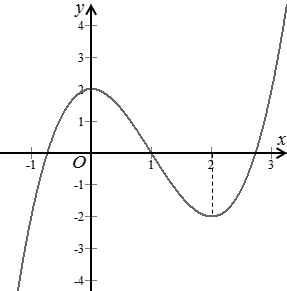
Cho hàm số . Tìm số thực dương
để đường thẳng
cắt đồ thị hàm số tại
điểm phân biệt
,
sao cho tam giác
vuông tại
, trong đó
là gốc tọa độ.
Hoành độ giao điểm của hai đồ thị hàm số là nghiệm của phương trình:
.
Vì hay phương trình
luôn có hai nghiệm phân biệt thỏa mãn:
và
.
Khi đó: ,
.
Ta có tam giác vuông tại
, trong đó
là gốc tọa độ
.
.
Vậy là giá trị cần tìm.