Cho hàm số có đồ thị như sau:
Hỏi số nghiệm của phương trình bằng bao nhiêu?
Ta có:
Lại có đường thẳng nằm phía trên gốc tọa độ; song song với trục Ox và cắt đồ thị hàm số
tại 4 điểm nên phương trình
có hai nghiệm.
Cho hàm số có đồ thị như sau:
Hỏi số nghiệm của phương trình bằng bao nhiêu?
Ta có:
Lại có đường thẳng nằm phía trên gốc tọa độ; song song với trục Ox và cắt đồ thị hàm số
tại 4 điểm nên phương trình
có hai nghiệm.
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?
Dạng đồ thị hình bên là đồ thị hàm số trùng phương có hệ số
.
Do đó, chỉ có đồ thị ở đáp án là thỏa mãn.
Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây?
Từ hình vẽ suy ra đồ thị hàm số bậc 4 trùng phương có hệ số
Đồ thị hàm số đi qua điểm nên hàm số cần tìm là
.
Giả sử hàm số . Có đồ thị là hình bên. Khẳng định nào sau đây là khẳng định đúng?
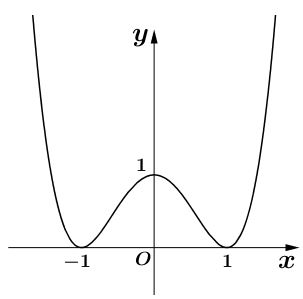
Gọi là giao điểm của đường thẳng
và đường cong
. Khi đó hoành độ
của trung điểm
của đoạn
bằng bao nhiêu?
Pthdgd (*)
Khi đó .
Chú ý: có thể giải (*), tìm được
Cho hàm số liên tục trên
và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình
trên đoạn
là
Ta có .
Dựa vào đồ thị, ta thấy đường thẳng cắt
tại 3 điểm phân biệt nên phương trình đã cho có 3 nghiệm phân biệt.
Tìm giá trị của tham số để đồ thị hàm số
đi qua điểm
?
Đồ thị hàm số đi qua điểm nên ta có:
Đường cong hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
Đồ thị hình vẽ là đồ thị hàm số bậc ba có hệ số nên chỉ có hàm số
thỏa mãn điều kiện trên.
Đường cong trong hình vẽ dưới đây là của hàm số nào?
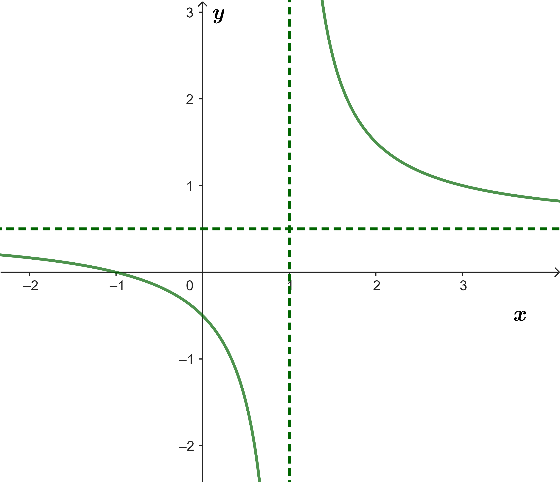
Đường tiệm cận ngang:
Đường tiệm cận đứng:
Cho hàm số . Xét tính đúng sai của nhận định dưới đây:
a) Đạo hàm của hàm số đã cho là . Đúng||Sai
b) Hàm số đã cho đồng biến trên khoảng và nghịch biến trên các khoảng
. Sai||Đúng
c) Bảng biến thiên của hàm số đã cho là:
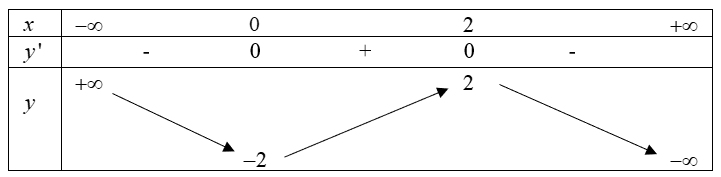
Sai||Đúng
d) Đồ thị hàm số đã cho như ở Hình 4.
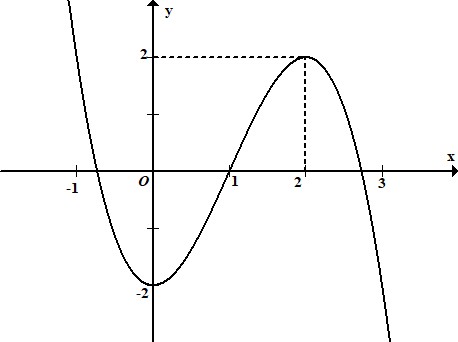
Sai||Đúng
Cho hàm số . Xét tính đúng sai của nhận định dưới đây:
a) Đạo hàm của hàm số đã cho là . Đúng||Sai
b) Hàm số đã cho đồng biến trên khoảng và nghịch biến trên các khoảng
. Sai||Đúng
c) Bảng biến thiên của hàm số đã cho là:

Sai||Đúng
d) Đồ thị hàm số đã cho như ở Hình 4.

Sai||Đúng
|
Câu 2 |
a) |
b) |
c) |
d) |
|
ý |
Đúng |
Sai |
Sai |
Sai |
Ta có: ,
hoặc
.
Bảng biến thiên của hàm số đã cho là:
Hàm số đồng biến trên các khoảng và
, hàm số nghịch biến trên khoảng
.
Đồ thị hàm số đã cho là:
Đồ thị hàm số nào sau đây nhận điểm làm tâm đối xứng?
Đồ thị hàm số có tiệm cận đứng là đường thẳng
và tiệm cận ngang là
suy ra giao điểm của hai đường tiệm cận là
Vậy điểm là tâm đối xứng của đồ thị hàm số
.
Tập tất cả các giá trị của tham số để phương trình
có 4 nghiệm thực phân biệt là
Xét phương trình: .
Đặt .
Phương trình đã cho trở thành .
Để phương trình ban đầu có bốn nghiệm thực phân biệt thì phương trình có hai nghiệm phân biệt dương
hay .
Cho hàm số có đồ thị như hình vẽ bên dưới. Trong các hệ số
,
,
có bao nhiêu số dương?
Tiệm cận đứng:
Tiệm cận ngang:
Đồ thị cắt trục hoành tại nên
hay
Vậy trong các hệ số ,
,
có có hai số dương là
Đồ thị của hàm số dưới đây có dạng như đường cong bên?
Từ đồ thị hàm số đã cho ta nhận dạng được hàm số là hàm số bậc 3 với a > 0.
Suy ra chọn .
Cho hàm số có đồ thị
Tìm số giao điểm của
và trục hoành.
Pthd của và trục hoành là:
có
giao điểm.
Chú ý: Ở bài toán này hoàn toàn có thể giải trực tiếp bằng Casio với phương trình , nhưng chắc chắn thao tác bấm máy sẽ chậm hơn việc tính tay (thậm chí bài này không cần nháp khi mà kết quả đã hiện ra luôn khi ta đọc đề xong). Vì vậy, Casio là điều không cần thiết với câu hỏi này.
Hàm số nào dưới đây có đồ thị như đường cong trong hình bên?
Đường cong trong hình vẽ là đồ thị hàm số với
nên đồ thị đã cho là đồ thị của hàm số
.
Đồ thị được cho dưới đây là đồ thị của hàm số nào?
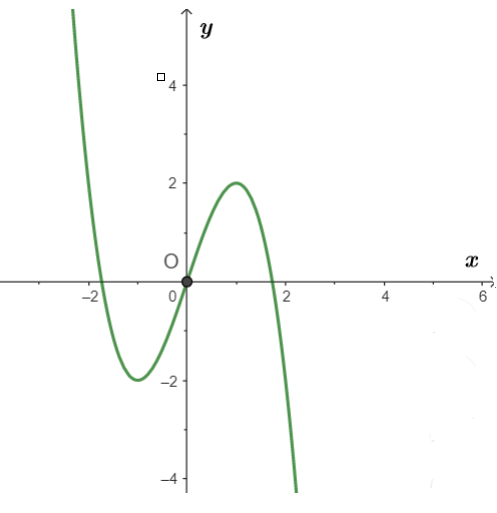
Đồ thị hàm số hình chữ N ngược => Đây là hàm số bậc 3 dạng
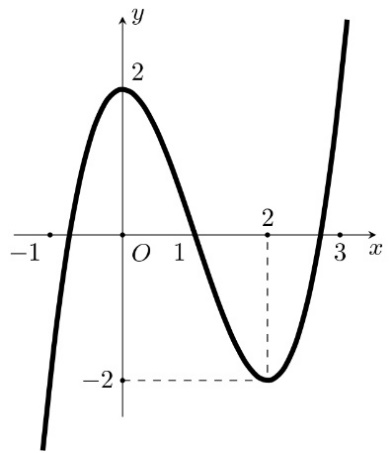
Cho hàm số liên tục trên và có đồ thị như
Xét tính đúng sai của các khẳng định sau:
a) Hàm số không có đạo hàm tại x = −2 và x = 2. Đúng||Sai
b) Hàm số có ba điểm cực trị. Sai||Đúng
c) Giá trị nhỏ nhất của hàm số bằng −2 đạt được tại x = 0. Đúng||Sai
d) Hàm số không có giá trị lớn nhất. Sai||Đúng
Cho hàm số liên tục trên và có đồ thị như
Xét tính đúng sai của các khẳng định sau:
a) Hàm số không có đạo hàm tại x = −2 và x = 2. Đúng||Sai
b) Hàm số có ba điểm cực trị. Sai||Đúng
c) Giá trị nhỏ nhất của hàm số bằng −2 đạt được tại x = 0. Đúng||Sai
d) Hàm số không có giá trị lớn nhất. Sai||Đúng
a) Đúng: Hàm số không có đạo hàm tại x = −2 và x = 2.
b) Sai: Hàm số chỉ có một điểm cực trị là x = 0.
c) Đúng: Giá trị nhỏ nhất của hàm số bằng −2 đạt được tại x = 0.
d) Sai: Ta thấy , và có xảy ra dấu bằng nên hàm số
có giá trị lớn nhất.
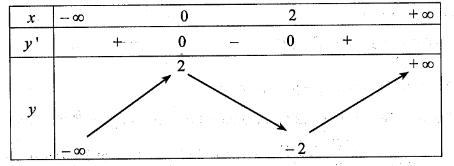
Cho hàm số có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số để phương trình
có ba nghiệm phân biệt?
Ta có:
Để phương trình có ba nghiệm phân biệt thì
Vậy có 1 giá trị nguyên của m thỏa mãn yêu cầu.
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án dưới đây. Hỏi hàm số đó là hàm số nào?
Từ đồ thị : và đây là đồ thị hàm bậc ba nên ta chọn phương án
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

