Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Trắc nghiệm Toán 12 Kết nối tri thức
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập trắc nghiệm Toán 12 KNTT Bài 1 (Mức độ Khó)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Thông hiểu
    Chọn đáp án đúng

    Cho hàm số f(x) có đạo hàm . Gọi P là giá trị cực đại của hàm số đã cho. Chọn khẳng định đúng.

    Hướng dẫn:

     Ta có: f'\left( x ight) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = \pm 3} \\ {x = 0} \end{array}} ight.

    Ta có bảng biến thiên như sau:

    Chọn đáp án đúng

    Dựa vào bảng biến thiên ta có giá trị cực đại của hàm số là P = f(-3)

  • Câu 2: Vận dụng cao
    Ghi đáp án vào ô trống

    Cho hàm số y = f(x) liên tục trên tập số thực và có đạo hàm f'\left( x ight) = {x^2}\left( {x - 2} ight)\left( {{x^2} - 6x + m} ight) với mọi x \in \mathbb{R}. Có bao nhiêu số nguyên m thuộc đoạn [-2019; 2019] để hàm số g\left( x ight) = f\left( {1 - x} ight) nghịch biến trên khoảng \left( { - \infty ; - 1} ight)?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) liên tục trên tập số thực và có đạo hàm f'\left( x ight) = {x^2}\left( {x - 2} ight)\left( {{x^2} - 6x + m} ight) với mọi x \in \mathbb{R}. Có bao nhiêu số nguyên m thuộc đoạn [-2019; 2019] để hàm số g\left( x ight) = f\left( {1 - x} ight) nghịch biến trên khoảng \left( { - \infty ; - 1} ight)?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 3: Vận dụng
    Ghi đáp án vào ô trống

    Cho hàm số y = f(x) = \left| x^{3} -3x^{2} + m ight| biết m \in\lbrack - 4;4brack. Có thể có bao nhiêu giá trị nguyên của tham số m để hàm số đã cho có đúng ba điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) = \left| x^{3} -3x^{2} + m ight| biết m \in\lbrack - 4;4brack. Có thể có bao nhiêu giá trị nguyên của tham số m để hàm số đã cho có đúng ba điểm cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 4: Thông hiểu
    Chọn đáp án đúng

    Giá trị cực tiểu y_{CT} của hàm số y = x^{3} - 3x^{2} + 4 là:

    Hướng dẫn:

    Ta có y' = 3x^{2} - 6x,\ \ y'' = 6x - 6

    \begin{matrix} y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 2 \\ \end{matrix} ight.\ \\ y''(0) = - 6,y''(2) = 6 \\ \end{matrix}

    Do đó hàm số đạt cực tiểu tại x = 2 \Rightarrow y_{CT} = y(2) = 0.

  • Câu 5: Thông hiểu
    Xác định hàm số đồng biến trên tập số thực

    Hàm số nào sau đây đồng biến trên \mathbb{R}?

    Hướng dẫn:

    Ta có hàm số y = \left( \frac{5}{4} ight)^{x} có cơ số a = \frac{5}{4} > 1 nên đồng biến trên \mathbb{R}.

    Ngoài ra các hàm số y = \frac{x + 4}{x + 3}; y = x^{4} - 2x^{2} + 1; y = \tan x không thể đồng biến hoặc nghịch biến trên \mathbb{R}.

  • Câu 6: Thông hiểu
    Chọn kết luận đúng

    Cho hàm số y = \frac{x^{3}}{3} - x^{2} + x + 2019

    Hướng dẫn:

    Ta có y' = x^{2} - 2x + 1 = (x - 1)^{2} \geq 0,\forall x và y' = 0 \Leftrightarrow x = 1 (tại hữu hạn điểm)

    Do đó hàm số đã cho đồng biến trên \mathbb{R}

  • Câu 7: Thông hiểu
    Ghi đáp án vào ô trống

    Xác định tổng S tất cả các giá trị nguyên của tham số m để hàm số y = \frac{mx + 4m - 3}{x + m} nghịch biến trên từng khoảng xác định?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Xác định tổng S tất cả các giá trị nguyên của tham số m để hàm số y = \frac{mx + 4m - 3}{x + m} nghịch biến trên từng khoảng xác định?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 8: Vận dụng
    Ghi đáp án vào ô trống

    Xác định các giá trị của tham số m để hàm số y= - x^{4} + 2\left( m^{2} + 3 ight)x^{2} + 2 có ba điểm cực trị sao cho giá trị cực đại của hàm số đạt giá trị nhỏ nhất?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Xác định các giá trị của tham số m để hàm số y= - x^{4} + 2\left( m^{2} + 3 ight)x^{2} + 2 có ba điểm cực trị sao cho giá trị cực đại của hàm số đạt giá trị nhỏ nhất?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 9: Vận dụng
    Tìm các giá trị nguyên tham số m

    Hỏi có bao nhiêu số nguyên m để hàm số y = \left( m^{2} - 1 \right)x^{3} + (m - 1)x^{2} - x + 4 nghịch biến trên khoảng ( - \infty; + \infty).

    Hướng dẫn:

    TH1: m = 1. Ta có: y = - x + 4 là phương trình của một đường thẳng có hệ số góc âm nên hàm số luôn nghịch biến trên \mathbb{R}.

    Do đó nhận m = 1.

    TH2: m = - 1. Ta có: y = - 2x^{2} - x + 4 là phương trình của một đường Parabol nên hàm số không thể nghịch biến trên \mathbb{R}.

    Do đó loại m = - 1.

    TH3: m eq \pm 1. Khi đó hàm số nghịch biến trên khoảng ( - \infty; + \infty) \Leftrightarrow y' \leq 0\ \ \forall x\mathbb{\in R}, dấu “=” chỉ xảy ra ở hữu hạn điểm trên \mathbb{R}.

    \Leftrightarrow 3\left( m^{2} - 1 ight)x^{2} + 2(m - 1)x - 1 \leq 0, \forall x\mathbb{\in R\ \ }

    \Leftrightarrow \left\{ \begin{matrix} a < 0 \\ \Delta' \leq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m^{2} - 1 < 0 \\ (m - 1)^{2} + 3\left( m^{2} - 1 ight) \leq 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} m^{2} - 1 < 0 \\ (m - 1)(4m + 2) \leq 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} - 1 < m < 1 \\ - \frac{1}{2} \leq m \leq 1 \\ \end{matrix} ight.\ \Leftrightarrow - \frac{1}{2} \leq m < 1

    Vì m\mathbb{\in Z} nên m = 0.

    Vậy có 2 giá trị m nguyên cần tìm là m = 0 hoặc m = 1.

  • Câu 10: Vận dụng
    Chọn đáp án đúng

    Có bao nhiêu giá trị nguyên của m để đồ thị hàm số y = -x^{3} +3mx^{2} -3m-1 có điểm cực đại và điểm cực tiểu đối xứng với nhau qua đường thẳng d: x + 8y - 74.

  • Câu 11: Vận dụng
    Tính giá trị biểu thức

    Tổng bình phương của tất cả các giá trị nguyên của tham số m để hàm số y = \left( 3m^{2} - 12 \right)x^{3} + 3(m - 2)x^{2} - x + 2 nghịch biến trên \mathbb{R} là:

    Hướng dẫn:

    Tập xác định: D = \mathbb{R}.

    Ta có: y' = 9\left( m^{2} - 4 ight)x^{2} + 6(m - 2)x - 1.

    Hàm số nghịch biến trên \mathbb{R \Leftrightarrow}y' \leq 0\forall x\mathbb{\in R}( dấu "=" xảy ra tại hữu hạn x\mathbb{\in R})

    TH1: m^{2} - 4 = 0 \Leftrightarrow m = \pm 2.

    + Với m = 2 ta có y' = - 1 \leq 0 \forall x\mathbb{\in R} nên m = 2 thỏa mãn.

    + Với m = - 2 ta có y^{'} = - 24x - 1 \leq 0 \Leftrightarrow x \geq - \frac{1}{24}(không thỏa với mọi x\mathbb{\in R}) nên loại m = - 2.

    TH2: m^{2} - 4 eq 0 \Leftrightarrow m eq \pm 2. Ta có

    y' \leq 0,\forall x\mathbb{\in R} \Leftrightarrow \left\{ \begin{matrix} a = 9\left( m^{2} - 4 ight) < 0 \\ \Delta^{'} = 9(m - 2)^{2} + 9\left( m^{2} - 4 ight) \leq 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} - 2 < m < 2 \\ 0 \leq m \leq 2 \\ \end{matrix} ight.

    \Leftrightarrow 0 \leq m < 2\overset{m\mathbb{\in Z}}{ightarrow}m \in \left\{ 0;1 ight\}

    Vậy m \in \left\{ \ 0\ ;\ 1;2 ight\} \Rightarrow 0^{2} + 1^{2} + 2^{2} = 5.

  • Câu 12: Vận dụng
    Tính giá trị của biểu thức

    Cho hàm số y = 2x^{3} - 3(2a + 1)x^{2} + 6a(a + 1)x + 2 với a là tham số thực. Gọi x_{1},\ x_{2} lần lượt là hoành độ các điểm cực trị của đồ thị hàm số. Tính P = \left| x_{2} - x_{1} \right|.

    Hướng dẫn:

    Ta có y' = 6x^{2} - 6(2a + 1)x + 6a(a + 1)

    y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = a = x_{1} \\ x = a + 1 = x_{2} \\ \end{matrix} ight.

    Vậy P = \left| x_{2} - x_{1} ight| = \left| (a + 1) - a ight| = 1.

    Nhận xét. Nếu phương trình y' = 0 không ra nghiệm đẹp như trên thì ta dùng công thức tổng quát P = \left| x_{2} - x_{1} ight| = \left| \frac{\sqrt{\Delta}}{a} ight|.

  • Câu 13: Thông hiểu
    Xác định tập hợp tham số m thỏa mãn yêu cầu

    Tập hợp tất cả các giá trị của tham số m để hàm số y = x^{4} - 5(m - 3)x^{2} + 3m^{2} - 4 đạt cực tiểu tại x = 0 là:

    Hướng dẫn:

    Ta có: y' = 4x^{3} - 10(m - 3)x

    \Rightarrow y' = 0 \Leftrightarrow\left\lbrack \begin{matrix}x = 0 \\x^{2} = \dfrac{10(m - 3)}{4} \\\end{matrix} ight.

    Trường hợp 1: m - 3 > 0 \Leftrightarrow m > 3. Khi đó ta có bảng xét dấu như sau:

    Dựa vào bảng biến thiên ta thấy x = 0 là điểm cực đại nên trường hợp này không thỏa mãn.

    Trường hợp 2: m - 3 \leq 0 \Leftrightarrow m \leq 3 ta có bảng xét dấu như sau:

    Dựa vào bảng biến thiên ta thấy x = 0 là điểm cực tiểu. Vậy m \leq 3 thỏa mãn yêu cầu bài toán.

  • Câu 14: Vận dụng
    Tìm điều kiện của m thỏa mãn yêu cầu

    Có bao nhiêu giá trị thực của tham số m để hàm số y = \frac{1}{3}x^{3} - \frac{1}{2}(3m + 2)x^{2} + \left( 2m^{2} + 3m + 1 ight)x - 2 có điểm cực đại x_{CÐ} và điểm cực tiểu x_{CT} thỏa mãn biểu thức 3{x_{CÐ}}^{2} - 4x_{CT} = 0?

    Hướng dẫn:

    Ta có: y' = x^{2} - (3m + 2)x + \left( 2m^{2} + 3m + 1 ight) có \Delta = m^{2} \geq 0;\forall m\mathbb{\in R} nên y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 2m + 1 \\ x = m + 1 \\ \end{matrix} ight..

    Hàm số có cực đại và cực tiểu khi và chỉ khi m eq 0.

    Trường hợp 1: \left\{ \begin{matrix} x_{CÐ} = 2m + 1 \\ x_{CT} = m + 1 \\ \end{matrix} ight.

    Do a = \frac{1}{3} > 0 \Rightarrow x_{CÐ} < x_{CT} \Leftrightarrow 2m + 1 < m + 1 \Leftrightarrow m < 0

    Lại có 3{x_{CÐ}}^{2} - 4x_{CT} = 0 \Leftrightarrow 3(2m + 1)^{2} - 4(m + 1) = 0

    \Leftrightarrow 12m^{2} + 8m - 1 = 0 \Leftrightarrow m = \frac{- 2 \pm \sqrt{7}}{6}

    Với điều kiện m < 0 \Rightarrow m = \frac{- 2 - \sqrt{7}}{6} thỏa mãn.

    Trường hợp 2: \left\{ \begin{matrix} x_{CT} = 2m + 1 \\ x_{CÐ} = m + 1 \\ \end{matrix} ight.

    Do a = \frac{1}{3} > 0 \Rightarrow x_{CÐ} < x_{CT} \Leftrightarrow m + 1 < 2m + 1 \Leftrightarrow m > 0

    Lại có 3{x_{CÐ}}^{2} - 4x_{CT} = 0 \Leftrightarrow 3(m + 1)^{2} - 4(2m + 1) = 0

    \Leftrightarrow 3m^{2} - 2m - 1 = 0\Leftrightarrow \left\lbrack \begin{matrix}m = 1 \\m = - \dfrac{1}{3} \\\end{matrix} ight.

    Với điều kiện m > 0 \Rightarrow m = 1 thỏa mãn.

    Vậy có 2 giá trị thực của tham số m thỏa mãn.

  • Câu 15: Vận dụng
    Tính tổng các phần tử của tập S

    Cho hàm số y = \frac{1}{3}x^{3} - mx^{2} + (3 - 2m)x với m là tham số. Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số nghịch biến trên một khoảng có độ dài bằng 2\sqrt{5}. Tính tổng các phần tử của tập hợp S?

    Hướng dẫn:

    Ta có: y' = x^{2} - 2mx + 3 - 2m \Rightarrow \Delta' = m^{2} + 2m - 3

    Dễ thấy nếu \Delta' \leq 0 suy ra hàm số đồng biến trên \mathbb{R} nên trường hợp này không thỏa mãn

    Theo yêu cầu bài toán

    \Leftrightarrow \left\{ \begin{matrix} \Delta' > 0 \\ \left| x_{1} - x_{2} ight| = 2\sqrt{5} \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m^{2} + 2m - 3 > 0 \\ \left( x_{1} + x_{2} ight)^{2} - 4x_{1}x_{2} = 20 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} m \in ( - \infty; - 3) \cup (1; + \infty) \\ 4m^{2} - 4(3 - 2m) = 20 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m \in ( - \infty; - 3) \cup (1; + \infty) \\ \left\lbrack \begin{matrix} m = - 4 \\ m = 2 \\ \end{matrix} ight.\ \\ \end{matrix} ight.

    \Leftrightarrow \left\lbrack \begin{matrix} m = - 4 \\ m = 2 \\ \end{matrix} ight.\ \Rightarrow S = \left\{ - 4;2 ight\}

    Vậy tổng tất cả các phần tử của tập S bằng -2.

  • Câu 16: Vận dụng
    Số điểm cực trị của hàm số

    Cho hàm số y = f(x) có đạo hàm liên tục trên \mathbb{R}. Đồ thị hàm số y f’(x) như hình vẽ bên:

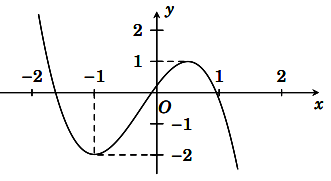
    Số điểm cực trị của hàm số

    Số điểm cực trị của hàm số y = f(x) + 2x là:

    Hướng dẫn:

    Xét hàm số g(x) = f(x) + 2x. Từ đồ thị hàm số f’(x) ta thấy:

    g'\left( x ight) = 0 \Leftrightarrow f'\left( x ight) = - 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = - 1} \\ {x = \alpha } \end{array}} ight.;\left( {\alpha > 0} ight)

    g'\left( x ight) = 0 \Leftrightarrow f'\left( x ight) = - 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = - 1} \\ {x = \alpha } \end{array}} ight.;\left( {\alpha > 0} ight)

    g'\left( x ight) < 0 \Leftrightarrow f'\left( x ight) < - 2 \Leftrightarrow x > \alpha

    Từ đó suy ra hàm số y = f(x) + 2x liên tục và có đạo hàm chỉ đổi dấu khi qua giá trị x = \alpha

    Từ đó ta có bảng xét dấu như sau:

    Số điểm cực trị của hàm số

    Vậy hàm số đã cho có đúng một cực trị

  • Câu 17: Thông hiểu
    Ghi đáp án vào ô trống

    Cho hàm số y = f(x) có đạo hàm f'(x) = (x - 2)^{2019}\left( x^{2} - x -2 ight)^{2020}(x + 3)^{3}. Hỏi hàm số y = f\left( |x| ight) có bao nhiêu cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số y = f(x) có đạo hàm f'(x) = (x - 2)^{2019}\left( x^{2} - x -2 ight)^{2020}(x + 3)^{3}. Hỏi hàm số y = f\left( |x| ight) có bao nhiêu cực trị?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 18: Thông hiểu
    Xác định m để hàm số đồng biến trên tập xác định

    Tìm tất cả các giá trị thực của tham số m để hàm số y = \frac{x - m}{x + 1} đồng biến trên từng khoảng xác định?

    Hướng dẫn:

    Tập xác định D\mathbb{= R}\backslash\left\{ - 1 ight\}

    Ta có: y' = \frac{m + 1}{(x + 1)^{2}};\forall x eq - 1

    Hàm số đã cho đồng biến trên từng khoảng xác định khi và chỉ khi y' > 0

    \Leftrightarrow \frac{m + 1}{(x + 1)^{2}} > 0 \Leftrightarrow m + 1 > 0 \Leftrightarrow m > - 1

    Vậy đáp án cần tìm là m > - 1.

  • Câu 19: Vận dụng cao
    Tìm khẳng định sai

    Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau:

    Xét hàm số g\left( x ight) = f\left( {\frac{{x - 1}}{2}} ight) - \frac{{{x^3}}}{3} + \frac{{3{x^2}}}{2} - 2x + 3. Khẳng định nào sau đây sai?

    Hướng dẫn:

    Ta có:

    g'\left( x ight) = \frac{1}{2}f'\left( {\frac{{x - 1}}{2}} ight) - \left( {{x^2} - 3x + 2} ight)

    f'\left( {\frac{{x - 1}}{2}} ight) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {\dfrac{{x - 1}}{2} = \dfrac{{ - 5}}{2}} \\ {\dfrac{{x - 1}}{2} = - 1} \\ {\dfrac{{x - 1}}{2} = \frac{1}{2}} \\ {\dfrac{{x - 1}}{2} = 3} \end{array}} ight. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = - 4} \\ {x = - 1} \\ {x = 2} \\ {x = 7} \end{array}} ight.

    f'\left( {\frac{{x - 1}}{2}} ight) > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {\dfrac{{x - 1}}{2} < - \dfrac{5}{2}} \\ {\dfrac{1}{2} < \dfrac{{x - 1}}{2} < 3} \end{array}} ight. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x < - 4} \\ {2 < x < 7} \end{array}} ight.

    Ta có bảng xét dấu cho các biểu thức

    Tìm khẳng định sai

    Từ bảng xét dấu ta thấy

    x \in \left( {0;1} ight) \subset \left( {0;2} ight) \Rightarrow g'\left( x ight) < 0

    Khi đó hàm số nghịch biến

    => Đáp án B sai

  • Câu 20: Vận dụng
    Tính tổng P

    Gọi P là tập hợp các giá trị nguyên của tham số m để hàm số y = {x^3} - 3\left( {m - 2} ight){x^2} + 12x + 1 đồng biến trên tập xác định của nó. Tổng các phần tử của tập hợp P là:

    Hướng dẫn:

    Ta có: y' = 3{x^2} - 6\left( {m - 2} ight)x + 12

    Hàm số đồng biến trên \mathbb{R} khi và chỉ khi

    \begin{matrix} y' \geqslant 0,\forall x \in \mathbb{R} \hfill \\ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a = 3 > 0} \\ {\left( {{\Delta _{y'}}} ight)' = 9{{\left( {m - 2} ight)}^2} - 36 \leqslant 0} \end{array}} ight. \Leftrightarrow 0 \leqslant m \leqslant 4 \hfill \\ \end{matrix}

    Kết hợp với điều kiện m \in \mathbb{Z}

    => m \in \left\{ {0;1;2;3;4} ight\}

    => Tổng P bằng 10

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (40%):
    2/3
  • Thông hiểu (50%):
    2/3
  • Vận dụng (10%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
1
25 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Trắc nghiệm Toán 12 Kết nối tri thức
Xem thêm