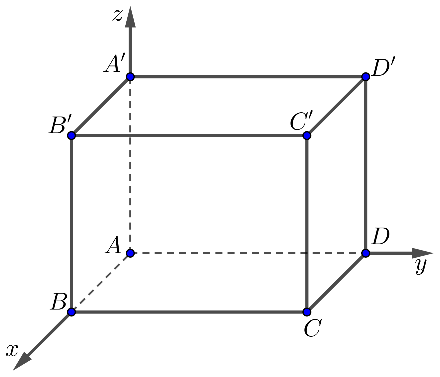
Trong không gian , cho hình lập phương
có cạnh bằng 4, đỉnh
trùng với gốc
, các điểm
lần lượt nằm trên các tia
.
a. Tọa độ của điểm là:
Sai||Đúng
b. Tọa độ của vec tơ là:
Sai||Đúng
c. Tọa độ của vec tơ là:
Đúng||Sai
d. Tọa độ của vec tơ là:
Đúng||Sai
Trong không gian , cho hình lập phương
có cạnh bằng 4, đỉnh
trùng với gốc
, các điểm
lần lượt nằm trên các tia
.
a. Tọa độ của điểm là:
Sai||Đúng
b. Tọa độ của vec tơ là:
Sai||Đúng
c. Tọa độ của vec tơ là:
Đúng||Sai
d. Tọa độ của vec tơ là:
Đúng||Sai
Hình vẽ minh họa
(a) Tọa độ của điểm là:
Do cùng hướng với
và
nên
hay
.
Suy ra: .
» Chọn SAI.
(b) Tọa độ của vec tơ là:
Do cùng hướng với
và
nên
hay
.
Theo quy tắc hình bình hành, ta có: .
Suy ra: .
» Chọn SAI.
(c) Tọa độ của vec tơ là:
Do cùng hướng với
và
nên
hay
.
Suy ra: .
» Chọn ĐÚNG.
(d) Tọa độ của vec tơ là:
.
Theo quy tắc hình hộp, ta có: .
Suy ra:
» Chọn ĐÚNG.