VnDoc.com Lớp 12

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Trắc nghiệm Toán 12 Chân trời sáng tạo Bài 1 (Mức Dễ)

Nhận biết Thông hiểu Vận dụng Vận dụng cao

Bài kiểm tra này bao gồm 15 câu
Điểm số bài kiểm tra: 15 điểm
Xem lại kỹ lý thuyết trước khi làm bài
Chuẩn bị giấy và bút để nháp trước khi bắt đầu

Bắt đầu!!

00:00:00

Câu 1: Nhận biết
Tìm khoảng biến thiên của mẫu số liệu ghép nhóm
Đo chiều cao (tính bằng $cm$ ) của $500$ học sinh trong một trường THPT ta thu được kết quả như sau:

Chiều cao
$\lbrack 150;\ 154)$ $\lbrack 154;\ 158)$ $\lbrack 158;\ 162)$ $\lbrack 162;\ 166)$ $\lbrack 166;\ 170)$

Số học sinh

25

50

200

175

50

Khoảng biến thiên của mẫu số liệu trên là
- A.
  $6$ .
- B.
  $20$ .
- C.
  $4$ .
- D.
  $16$ .
Hướng dẫn:
Khoảng biến thiên của mẫu số liệu trên là $R = 170 - 150 = 20$
Câu 2: Nhận biết
Tìm khoảng biến thiên
Thống kê thời gian sử dụng mạng xã hội trong ngày của các bạn học sinh tổ 1 và tổ 2 lớp 12A thu được bảng sau:

Tìm khoảng biến thiên $R_{1},\ R_{2}$ cho thời gian sử dụng mạng xã hội của tổ 1 và tổ 2.
- A.
  $R_{1} = 10;\ \ R_{2} = 30$ .
- B.
  $R_{1} = 30;\ \ R_{2} = 30$ .
- C.
  $R_{1} = 60;\ \ R_{2} = 90$ .
- D.
  $R_{1} = 90;\ \ R_{2} = 60$ .
Hướng dẫn:
Khoảng biến thiên của mẫu số liệu ghép nhóm của tổ 1: $R_{1} = 90$

Khoảng biến thiên của mẫu số liệu ghép nhóm của tổ 2: $R_{2} = 60$
Câu 3: Nhận biết

Xác định tính đúng sai của từng phương án

Cho mẫu số liệu ghép nhóm về thời gian (đơn vị: phút) đi từ nhà đến trường của các học sinh trong một lớp 12 của một trường như sau:

Thời gian

[0; 5)

[5; 10)

[10; 15)

[15; 20)

[20; 25)

[25; 30)

Số học sinh

7

12

7

5

3

2

Xét tính đúng sai của các khẳng định sau:

a) Tần số tích lũy của nhóm [10;15) là 26. Đúng||Sai

b) Tần số nhóm [10;15) lớn nhất. Đúng||Sai

c) Khoảng biến thiên là 15. Sai||Đúng

d) Giá trị trung bình của mẫu số liệu bằng 11,25. Đúng||Sai

Đáp án là:

Cho mẫu số liệu ghép nhóm về thời gian (đơn vị: phút) đi từ nhà đến trường của các học sinh trong một lớp 12 của một trường như sau:

Thời gian

[0; 5)

[5; 10)

[10; 15)

[15; 20)

[20; 25)

[25; 30)

Số học sinh

7

12

7

5

3

2

Xét tính đúng sai của các khẳng định sau:

a) Tần số tích lũy của nhóm [10;15) là 26. Đúng||Sai

b) Tần số nhóm [10;15) lớn nhất. Đúng||Sai

c) Khoảng biến thiên là 15. Sai||Đúng

d) Giá trị trung bình của mẫu số liệu bằng 11,25. Đúng||Sai

a) Đúng: Tần số tích lũy của nhóm [10;15) là $7 + 12 + 7 = 26$

b) Đúng: Tần số nhóm [10;15) lớn nhất.

c) Sai: Khoảng biến thiên là $R = 30 – 0 = 30$

d) Đúng: Giá trị trung bình của mẫu số liệu bằng:

$\overline{x} = \frac{2,5.7 + 7,5.12 + 12,5.7 + 17,5.5 + 22,5.3 + 27,5.2}{36} = 11,26$
Câu 4: Nhận biết
Tìm khoảng biến thiên của mẫu số liệu ghépnhóm
Biểu đồ sau biểu diễn tốc độ tăng trưởng GDP của Nhật Bản trong giai đoạn 1990 đến 2005. Hãy tìm khoảng biến thiên của mẫu số liệu đó.
- A.
  0,4
- B.
  5,1
- C.
  5,5
- D.
  4,7.
Hướng dẫn:
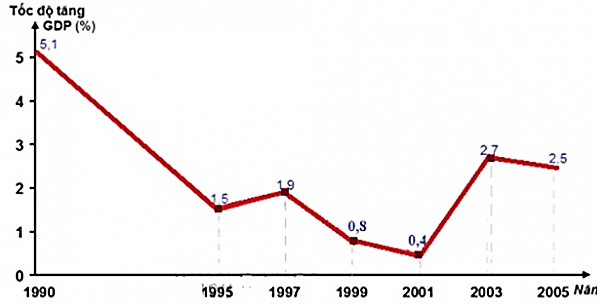
Ta có giá trị lớn nhất của mẫu số liệu là 5,1 và giá trị nhỏ nhất của mẫu số liệu là 0,4

⇒ R = 5,1 – 0,4 = 4,7.
Câu 5: Nhận biết
Chọn đáp án đúng
Khoảng biến thiên của mẫu số liệu ghép nhóm được cho ở bảng sau là bao nhiêu?

Nhóm
$\lbrack 15;22)$ $\lbrack 22;29)$ $\lbrack 29;36)$ $\lbrack 36;43)$ $\lbrack 43;50)$

Tần số
$1$ $6$ $21$ $21$ $11$
- A.
  35
- B.
  34
- C.
  33
- D.
  32
Hướng dẫn:
Khoảng biến thiên của mẫu số liệu ghép nhóm ở bảng trên là:

$R = a_{6} - a_{1} = 50 - 15 = 35$
Câu 6: Nhận biết
Xác định khoảng biến thiên của mẫu số liệu ghép nhóm
Cho bảng số liệu ghép nhóm về chiều cao (đơn vị centimét) của 36 học sinh trong lớp 12A1 như sau:

Xác định khoảng biến thiên của mẫu số liệu ghép nhóm?
- A.
  30
- B.
  25
- C.
  20
- D.
  35
Hướng dẫn:
Ta có khoảng biến thiên của mẫu số liệu ghép nhóm trên là:

$R = a_{k + 1} - a_{1} = 180 - 150 = 30$ .
Câu 7: Nhận biết
Tìm khoảng biến thiên của mẫu số liệu ghép nhóm
Khoảng biến thiên của mẫu số liệu ghép nhóm được cho ở bảng sau là bao nhiêu?

Nhóm
$\lbrack 15;22)$ $\lbrack 22;29)$ $\lbrack 29;36)$ $\lbrack 36;43)$ $\lbrack 43;50)$

Tần số
1 6 21 21 11
- A.
  40
- B.
  45
- C.
  30
- D.
  35
Hướng dẫn:
Khoảng biến thiên của mẫu số liệu ghép nhóm là 50 – 15 = 35
Câu 8: Nhận biết
Tìm nhóm chứa tứ phân vị thứ nhất
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:

Tuổi thọ

[14; 15)

[15; 16)

[16; 17)

[17; 18)

[18; 19)

Số con hổ

1

3

8

6

2

Nhóm chứa tứ phân vị thứ nhất là
- A.
  [14; 15).
- B.
  [15; 16).
- C.
  [17; 18).
- D.
  [16; 17).
Hướng dẫn:
Cỡ mẫu là: 1 + 3 + 8 + 6 + 2 = 20.

Gọi x₁; x₂; …; x₂₀ là tuổi thọ của 20 con hổ được sắp xếp theo thứ tự tăng dần

Tứ phân vị thứ nhất của mẫu số liệu gốc là $\left\lbrack \frac{x_{5} + x_{6}}{2} \right\rbrack \in$ [16; 17) nên nhóm chứa tứ phân vị thứ nhất là [16; 17).
Câu 9: Nhận biết
Tìm khoảng biến thiên của mẫu số liệu
Cho mẫu số liệu ghép nhóm cho bởi bảng sau:

Nhóm

[0; 10)

[10; 20)

[20; 30)

[30; 40)

Tần số

3

7

2

9

Khoảng biến thiên của mẫu số liệu ghép nhóm này là
- A.
  $50$ .
- B.
  $40$ .
- C.
  $60$ .
- D.
  $70$ .
Hướng dẫn:
Khoảng biến thiên của mẫu số liệu ghép nhóm là:

R = 40 – 0 = 40.
Câu 10: Nhận biết
Chọn công thức tính khoảng tứ phân vị
Công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm là
- A.
  $\Delta_{Q} = Q_{3}.Q_{1}$ .
- B.
  $\Delta_{Q} = Q_{3} + Q_{1}$ .
- C.
  $\Delta_{Q} = Q_{1} - Q_{3}$ .
- D.
  $\Delta_{Q} = Q_{3} - Q_{1}$ .
Hướng dẫn:
Công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm là: $\Delta_{Q} = Q_{3} - Q_{1}$

Câu 11: Thông hiểu

Chọn đáp án đúng

Cho mẫu dữ liệu ghép nhóm được ghi trong bảng dưới đây:

Khoảng	Tần số
Nhỏ hơn 10	10
Nhỏ hơn 20	20
Nhỏ hơn 30	30
Nhỏ hơn 40	40
Nhỏ hơn 50	50
Nhỏ hơn 60	30

Tìm khoảng tứ phân vị của mẫu số liệu đã cho?

A.
$\Delta_{Q} = 25,02$
B.
$\Delta_{Q} = 21,25$
C.
$\Delta_{Q} = 23,64$
D.
$\Delta_{Q} = 20,78$

Hướng dẫn:

Ta có:

Nhóm dữ liệu	Tần số	Tần số tích lũy
(0; 10]	10	10
(10; 20]	20	30
(20; 30]	30	60
(30; 40]	50	110
(40; 50]	40	150
(50; 60]	30	180
Tổng	N = 180

Ta có: $\frac{N}{4} = \frac{180}{4} = 45$

=> Nhóm chứa tứ phân vị thứ nhất là: (20; 30]

Khi đó: $\left\{ \begin{matrix} l = 20;\frac{N}{4} = 45 \\ m = 30,f = 30,d = 10 \\ \end{matrix} ight.$

Tứ phân vị thứ nhất là:

$Q_{1} = l + \frac{\frac{N}{4} - m}{f}.d$

$\Rightarrow Q_{1} = 20 + \frac{45 - 30}{30}.10 = 25$

Ta có: $\frac{3N}{4} = \frac{3.180}{4} = 135$

=> Nhóm chứa tứ phân vị thứ ba là: (40; 50]

Khi đó: $\left\{ \begin{matrix} l = 40;\frac{3N}{4} = 30 \\ m = 110,f = 40,d = 10 \\ \end{matrix} ight.$

Tứ phân vị thứ ba là:

$Q_{3} = l + \frac{\frac{3N}{4} - m}{f}.d$

$\Rightarrow Q_{3} = 40 + \frac{135 - 110}{40}.10 = \frac{185}{4}$

$\Rightarrow \Delta_{Q} = Q_{3} - Q_{1} = \frac{185}{4} - 25 = 21,25$

Câu 12: Thông hiểu

Xét tính đúng sai của các khẳng định

Trường THPT A khảo sát chiều cao của học sinh khối 10, kết quả ghi lại chiều cao (tính theo đơn vị cm) của học sinh lớp 10A được cho trong bảng sau:

Xét tính đúng sai của các kết luận sau?

a) Khoảng biến thiên của mẫu số liệu ghép nhóm là $R = 45$ . Sai||Đúng

b) Số phần tử của mẫu là $n = 30$ . Sai||Đúng

c) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là $Q_{1} = \frac{3685}{24}$ . Đúng||Sai

d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là $\Delta_{Q} \approx 8,62$ . Đúng||Sai

Đáp án là:

Trường THPT A khảo sát chiều cao của học sinh khối 10, kết quả ghi lại chiều cao (tính theo đơn vị cm) của học sinh lớp 10A được cho trong bảng sau:

Xét tính đúng sai của các kết luận sau?

a) Khoảng biến thiên của mẫu số liệu ghép nhóm là $R = 45$ . Sai||Đúng

b) Số phần tử của mẫu là $n = 30$ . Sai||Đúng

c) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là $Q_{1} = \frac{3685}{24}$ . Đúng||Sai

d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là $\Delta_{Q} \approx 8,62$ . Đúng||Sai

a) Sai

Ta có $R = 170 - 140 = 30$ .

b) Sai

Ta có $n = 45$ .

c) Đúng

Ta có $n = 45 \Rightarrow \frac{n}{4} = 11,25 \Rightarrow 7 < 11,25 < 13$

=> Nhóm ba là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $11,25$

Nhóm chứa tứ phân vị thứ nhất là nhóm $\lbrack 150;155)$

$\Rightarrow Q_{1} = 150 + \frac{\frac{45}{4} - 7}{6}.5 = \frac{3685}{24}$

d) Đúng

Ta có $n = 45 \Rightarrow \frac{3n}{4} = 33,75 \Rightarrow 29 < 33,75 < 40$

=> Nhóm năm là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $33,75$

Nhóm chứa tứ phân vị thứ ba là nhóm $\lbrack 160;165)$

$\Rightarrow Q_{3} = 160 + \frac{\frac{3.45}{4} - 29}{11}.5 = \frac{7135}{44}$

Khoảng tứ phân vị của mẫu số liệu là $\Delta Q = Q_{3} - Q_{1} = \frac{7135}{44} - \frac{3685}{24} = \frac{2275}{264} \approx 8,62$

Câu 13: Thông hiểu

Tìm tứ phân vị thứ ba của mẫu số liệu

Thực hiện khảo sát chi phí thanh toán cước điện thoại trong 1 tháng của cư dân trong một chung cư thu được kết quả ghi trong bảng sau:

Số tiền (nghìn đồng)	Số người
[0; 50)	5
[50; 100)	12
[100; 150)	23
[150; 200)	17
[200; 250)	3

Tính $Q_{3}$ ?

A.
$162,6$
B.
$164,7$
C.
$160,8$
D.
$158,3$

Hướng dẫn:

Ta có:

Số tiền (nghìn đồng)	Số người	Tần số tích lũy
[0; 50)	5	5
[50; 100)	12	17
[100; 150)	23	40
[150; 200)	17	57
[200; 250)	3	60
	N = 60

Cỡ mẫu là: $N = 60 \Rightarrow \frac{3N}{4} = 45$

=> Nhóm chứa tứ phân vị thứ ba là [150; 200) (vì 45 nằm giữa hai tần số tích lũy 40 va 57)

Khi đó $\left\{ \begin{matrix}l = 150;\dfrac{3N}{4} = 45;m = 40;f = 17 \\c = 200 - 150 = 50 \\\end{matrix} ight.$

$\Rightarrow Q_{3} = l +\dfrac{\dfrac{3N}{4} - m}{f}.c$

$\Rightarrow Q_{3} = 150 + \frac{45 - 40}{17}.50 = \frac{2800}{17}$

Câu 14: Thông hiểu

Xác định tính đúng sai của từng phương án

Cho mẫu số liệu ghép nhóm về chiều cao (đơn vị: cm) của cây trong vườn nghiên cứu như sau:

Chiều cao

[40; 45)

[45; 50)

[50; 55)

[55; 60)

[60; 65)

[65; 70)

Số cây

5

10

7

9

7

4

Xét tính đúng sai của các khẳng định sau:

a) Nhóm [45; 50) có tần số tích luỹ là 15. Đúng||Sai

b) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 30. Đúng||Sai

c) Nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng $\frac{3n}{4}$ là nhóm [55; 60). Sai||Đúng

d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là $Q_{3} > 61$ . Sai||Đúng

Đáp án là:

Cho mẫu số liệu ghép nhóm về chiều cao (đơn vị: cm) của cây trong vườn nghiên cứu như sau:

Chiều cao

[40; 45)

[45; 50)

[50; 55)

[55; 60)

[60; 65)

[65; 70)

Số cây

5

10

7

9

7

4

Xét tính đúng sai của các khẳng định sau:

a) Nhóm [45; 50) có tần số tích luỹ là 15. Đúng||Sai

b) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 30. Đúng||Sai

c) Nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng $\frac{3n}{4}$ là nhóm [55; 60). Sai||Đúng

d) Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là $Q_{3} > 61$ . Sai||Đúng

a) Đúng: Nhóm [45;50) có tần số tích luỹ là $5 + 10 = 15$ .

b) Đúng: Khoảng biến thiên là $70 – 40 = 30$

c) Sai: Nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng $\frac{n}{2} = 31,5$ là nhóm [60; 65).

d) Sai: Nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng $\frac{n}{2} = 31,5$ là nhóm [60; 65).

Đầu mút trái, độ dài và tần số của nhóm [60; 65) lần lượt là $s = 60;h = 5;n_{2} = 7$ .

Tần số tích luỹ của nhóm liền trước là $cf_{4} = 31$ nên tứ phân vị thứ ba là:

$Q_{1} = 60 + \left( \frac{31,5 - 31}{7} ight).5 \approx 60,36$

Câu 15: Thông hiểu

Xác định khoảng tứ phân vị của mẫu số liệu

Cho mẫu số liệu ghép nhóm như sau:

Nhóm	Tần số
[0; 20)	16
[20; 40)	12
[40; 60)	25
[60; 80)	15
[80; 100)	12
[100; 120)	10
Tổng	N = 90

Xác định khoảng tứ phân vị của mẫu số liệu? Kết quả làm tròn đến chữ số thập phân thứ nhất.

A.
$\Delta_{Q} = 43,7$
B.
$\Delta_{Q} = 42,4$
C.
$\Delta_{Q} = 48,5$
D.
$\Delta_{Q} = 46,2$

Hướng dẫn:

Ta có:

Nhóm	Tần số	Tần số tích lũy
[0; 20)	16	16
[20; 40)	12	28
[40; 60)	25	53
[60; 80)	15	68
[80; 100)	12	80
[100; 120)	10	90
Tổng	N = 90

Ta có: $\frac{N}{4} = 22,5$

=> Nhóm chứa tứ phân vị thứ nhất là: [20; 40)

Khi đó ta có: $\left\{ \begin{matrix}l = 20;\dfrac{N}{4} = 22,5 \\m = 16,f = 12,d = 20 \\\end{matrix} ight.$

Tứ phân vị thứ nhất được tính như sau:

$Q_{1} = l + \dfrac{\dfrac{N}{4} -m}{f}.d$

$\Rightarrow Q_{1} = 20 + \frac{22,5 - 16}{12}.20 = \frac{185}{6}$

Ta có: $\frac{3N}{4} = 67,5$

=> Nhóm chứa tứ phân vị thứ ba là: [60; 80)

Khi đó ta có: $\left\{ \begin{matrix} l = 60;\frac{3N}{4} = 67,5 \\ m = 53,f = 15,80 - 60 = 20 \\ \end{matrix} ight.$

Tứ phân vị thứ ba được tính như sau:

$Q_{3} = l + \dfrac{\dfrac{3N}{4} -m}{f}.d$

$\Rightarrow Q_{3} = 60 + \frac{67,5 - 53}{15}.20 = \frac{238}{3}$

$\Rightarrow \Delta_{Q} = Q_{3} - Q_{1} = \frac{238}{3} - \frac{185}{6} = 48,5$

0/15

15 câu:

Kiểm tra Kiểm tra lại Tiếp tục Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:

Nhận biết (67%):

2/3
Thông hiểu (33%):

2/3

Thời gian làm bài: 00:00:00
Số câu làm đúng: 0
Số câu làm sai: 0
Điểm số: 0
Điểm thưởng: 0

Làm lại

Chia sẻ bởi:
Bon

18 Bài viết đã được lưu

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Số điện thoại này đã được xác thực!

Bạn có thể dùng Sđt này đăng nhập tại đây!

Lỗi gửi SMS, liên hệ Admin

Sắp xếp theo

Xóa Đăng nhập để Gửi

Tìm bài trong mục này

Trắc nghiệm Toán 12 Kết nối tri thức
Trắc nghiệm Toán 12 Chân trời sáng tạo
Trắc nghiệm Toán 12 Cánh diều
Trắc nghiệm Toán 12 Sách cũ

Lớp 12

Lớp 12

Bộ đề thi giữa kì 2 Toán 12 Kết nối tri thức - Số 5 (CV 7991)
Đề thi giữa kì 2 Toán 12 Kết nối tri thức - Đề 18 (CV 7991)
Đề thi giữa kì 2 Toán 12 Kết nối tri thức - Đề 17 (CV 7991)
Đề thi giữa kì 2 Toán 12 Kết nối tri thức - Đề 19 (CV 7991)
Đề thi giữa kì 2 Toán 12 Kết nối tri thức - Đề 20 (CV 7991)
Đề thi giữa kì 2 Toán 12 Kết nối tri thức - Đề 16 (CV 7991)

Xem thêm

Chiều cao	$\lbrack 150;\ 154)$	$\lbrack 154;\ 158)$	$\lbrack 158;\ 162)$	$\lbrack 162;\ 166)$	$\lbrack 166;\ 170)$
Số học sinh	25	50	200	175	50

Thời gian	[0; 5)	[5; 10)	[10; 15)	[15; 20)	[20; 25)	[25; 30)
Số học sinh	7	12	7	5	3	2

Nhóm	$\lbrack 15;22)$	$\lbrack 22;29)$	$\lbrack 29;36)$	$\lbrack 36;43)$	$\lbrack 43;50)$
Tần số	$1$	$6$	$21$	$21$	$11$

Tuổi thọ	[14; 15)	[15; 16)	[16; 17)	[17; 18)	[18; 19)
Số con hổ	1	3	8	6	2

Chiều cao	[40; 45)	[45; 50)	[50; 55)	[55; 60)	[60; 65)	[65; 70)
Số cây	5	10	7	9	7	4

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Trắc nghiệm Toán 12 Chân trời sáng tạo Bài 1 (Mức Dễ)

Chúc mừng Bạn đã hoàn thành bài!

Trắc nghiệm Toán 12 Kết nối tri thức

Trắc nghiệm Toán 12 Chân trời sáng tạo

Trắc nghiệm Toán 12 Cánh diều

Trắc nghiệm Toán 12 Sách cũ

Lớp 12

Lớp 12

Bộ đề thi giữa kì 2 Toán 12 Kết nối tri thức - Số 5 (CV 7991)

Đề thi giữa kì 2 Toán 12 Kết nối tri thức - Đề 18 (CV 7991)

Đề thi giữa kì 2 Toán 12 Kết nối tri thức - Đề 17 (CV 7991)

Đề thi giữa kì 2 Toán 12 Kết nối tri thức - Đề 19 (CV 7991)

Đề thi giữa kì 2 Toán 12 Kết nối tri thức - Đề 20 (CV 7991)

Đề thi giữa kì 2 Toán 12 Kết nối tri thức - Đề 16 (CV 7991)