Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Trắc nghiệm Toán 12 Kết nối tri thức
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Khó)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Thông hiểu
    Xét tính đúng sai của các phương án

    Ông Bình hằng ngày đi làm bằng xe máy hoặc xe buýt. Nếu hôm nay ông đi làm bằng xe buýt thì xác suất để hôm sau ông đi làm bằng xe máy là 0,4. Nếu hôm nay ông đi làm bằng xe máy thì xác suất để hôm sau ông đi làm bằng xe buýt là 0,7. Xét một tuần mà thứ Hai ông Bình đi làm bằng xe buýt.

    Gọi A là biến cố: “Thứ Ba, ông Bình đi làm bằng xe máy” và B là biến cố: “Thứ Tư, ông Bình đi làm bằng xe máy”.

    a) Xác suất để thứ Ba, ông Bình đi làm bằng xe buýt là \frac{7}{10}. Sai||Đúng

    b) Xác suất để thứ Tư, ông Bình đi làm bằng xe máy nếu thứ Ba, ông An đi làm bằng xe máy là \frac{3}{10}. Đúng||Sai

    c) Xác suất để thứ Tư, ông Bình đi làm bằng xe máy nếu thứ Ba ông Bình đi làm bằng xe buýt là \frac{4}{10}. Đúng||Sai

    d) Xác suất để thứ Tư trong tuần đó, ông Bình đi làm bằng xe máy nếu thứ Hai ông Bình đi làm bằng xe buýt là \frac{9}{25}. Đúng||Sai

    Đáp án là:

    Ông Bình hằng ngày đi làm bằng xe máy hoặc xe buýt. Nếu hôm nay ông đi làm bằng xe buýt thì xác suất để hôm sau ông đi làm bằng xe máy là 0,4. Nếu hôm nay ông đi làm bằng xe máy thì xác suất để hôm sau ông đi làm bằng xe buýt là 0,7. Xét một tuần mà thứ Hai ông Bình đi làm bằng xe buýt.

    Gọi A là biến cố: “Thứ Ba, ông Bình đi làm bằng xe máy” và B là biến cố: “Thứ Tư, ông Bình đi làm bằng xe máy”.

    a) Xác suất để thứ Ba, ông Bình đi làm bằng xe buýt là \frac{7}{10}. Sai||Đúng

    b) Xác suất để thứ Tư, ông Bình đi làm bằng xe máy nếu thứ Ba, ông An đi làm bằng xe máy là \frac{3}{10}. Đúng||Sai

    c) Xác suất để thứ Tư, ông Bình đi làm bằng xe máy nếu thứ Ba ông Bình đi làm bằng xe buýt là \frac{4}{10}. Đúng||Sai

    d) Xác suất để thứ Tư trong tuần đó, ông Bình đi làm bằng xe máy nếu thứ Hai ông Bình đi làm bằng xe buýt là \frac{9}{25}. Đúng||Sai

    Từ giả thiết của bài toán ta có sơ đồ hình cây như sau:

    a) Dựa vào sơ đồ cây ta có xác suất để thứ Ba, ông Bình đi làm bằng xe buýt là 0,6 (nhánh O\overline{A}).

    b) Dựa vào sơ đồ cây ta có xác suất để thứ Tư, ông Bình đi làm bằng xe máy nếu thứ Ba, ông Bình đi làm bằng xe máy là 0,3 = \frac{3}{10} (nhánh \overline{A}B).

    c) Dựa vào sơ đồ cây ta có xác suất để thứ Tư, ông Bình đi làm bằng xe máy nếu thứ Ba ông Bình đi làm bằng xe buýt 0,4 = \frac{4}{10} (nhánh AB)

    d) Xác suất để thứ Tư trong tuần đó, ông Bình đi làm bằng xe máy nếu thứ Hai ông Bình đi làm bằng xe buýt là:

    P(B) = 0,4.0,3 + 0,6.0,4 = 0,36(nhánh OAB và nhánh O\overline{A}B).

  • Câu 2: Vận dụng
    Tính xác suất để hai đứa trẻ là con gái

    Một gia đình có 2 đứa trẻ. Biết rằng có ít nhất 1 đứa trẻ là con gái. Hỏi xác suất 2 đứa trẻ đều là con gái là bao nhiêu? Cho biết xác suất để một đứa trẻ là trai hoặc gái là bằng nhau.

    Hướng dẫn:

    Giới tính cả 2 đứa trẻ là ngẫu nhiên và không liên quan đến nhau.

    Do gia đình có 2 đứa trẻ nên sẽ có thể xảy ra 4 khả năng:

    (trai, trai), (gái, gái), (gái, trai), (trai, gái).

    Gọi A là biến cố “Cả hai đứa trẻ đều là con gái”

    Gọi B là biến cố “Có ít nhất một đứa trẻ là con gái”

    Ta có P(A) = \frac{1}{4};P(B) = \frac{3}{4}

    Do nếu xảy ra A thì đương nhiên sẽ xảy ra B nên ta có:

    P(A \cap B) = P(A) = \frac{1}{4}

    Suy ra, xác suất để cả hai đứa trẻ đều là con gái khi biết ít nhất có một đứa trẻ là gái là

    P\left( A|B \right) = \frac{P(A \cap B)}{P(B)} = \frac{\frac{1}{4}}{\frac{3}{4}} = \frac{1}{3}

  • Câu 3: Thông hiểu
    Chọn phương án thích hợp

    Một nhóm học sinh có 30 học sinh, trong đó có 16 em học khá môn Toán, 25 em học khá môn Hóa học, 12 em học khá cả hai môn Toán và Hóa học. Chọn ngẫu nhiên một học sinh trong số đó. Tính xác suất để học sinh đó học khá môn Toán biết rằng học sinh đó học khá môn Hóa học.

    Hướng dẫn:

    Gọi A: “Học sinh đó học khá môn Toán”,

    Và B: “Học sinh đó học khá môn Hóa học”.

    Từ bài ra ta có P(A) = \frac{16}{30}, P(B) = \frac{25}{30}; P(AB) = \frac{12}{30}.

    P\left( A|B \right) = \frac{P(AB)}{P(B)} = \frac{12}{25} = 0,48.

  • Câu 4: Vận dụng
    Tính xác suất theo yêu cầu

    Tung một con xúc sắc hai lần độc lập nhau. Biết rằng lần tung thứ nhất được số chấm chẵn. Tính xác suất tổng số chấm hai lần tung bằng 4?

    Hướng dẫn:

    Gọi Ti: "Tổng số nốt hai lần tung bằng i" (i = 1, 6)

    Nj,k: "Số nốt trên lần tung thứ j bằng k" (j = 1, 2; k = 1, 6)

    Ta tìm

    P\left( T_{i}|N_{1,2} \cup N_{1,4} \cup N_{1,6} ight) = \frac{P\left( N_{1,2} \cup N_{2;2} ight)}{P\left(N_{1,2} \cup N_{1,4} \cup N_{1,6} ight)}= \dfrac{\left( \dfrac{1}{6}ight)^{2}}{\dfrac{1}{2}} = \dfrac{1}{18}

  • Câu 5: Vận dụng cao
    Tính xác suất theo yêu cầu

    Một tổ có 15 sinh viên trong đó có 5 sinh viên học giỏi môn Toán. Cần chia làm 5 nhóm, mỗi nhóm 3 sinh viên. Tính xác suất để nhóm nào cũng có một sinh viên học giỏi môn Toán?

    Hướng dẫn:

    Gọi A_{i} là biến cố 'nhóm thứ i có 1 người giỏi Toán' và A là sự kiện nhóm nào cũng có người giỏi Toán, thì dễ dàng nhận thấy:

    A = A_{1}A_{2}A_{3}A_{4}A_{5}

    Ta có:

    P\left( A_{1} ight) = \frac{C_{5}^{1}C_{10}^{2}}{C_{15}^{3}} = \frac{45}{91}

    P\left( A_{2} \mid A_{1} ight) = \frac{C_{4}^{1}C_{8}^{2}}{C_{12}^{3}} = \frac{28}{55}

    P\left( A_{3} \mid A_{1}A_{2} ight) = \frac{C_{3}^{1}C_{6}^{2}}{C_{9}^{3}} = \frac{15}{28}

    P\left( A_{4} \mid A_{1}A_{2}A_{3} ight) = \frac{C_{2}^{1}C_{4}^{2}}{C_{6}^{3}} = \frac{3}{5}

    P\left( A_{5} \mid A_{1}A_{2}A_{3}A_{4} ight) = \frac{C_{1}^{1}C_{2}^{2}}{C_{3}^{3}} = 1

    Áp dụng công thức xác suất của tích ta có:

    P(A) = P\left( A_{1} ight)P\left( A_{2} \mid A_{1} ight)P\left( A_{3} \mid A_{1}A_{2} ight)P\left( A_{4} \mid A_{1}A_{2}A_{3} ight)P\left( A_{5} \mid A_{1}A_{2}A_{3}A_{4} ight)

    = \frac{C_{5}^{1}}{C_{15}^{3}} \cdot \frac{C_{4}^{2}}{C_{12}^{3}} \cdot \frac{C_{3}^{1}}{C_{9}^{3}} \cdot \frac{C_{2}^{1}}{C_{6}^{3}} \cdot \frac{C_{1}^{2}}{C_{3}^{3}} \simeq 0,0809

  • Câu 6: Thông hiểu
    Xét tính đúng sai của các khẳng định

    Năm 2012, Cộng đồng Châu Âu có làm một đợt kiểm tra rất rộng rãi các con bò để phát hiện những con bị bệnh bò điên. Người ta tiến hành một loại xét nghiệm và cho kết quả như sau: Khi con bò bị bệnh bò điên thì xác suất để ra phản ứng dương tính trong xét nghiệm là 60\%; còn khi con bò không bị bệnh thì xác suất để xảy ra phản ứng dương tính trong xét nghiệm đó là 20\%. Biết rằng ti lệ bò bị mắc bệnh bò điên ở Hà Lan là 1,5 con trên 100000 con. Gọi X là biến cố một con bò bị bệnh bò điên, Y là biến cố một con bò phản ứng dương tính với xét nghiệm.

    a) P(X) = 15.10^{- 6}. Đúng||Sai

    b) P(Y \mid X) = 0,06. Sai||Đúng

    c) P\left( Y \mid \overline{X} ight) = 0,2. Đúng||Sai

    d) P(Y \cap X) = 9.10^{- 7}. Sai||Đúng

    Đáp án là:

    Năm 2012, Cộng đồng Châu Âu có làm một đợt kiểm tra rất rộng rãi các con bò để phát hiện những con bị bệnh bò điên. Người ta tiến hành một loại xét nghiệm và cho kết quả như sau: Khi con bò bị bệnh bò điên thì xác suất để ra phản ứng dương tính trong xét nghiệm là 60\%; còn khi con bò không bị bệnh thì xác suất để xảy ra phản ứng dương tính trong xét nghiệm đó là 20\%. Biết rằng ti lệ bò bị mắc bệnh bò điên ở Hà Lan là 1,5 con trên 100000 con. Gọi X là biến cố một con bò bị bệnh bò điên, Y là biến cố một con bò phản ứng dương tính với xét nghiệm.

    a) P(X) = 15.10^{- 6}. Đúng||Sai

    b) P(Y \mid X) = 0,06. Sai||Đúng

    c) P\left( Y \mid \overline{X} ight) = 0,2. Đúng||Sai

    d) P(Y \cap X) = 9.10^{- 7}. Sai||Đúng

    Tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 1,5 con trên 100\ 000 con nghĩa là P(X) = 15.10^{- 6}.

    Khi con bò bị bệnh bò điên, thì xác suất để ra phản ứng dương tính trong xét nghiệm là 60%, nghĩa là: P\left( Y|X ight) = 0,6.

    Khi con bò không bị bệnh, thì xác xuất để xả ra phản ứng dương tính trong xét nghiệm đó là 20%, nghĩa là P\left( Y|\overline{X} ight) = 0,2. Khi đó, ta có:

    P(Y \cap X) = P\left( Y|X ight).P(X) = 0,6\ .\ 15\ .\ 10^{- 6} = 9.10^{- 6}.

  • Câu 7: Vận dụng
    Tính xác suất có điều kiện

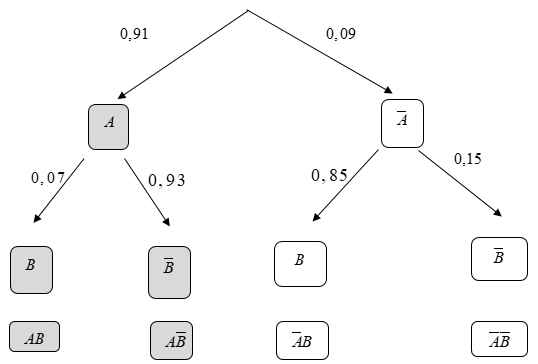
    Trong một kỳ thi, có 60% học sinh đã làm đúng bài toán đầu tiên và 40% học sinh đã làm đúng bài toán thứ hai. Biết rằng có 20% học sinh làm đúng cả hai bài toán. Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là bao nhiêu?

    Hướng dẫn:

    Ta có:

    A: "học sinh đã làm đúng bài toán đầu tiên", thì P(A) = 60\% = 0,6.

    B: "học sinh đã làm đúng bài toán thứ hai", thì P(B) = 40\% = 0,4.

    A \cap B: "học sinh làm đúng cả hai bài toán", thì P(A \cap B) = 20\% = 0,2.

    Xác suất để một học sinh làm đúng bài toán thứ hai biết rằng học sinh đó đã làm đúng bài toán đầu tiên là P\left( B|A \right) = \frac{P(A \cap B)}{P(A)} = \frac{0,2}{0,6} = \frac{1}{3} \approx 0.33.

  • Câu 8: Vận dụng
    Xét tính đúng sai của các phương án

    Một công ty truyền thông đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là 0,5 và dự án 2 là 0,6. Khả năng thắng thầu của 2 dự án là 0,4. Gọi A;B lần lượt là biến cố thắng thầu dự án 1 và dự án 2.

    a) A;B là hai biến độc lập. Đúng||Sai

    b) Xác suất công ty thắng thầu đúng 1 dự án là 0,3. Đúng||Sai

    c) Biết công ty thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là 0,4. Sai|| Đúng

    d) Biết công ty không thắng thầu dự án 1, xác suất công ty thắng thầu dự án 0,8. Sai|| Đúng

    Đáp án là:

    Một công ty truyền thông đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là 0,5 và dự án 2 là 0,6. Khả năng thắng thầu của 2 dự án là 0,4. Gọi A;B lần lượt là biến cố thắng thầu dự án 1 và dự án 2.

    a) A;B là hai biến độc lập. Đúng||Sai

    b) Xác suất công ty thắng thầu đúng 1 dự án là 0,3. Đúng||Sai

    c) Biết công ty thắng thầu dự án 1, xác suất công ty thắng thầu dự án 2 là 0,4. Sai|| Đúng

    d) Biết công ty không thắng thầu dự án 1, xác suất công ty thắng thầu dự án 0,8. Sai|| Đúng

    Ta có:\left\{ \begin{matrix} P(A) = 0,5 \Rightarrow P\left( \overline{A} ight) = 1 - 0,5 = 0,5 \\ P(B) = 0,6 \Rightarrow P\left( \overline{B} ight) = 1 - 0,6 = 0,4 \\ P(A \cap B) = 0,4 \\ \end{matrix} ight.

    a) A;B là hai biến cố độc lập khi và chỉ khi P(A \cap B) = P(A).P(B)

    Mà 0,4 eq 0,5.0,6 nên A;B không độc lập.

    b) Gọi C là biến cố thắng thầu đúng 1 dự án

    P(C) = P\left( A \cap \overline{B} ight) + P\left( \overline{A} \cap B ight)

    = P(A) - P(A \cap B) + P(B) - P(A \cap B)

    = P(A) + P(B) - 2P(A \cap B)

    = 0,5 + 0.6 - 2.0,4 = 0,3.

    c) Gọi D là biến cố thắng dự 2 biết thắng dự án 1

    P(D) = P\left( B|A ight) = \frac{P(B \cap A)}{P(A)} = \frac{0,4}{0,5} = 0,8.

    d) Gọi E là biến cố “thắng dự án 2 biết không thắng dự án 1”

    P(E) = P\left( B|\overline{A} ight) = \frac{P(B) - P(A \cap B)}{P\left( \overline{A} ight)} = \frac{0,6 - 0,4}{0,5} = 0,4.

  • Câu 9: Vận dụng cao
    Tính xác suất bắn trúng

    Cuối tuần M đến sân chơi để bắn cung, biết khoảng cách bắn tên thay đổi liên tục và khả năng bạn M bắn trúng bia tỉ lệ nghịch với khoảng cách bắn. M bắn lần đầu ở khoảng cách 20m với xác suất trúng bia là 0,5, nếu bị trượt M bắn tiếp mũi tên thứ hai ở khoảng cách 30m, nếu lại trượt M bắn mũi tên thứ ba ở khoảng cách 40m. Tính xác suất để M bắn trúng bia?

    Hướng dẫn:

    Gọi A là biến cố “M bắn trúng bia ở lần thứ nhất”

    Gọi B là biến cố “M bắn trúng bia ở lần thứ hai”

    Gọi C là biến cố “M bắn trúng bia ở lần thứ ba”

    Ta có: P(A) = 0,5

    Vì xác suất bắn trúng bia trong mỗi lần bắn tỷ lệ nghịch với khoảng cách bắn nên ta có:

    \left\{ \begin{matrix}P\left( B|\overline{A} ight) = \dfrac{20.0,5}{30} = \dfrac{1}{3} \\P\left( C|\overline{A}.\overline{B} ight) = \dfrac{20.0,5}{40} =\dfrac{1}{4} \\\end{matrix} ight.

    Ta có sơ đồ cây như sau:

    Xác suất để M bắn trúng bia là:

    P(A) + P\left( \overline{A}B ight) + P\left( \overline{A}\overline{B}C ight) = 0,5 + 0,5.\frac{1}{3} + 0,5.\frac{2}{3}.\frac{1}{4} = 0,75

  • Câu 10: Vận dụng
    Tìm giá trị xác suất

    Một tập gồm 10 chứng từ, trong đó có 2 chứng từ không hợp lệ. Một cán bộ kế toán rút ngẫu nhiên 1 chứng từ và tiếp đó rút ngẫu nhiên 1 chứng từ khác để kiểm tra. Tính xác suất để cả 2 chứng từ rút ra đều hợp lệ?

    Hướng dẫn:

    Gọi A là biến cố cả 2 chứng từ rút ra đều hợp lệ

    B là biến cố trong 3 chứng từ rút ra, chỉ có chứng từ thứ 3 không hợp lệ.

    Theo yêu cầu của đầu bài ta phải tính xác xác suất P(A), P(B).

    Nếu gọi Ai là biến cố chứng từ rút ra lần thứ i là hợp lệ} (i = 1,3).

    Khi đó ta có: A = A_1 . A_2 và B = A_1 . A_2 . A_3

    Vì vậy các xác suất cần tìm là:

    P(A) = P\left( A_{1}.\ A_{2} ight) = P\left( A_{1} ight).P\left( A_{2}|A_{1} ight) = \frac{8}{10}.\frac{7}{9} = \frac{28}{45}

    P(B) = P\left( A_{1}.\ A_{2}.\overline{A_{3}} ight)

    = P\left( A_{1} ight).P\left( A_{2}|A_{1} ight).P\left( \overline{A_{3}}|A_{1}.\ A_{2} ight)

    = \frac{8}{10}.\frac{7}{9}.\frac{2}{8} = \frac{7}{45}

  • Câu 11: Thông hiểu
    Tính xác suất của biến cố

    Cho một hộp kín có 6 thẻ ATM của ACB và 4 thẻ ATM của Vietcombank. Lấy ngẫu nhiên lần lượt 2 thẻ (lấy không hoàn lại). Tìm xác suất để lần thứ hai lấy được thẻ ATM của Vietcombank nếu biết lần thứ nhất đã lấy được thẻ ATM của ACB.

    Hướng dẫn:

    Gọi A là biến cố “lần thứ hai lấy được thẻ ATM Vietcombank”, B là biến cố “lần thứ nhất lấy được thẻ ATM của ACB”.

    Ta cần tìm Ρ\left( A|B \right).

    Sau khi lấy lần thứ nhất (biến cố B xảy ra) trong hộp còn lại 9 thẻ (trong đó có 4 thẻ Vietcombank) nên Ρ\left( A|B \right) = \frac{4}{9}.

  • Câu 12: Vận dụng cao
    Ghi đáp án vào ô trống

    Một xí nghiệp mỗi ngày sản xuất ra 1000 sản phẩm trong đó có 15 sản phẩm lỗi. Lần lượt lấy ra ngẫu nhiên hai sản phẩm không hoàn lại để kiểm tra. Tính xác suất của biến cố: Sản phẩm lấy ra lần thứ hai bị lỗi (làm tròn kết quả đến hàng phần trăm).

    Đáp án: 0,02

    Đáp án là:

    Một xí nghiệp mỗi ngày sản xuất ra 1000 sản phẩm trong đó có 15 sản phẩm lỗi. Lần lượt lấy ra ngẫu nhiên hai sản phẩm không hoàn lại để kiểm tra. Tính xác suất của biến cố: Sản phẩm lấy ra lần thứ hai bị lỗi (làm tròn kết quả đến hàng phần trăm).

    Đáp án: 0,02

    Xét các biến cố:

    A_{1}: Sản phẩm lấy ra lần thứ nhất bị lỗi.

    Khi đó, ta có: P\left( A_{1} ight) = \frac{15}{1000}; P\left( \overline{A_{1}} ight) = \frac{197}{200}.

    A_{2}: Sản phẩm lấy ra lần thứ hai bị lỗi.

    Khi sản phẩm lấy ra lần thứ nhất bị lỗi thì còn 999 sản phẩm và trong đó có 14 sản phẩm lỗi nên ta có: P\left( A_{2}\left| A_{1} ight.\ ight) = \frac{14}{999}, suy ra P\left( \overline{A_{2}}\left| A_{1} ight.\ ight) = \frac{985}{999}.

    Khi sản phẩm lấy ra lần thứ nhất không bị lỗi thì còn 999 sản phẩm trong đó có 15sản phẩm lỗi nên ta có: P\left( A_{2}\left| \overline{A_{1}} ight.\ ight) = \frac{15}{999}, suy ra P\left( \overline{A_{2}}\left| \overline{A_{1}} ight.\ ight) = \frac{328}{333}.

    Khi đó, xác suất để sản phẩm lấy ra lần thứ hai bị lỗi là:

    P\left( A_{2} ight) = P\left( A_{2}\left| A_{1} ight.\ ight).P\left( A_{1} ight) + P\left( A_{2}\left| \overline{A_{1}} ight.\ ight).P\left( \overline{A_{1}} ight)

    = \frac{14}{999}.\frac{15}{1000} + \frac{15}{999}.\frac{197}{200} \approx 0,02.

    Đáp số: 0,02.

  • Câu 13: Vận dụng
    Chọn đáp án đúng

    Một nhóm học sinh có 20 học sinh, trong đó có 12 em thích học môn Toán, 10 em thích học môn Văn, 2 em không thích học cả hai môn Toán và Văn. Chọn ngẫu nhiên 1 học sinh, xác xuất để học sinh đó thích học môn Toán biết rằng học sinh đó thích học môn Văn là

    Hướng dẫn:

    Gọi A là biến cố “học sinh đó thích học môn Toán”,

    B là biến cố “học sinh đó thích học môn Văn”

    Xác suất để học sinh được chọn thích học môn Toán, biết học sinh đó thích học môn Văn chính là P\left( A|B \right).

    Ta có P(A) = \frac{12}{20} = \frac{3}{5}, P(B) = \frac{10}{20} = \frac{1}{2}, P\left( \overline{A}\ \overline{B} \right) = \frac{2}{20} = \frac{1}{10}

    P(A \cup B) = 1 - P\left( \overline{A}\ \overline{B} \right) = 1 - \frac{1}{10} = \frac{9}{10}

    Ta có P(AB) = P(A) + P(B) - P(A \cup B) = \frac{3}{5} + \frac{1}{2} - \frac{9}{10} = \frac{1}{5}

    P\left( A|B \right) = \frac{P(AB)}{P(B)} = \frac{1}{5}:\frac{1}{2} = \frac{2}{5}

  • Câu 14: Vận dụng
    Ghi đáp án vào ô trống

    Câu lạc bộ thể thao của trường Việt Anh có 40 bạn đều biết chơi biết chơi ít nhất một trong hai môn là bóng đá và cầu lông, trong đó có 27 bạn biết chơi bóng đá và 25 bạn biết chơi cầu lông. Chọn ngẫu nhiên 1 bạn. Xác suất chọn được bạn biết chơi bóng đá biết bạn đó chơi được cầu lông là bao nhiều?

    Đáp án: 0,48

    Đáp án là:

    Câu lạc bộ thể thao của trường Việt Anh có 40 bạn đều biết chơi biết chơi ít nhất một trong hai môn là bóng đá và cầu lông, trong đó có 27 bạn biết chơi bóng đá và 25 bạn biết chơi cầu lông. Chọn ngẫu nhiên 1 bạn. Xác suất chọn được bạn biết chơi bóng đá biết bạn đó chơi được cầu lông là bao nhiều?

    Đáp án: 0,48

    Xét các biến cố: A: “Chọn được bạn biết chơi bóng đá”

    B: “Chọn được bạn biết chơi cầu lông”

    Khi đó P(A) = \frac{27}{40} = 0,675; P(B) = \frac{25}{40} = 0,625; P(A \cup B) = 1.

    Suy ra P(A \cap B) = P(A) + P(B) - P(A \cup B) = 0,675 + 0,625 - 1 = 0,3.

    Vậy xác suất chọn được bạn biết chơi bóng đá, bạn đó biết chơi cầu lông là P\left( A|B ight) = \frac{P(A \cap B)}{P(B)} = \frac{0,3}{0,625} = 0,48.

    Đáp số: 0,48.

  • Câu 15: Thông hiểu
    Xác định công thức đúng

    Cho ba biến cố A;B;C độc lập từng đôi thỏa mãn P(A) = P(B) = P(C) = p và P(ABC) = 0. Xác định P\left( \overline{A}\overline{B}\overline{C} ight)?

    Hướng dẫn:

    Ta có:

    P\left( A\overline{B}\overline{C} ight) = P\left( A\overline{B} ight) - P\left( A\overline{B}C ight)

    = p(1 - p) - p^{2} = p - 2p^{2}

    Vì A, B, C có vai trò như nhau nên P\left( A\overline{B}C ight) = P\left( AB\overline{C} ight)

    \Rightarrow P\left( \overline{A}\overline{B}\overline{C} ight) = P\left( \overline{B}\overline{C} ight) - P\left( A\overline{B}\overline{C} ight)

    = (1 - p)^{2} - p - 2p^{2} = 3p^{2} - 3p + 1

  • Câu 16: Vận dụng
    Ghi đáp án vào ô trống

    Một bệnh truyền nhiễm có xác suất lây bệnh là 0,8 nếu tiếp xúc với người bệnh mà không đeo khẩu trang; là 0,1 nếu tiếp xúc với người bệnh mà có đeo khẩu trang. Chị Mai có tiếp xúc với người bệnh hai lần, một lần đeo khẩu trang và một lần không đeo khẩu trang. Tính xác suất để chị Mai bị lây bệnh từ người bệnh truyền nhiễm đó. (Kết quả ghi dưới dạng số thập phân).

    Đáp án: 0,82

    Đáp án là:

    Một bệnh truyền nhiễm có xác suất lây bệnh là 0,8 nếu tiếp xúc với người bệnh mà không đeo khẩu trang; là 0,1 nếu tiếp xúc với người bệnh mà có đeo khẩu trang. Chị Mai có tiếp xúc với người bệnh hai lần, một lần đeo khẩu trang và một lần không đeo khẩu trang. Tính xác suất để chị Mai bị lây bệnh từ người bệnh truyền nhiễm đó. (Kết quả ghi dưới dạng số thập phân).

    Đáp án: 0,82

    Gọi A là biến cố: "Chị Hoa bị nhiễm bệnh khi tiếp xúc người bệnh mà không đeo khẩu trang" và B : "Chị Hoa bị nhiễm bệnh khi tiếp xúc với người bệnh dù có đeo khẩu trang”.

    Dễ thấy \overline{A},\overline{B} là hai biến cố độc lập.

    Xác suất để chị Hoa không nhiễm bệnh trong cả hai lần tiếp xúc với người bệnh là

    P(\overline{A}\overline{B}) = P(\overline{A}) \cdot P(\overline{B}) = 0,2 \cdot 0,9 = 0,18.

    Gọi P là xác suất để chị Hoa bị lây bệnh khi tiếp xúc người bệnh, ta có:

    P = 1 - P(\overline{A}\overline{B}) = 1 - 0,18 = 0,82.

  • Câu 17: Vận dụng cao
    Tính xác suất có điều kiện

    Trong một đội tuyển có ba vận động viên A,\ \ B và C thi đấu với xác suất chiến thắng lần lượt là 0,6;\ \ 0,7 và 0,8. Giả sử mỗi người thi đấu một trận độc lập với nhau. Tính xác suất để A thua trong trường hợp đội tuyển thắng hai trận.

    Hướng dẫn:

    Gọi A là biến cố “vận động viên A chiến thắng”, ta có P(A) = 0,6;

    B là biến cố “vận động viên B chiến thắng” thì P(B) = 0,7;

    C là biến cố “vận động viên C chiến thắng” thì P(C) = 0,8.

    Gọi D là biến cố “đội tuyển thắng hai trận”. Ta có

    P(D) = P\left( AB\overline{C} \right) + P\left( A\overline{B}C \right) + P\left( \overline{A}BC \right) = 0,452.

    Vậy xác suất cần tính là

    P\left(\overline{A}\left| D \right.\ \right) = \frac{P\left( \overline{A}D\right)}{P(D)} = \frac{P\left( \overline{A}BC \right)}{P(D)}=\frac{0,4.0,7.0,8}{0,452} = \frac{56}{113}.

  • Câu 18: Vận dụng cao
    Chọn kết quả chính xác

    Để thành lập đội tuyển quốc gia về một môn học, người ta tổ chức một cuộc thi tuyển gồm 3 vòng. Vòng thứ nhất lấy 80\% thí sinh; vòng thứ hai lấy 70\% thí sinh đã qua vòng thứ nhất và vòng thứ ba lấy 45\% thí sinh đã qua vòng thứ hai. Để vào được đội tuyển, thí sinh phải vượt qua được cả 3 vòng thi. Tính xác suất để một thí sinh bất kỳ bị loại ở vòng thứ hai, biết rằng thí sinh này bị loại?

    Hướng dẫn:

    Gọi A_{i} là "thí sinh vượt qua vòng thứ i ' thì ta có P\left( A_{1} ight) = 0,8,P\left( A_{2} \mid A_{1} ight) = 0,7 và P\left( A_{3} \mid A_{1}A_{2} ight) = 0,45

    Gọi A là biến cố thí sinh được vào đội tuyển thì A xảy ra nếu thí sinh vượt qua cả 3 vòng, nghĩa là A = A_{1}A_{2}A_{3}

    P(A) = P\left( A_{1}A_{2}A_{3} ight) = P\left( A_{1} ight)P\left( A_{2} \mid A_{1} ight)P\left( A_{3} \mid A_{1}A_{2} ight)= 0,8.0,7.0,45 = 0,252

    Gọi C là biến cố "thí sinh bị loại ở vòng 2, biết thí sinh này bị loại'.

    Ta biểu diễn C = A_{1}\overline{A_{2}} \mid \bar{A}.

    P(C) = \frac{P\left\lbrack \left(A_{1}\overline{A_{2}} ight)\bar{A} ightbrack}{P(\bar{A})} =\frac{P\left( A_{1}\overline{A_{2}} ight)}{P(\bar{A})} vì A_{1}\overline{A_{2}} \subset \bar{A}

    = \frac{P\left( A_{1} ight)P\left( \overline{A_{2}} \mid A_{1} ight)}{P(\bar{A})}= \frac{0,8.(1 - 0,7)}{1 - 0,252} \simeq 0,3208

  • Câu 19: Vận dụng
    Tính xác suất của biến cố

    Chọn ngẫu nhiên lần lượt các số a, b phân biệt thuộc tập hợp \left\{ 3^{k} \mid k \in N,1 \leq k \leq 10 ight\}. Tính xác suất để \log_{a}b là một số nguyên dương.

    Gợi ý:

    Sử dụng công thức tính xác suất xảy ra biến cố A:P(A) = \frac{n_{A}}{n_{\Omega}}.

    Hướng dẫn:

    Phép thử: "Chọn ngẫu nhiên lần lượt các số a, b phân biệt thuộc tập hợp \left\{ 3^{k} \mid k \in N,1 \leq k \leq 10 ight\}

    Biến cố A: "\log_{a}b là một số nguyên dương".

    \Rightarrow n_{\Omega} = 10.9 = 90

    + Giả sử a = 3^{k_{1}},b = 3^{k_{2}}\left( k_{1} eq k_{2} ight) \Rightarrow log_{a}b = log_{3^{k_{1}}}\left( 3^{k_{2}} ight) = \frac{k_{2}}{k_{1}} là một số nguyên dương

    k_{2}

    10

    9

    8

    7

    6

    5

    4

    3

    2
    k_{1} 1;2;5 1;3 1;2;4

    1

    		 1;2;3

    1

    1;2

    1

    1

    \Rightarrow n_{A} = 17 \Rightarrow P(A) = \frac{n_{A}}{n_{\Omega}} = \frac{17}{90}.

  • Câu 20: Vận dụng cao
    Tính xác suất của biến cố

    Một bài trắc nghiệm có 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn trong đó có 1 đáp án đúng được 5 điểm và mỗi câu trả lời sai bị trừ đi 2 điểm. Một học sinh không học bài nên đánh hàng loạt một câu trả lời. Tìm xác suất để học sinh này nhận điểm dưới 1.

    Gợi ý:

    Tìm xác suất để học sinh trả lời câu đúng và câu sai.

    Gọi x là câu trả lời đúng. Từ đó tính số điểm học sinh đạt được theo x.

    Từ giả thiết học sinh được điểm dưới 1 tìm x

    Từ đó sử dụng quy tắc cộng xác suất để tìm xác suất của bài toán

    Hướng dẫn:

    Xác suất để học sinh trả lời đúng 1 câu là \frac{1}{4} và trả lời sai 1 câu là \frac{3}{4}.

    Gọi x là số câu trả lời đúng \Rightarrow 10 - x là số câu trả lời sai.

    Số điểm học sinh đạt được là: 5x - 2.(10 - x) = 7x - 20

    Học sinh nhận được điểm dưới 1 khi 7x - 20 < 1 \Leftrightarrow x < 3

    Mà x\mathbb{\in Z \Rightarrow}x \in \{ 0;1;2\}

    Gọi A_{i}(i = 0,1,2) là biến cố: "Học sinh trả lời đúng i câu"

    A là biến cố "Học sinh nhận điểm dưới 1"

    Suy ra A = A_{0} \cup A_{1} \cup A_{2} và P(A) = P\left( A_{0}ight) + P\left( A_{1} ight) + P\left( A_{2} ight)

    Mà P\left( A_{i} ight) = C_{10}^{i}.\left( \frac{1}{4} ight)^{i}.\left( \frac{3}{4} ight)^{10 - i} nên P(A) = \sum_{i = 0,}^{2}C_{10}^{i}.\left( \frac{1}{4} ight)^{i}.\left( \frac{3}{4} ight)^{10 - i} = 0,5256

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (25%):
    2/3
  • Thông hiểu (45%):
    2/3
  • Vận dụng (30%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
1
18 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Trắc nghiệm Toán 12 Kết nối tri thức
Xem thêm