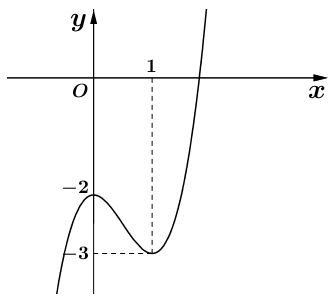
Cho hàm số xác định, liên tục trên R và có bảng biến thiên như hình vẽ dưới đây:
Xét tính đúng sai của các khẳng định sau:
a) Hàm số đồng biến trên khoảng . Sai|| Đúng
b) Hàm số đạt cực đại tại điểm . Đúng||Sai
c) Hàm số có giá trị nhỏ nhất bằng −2. Sai|| Đúng
d) Hàm số có giá trị lớn nhất bằng 5. Đúng||Sai
Cho hàm số xác định, liên tục trên R và có bảng biến thiên như hình vẽ dưới đây:
Xét tính đúng sai của các khẳng định sau:
a) Hàm số đồng biến trên khoảng . Sai|| Đúng
b) Hàm số đạt cực đại tại điểm . Đúng||Sai
c) Hàm số có giá trị nhỏ nhất bằng −2. Sai|| Đúng
d) Hàm số có giá trị lớn nhất bằng 5. Đúng||Sai
Hàm số không có giá trị nhỏ nhất nên phát biểu “Hàm số
có giá trị nhỏ nhất bằng −2” là phát biểu sai.