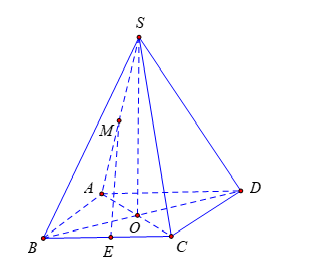
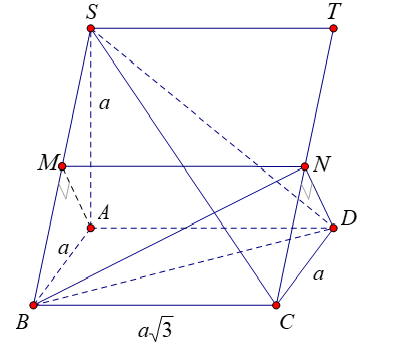
Cho hình chóp có đáy là hình thang vuông tại
và
, thỏa mãn điều kiện,
,
,
vuông góc với mặt đáy
,
. Gọi
lần lượt là trung điểm của
. Tính cosin của góc giữa
và
. (Làm tròn kết quả đến hàng phần trăm)
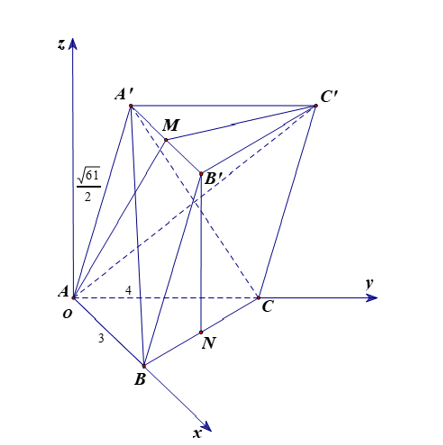
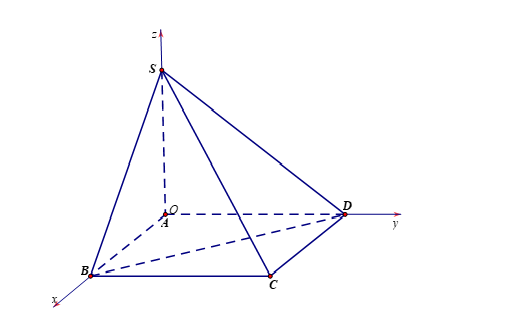
Chọn hệ trục tọa độ như hình vẽ
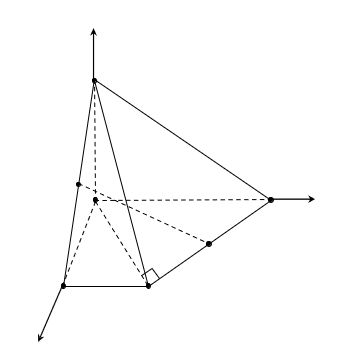
Chọn đơn vị là a
Có
Vecto chỉ phương của là
Vecto pháp tuyến của là
Vậy
Suy ra: