Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:

Ta có: và
nên tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:

Ta có: và
nên tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm
Thống kê đường kính thân gỗ của một số cây xoan đào 7 năm tuổi được trồng ở một lâm trường ở bảng 1.
|
Đường kính |
|||||
|
Tần số |
5 |
20 |
18 |
7 |
3 |
Hãy tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên.
Khoảng biến thiên của mẫu số liệu ghép nhóm là
Bảng sau thống kê cân nặng của 50 quả xoài được lựa chọn ngẫu nhiên sau khi thu hoạch ở một nông trường.
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Khoảng biên thiên bằng
Xét mẫu số liệu ghép nhóm cho bởi Bảng 1.
|
Nhóm |
Tần số |
|
… |
… |
Khoảng biến thiên của mẫu số liệu ghép nhóm đó bằng?
Khoảng biến thiên của mẫu số liệu ghép nhóm đó bằng .
Cho bảng thống kê thời gian (đơn vị: phút) và số ngày tập thể dục của hai người A và B trong 30 ngày như sau:
|
Thời gian |
[15; 20) |
[25; 30) |
[30; 35) |
|
Số ngày tập của A |
10 |
15 |
5 |
|
Số ngày tập của B |
9 |
21 |
0 |
Chọn kết luận đúng dưới đây?
Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập của A là: 35 – 15 = 20 (phút).
Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập của B là: 30 – 15 = 15 (phút).
Do đó căn cứ theo khoảng biến thiên thì thời gian tập của A có độ phân tán lớn hơn.
Khảo sát thời gian nghe nhạc trong ngày của một số học sinh khối 12 thu được mẫu số liệu ghép nhóm sau:
|
Thời gian (phút) |
|||||
|
Số học sinh |
5 | 9 | 12 | 10 | 6 |
Nhóm chứa tứ phân vị thứ ba là
Gọi là mẫu số liệu gốc về thời gian nghe nhạc trong ngày của
học sinh khối 12 được xếp theo thứ tự tăng dần.
Tứ phân vị thứ ba là trung vị của dãy
,
,...,
nên
. Do đó
thuộc nhóm
.
Một ý nghĩa của khoảng tứ phân vị là
Ý nghĩa của khoảng tứ phân vị:
- Khoảng tứ phân vị của mẫu số liệu ghép nhóm xấp xỉ khoảng tứ phân vị của mẫu số liệu gốc và là một đại lượng cho biết mức độ phân tán của nửa giữa mẫu số liệu.
Cho mẫu số liệu ghép nhóm:
|
Nhóm |
Tần số |
|
(0;10] |
8 |
|
(10;20] |
14 |
|
(20;30] |
12 |
|
(30;40] |
9 |
|
(40;50] |
7 |
Tìm khoảng biến thiên?
Khoảng biến thiên của mẫu số liệu đã cho là: .
Bảng sau thống kê khối lượng một số quả quýt trong thùng hàng:
|
Khối lượng (gam) |
[80; 82) |
[82; 84) |
[84; 86) |
[86; 88) |
[88; 90) |
|
Số quả |
17 |
20 |
25 |
16 |
12 |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 90 – 80 = 10 gam.
Thống kê thời gian sử dụng mạng xã hội trong ngày của các bạn học sinh tổ 1 và tổ 2 lớp 12A thu được bảng sau:

Tìm khoảng biến thiên cho thời gian sử dụng mạng xã hội của tổ 1 và tổ 2.
Khoảng biến thiên cho thời gian sử dụng mạng xã hội của tổ 1 là
Khoảng biến thiên cho thời gian sử dụng mạng xã hội của tổ 2 là
Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khoẻ. Quãng đường đi bộ mỗi ngày (đơn vị: ) của bác Hương trong 20 ngày được thống kê lại ở bảng sau:

Khoảng biến thiên của mẫu số liệu ghép nhóm là
Khoảng biến thiên của mẫu số liệu ghép nhóm là:
Điểm kiểm tra của nhóm học sinh lớp 10 được cho như sau:
|
Lớp điểm |
[3;4] |
[5;6] |
[7;8] |
[9;10] |
|
Số học sinh |
3 |
3 |
2 |
2 |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Ta có khoảng biến thiên của mẫu số liệu trên là
Biểu đồ sau biểu diễn tốc độ tăng trưởng GDP của Nhật Bản trong giai đoạn 1990 đến 2005. Hãy tìm khoảng biến thiên của mẫu số liệu đó.
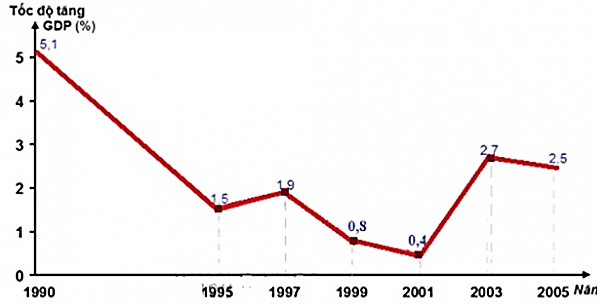
Ta có giá trị lớn nhất của mẫu số liệu là 5,1 và giá trị nhỏ nhất của mẫu số liệu là 0,4
⇒ R = 5,1 – 0,4 = 4,7.
Bạn Lan thống kê lại chiều cao (đơn vị: cm) của các học sinh nữ lớp 12B và lớp 12C ở bảng sau.
|
Chiều cao(cm) |
[150; 155) |
[155; 160) |
[160; 165) |
[165; 170) |
[175; 180) |
|
Số học sinh nữ lớp 12B |
0 |
5 |
13 |
7 |
0 |
|
Số học sinh nữ lớp 12C |
2 |
10 |
9 |
3 |
1 |
Chọn đáp án có khẳng định đúng.
Ta có
Khoảng biến thiên của mẫu số liệu ghép nhóm về chiều cao của các bạn nữ lớp 12B là 170 - 155 = 15
Khoảng biến thiên của mẫu số liệu ghép nhóm về chiều cao của các bạn nữ lớp 12C là 175 – 150 = 25
Vì 15 < 25 nên mẫu số liệu ghép nhóm về chiều cao của các bạn nữ lớp 12B có độ phân tán ít hơn so với mẫu số liệu ghép nhóm về chiều cao của các bạn nữ lớp 12C, hay nói cách khác chiều cao của các bạn nữ lớp 12B đồng đều hơn chiều cao của các bạn nữ lớp 12C.
Bác Hùng thống kê lại đường kính thân gỗ của một số cây Keo tai tượng 5 năm tuổi được trồng ở một lâm trường ở bảng sau.
|
Đường kính (cm) |
|
|
|
|
|
|
Số cây |
5 |
20 |
18 |
7 |
3 |
Hãy tìm số trung bình cộng của mẫu số liệu ghép nhóm trên.
Ta có:
|
Đường kính (cm) |
|
|
|
|
|
|
Số cây |
5 |
20 |
18 |
7 |
3 |
|
Giá trị đại diện |
Số trung bình cộng:
Công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm là
Công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
Cho mẫu số liệu ghép nhóm có cùng đơn vị.
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đo mức độ phân tán của mẫu số liệu đó. Đúng||Sai
b) Khoảng biến thiên càng lớn thì mẫu số liệu càng ít phân tán. Sai||Đúng
c) Khoảng biến thiên của mẫu số liệu ghép nhóm không bị ảnh hưởng bởi các giá trị bất thường. Sai||Đúng
d) Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc. Đúng||Sai
Cho mẫu số liệu ghép nhóm có cùng đơn vị.
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đo mức độ phân tán của mẫu số liệu đó. Đúng||Sai
b) Khoảng biến thiên càng lớn thì mẫu số liệu càng ít phân tán. Sai||Đúng
c) Khoảng biến thiên của mẫu số liệu ghép nhóm không bị ảnh hưởng bởi các giá trị bất thường. Sai||Đúng
d) Khoảng biến thiên của mẫu số liệu ghép nhóm xấp xỉ cho khoảng biến thiên của mẫu số liệu gốc. Đúng||Sai
|
a) Đúng |
b) Sai |
c) Sai |
d) Đúng |
Câu a) Đúng.
Câu b) Sai – Do khoảng biến thiên càng lớn thì mẫu số liệu ghép nhóm càng phân tán.
Câu c) Sai – Do khoảng biến thiên chỉ sử dụng hai giá trị và
của mẫu số liệu nên dễ bị ảnh hưởng bởi các giá trị bất thường.
Câu d) Đúng.
Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau:
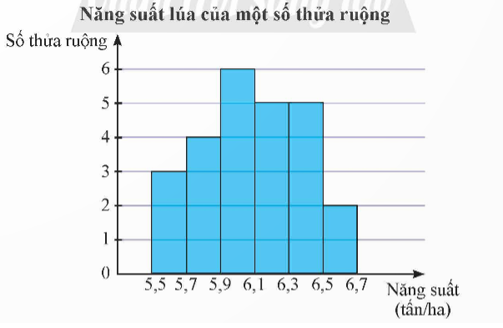
a) Có 6 thửa ruộng đã được khảo sát. Sai||Đúng
b) Khoảng biến thiên của mẫu số liệu trên là 1,2 (tấn/ha). Đúng||Sai
c) Khoảng tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là . Đúng||Sai
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là . Đúng||Sai
Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau:

a) Có 6 thửa ruộng đã được khảo sát. Sai||Đúng
b) Khoảng biến thiên của mẫu số liệu trên là 1,2 (tấn/ha). Đúng||Sai
c) Khoảng tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là . Đúng||Sai
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là . Đúng||Sai
|
A. |
B. |
C. |
D. |
|
SAI |
ĐÚNG |
ĐÚNG |
ĐÚNG |
a) Số thửa ruộng được khảo sát là: n = 3 + 4 + 6 + 5 + 5 + 2 = 25.
b) Từ biểu đồ, ta có bảng tần số ghép nhóm của mẫu số liệu như sau:
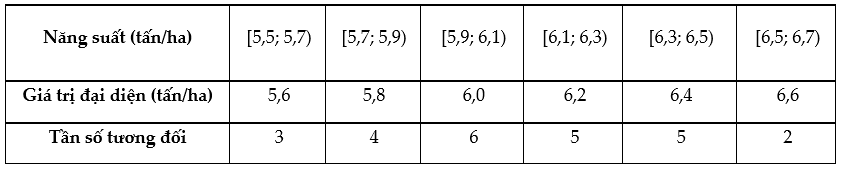
Khoảng biến thiên của mẫu số liệu đã cho là: R = 6,7 – 5,5 = 1,2 (tấn/ha).
c) Cỡ mẫu n = 25.
Gọi là mẫu số liệu gốc về năng suất của một số thửa ruộng được khảo sát được xếp theo thứ tự không giảm.
Ta có
[5,5; 5,7),
[5,7; 5,9),
[5,9; 6,1),
[6,1; 6,3),
[6,3; 6,5),
[6,5; 6,7).
Tứ phân vị thứ nhất của mẫu số liệu gốc là [5,7; 5,9).
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
d) Tứ phân vị thứ ba của mẫu số liệu gốc là [6,3; 6,5).
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
Cho mẫu dữ liệu ghép nhóm như sau:
|
Đối tượng |
Tần số |
|
[150; 155) |
15 |
|
[155; 160) |
10 |
|
[160; 165) |
40 |
|
[165; 170) |
27 |
|
[170; 175) |
5 |
|
[175; 180) |
3 |
Tính khoảng tứ phân vị của mẫu số liệu đã cho?
Ta có:
|
Đối tượng |
Tần số |
Tần số tích lũy |
|
[150; 155) |
15 |
15 |
|
[155; 160) |
11 |
26 |
|
[160; 165) |
39 |
65 |
|
[165; 170) |
27 |
92 |
|
[170; 175) |
5 |
97 |
|
[175; 180) |
3 |
100 |
Cỡ mẫu là:
=> tứ phân vị thứ nhất thuộc nhóm [155; 160) (vì 25 nằm giữa hai tần số tích lũy 15 và 26)
Do đó:
Khi đó tứ phân vị thứ nhất là:
Cỡ mẫu là:
=> tứ phân vị thứ ba nhóm [165; 170) (vì 75 nằm giữa hai tần số tích lũy 65 và 92)
Do đó:
Khi đó tứ phân vị thứ ba là:
Vậy khoảng tứ phân vị của mẫu số liệu là
Cô Hà thống kê lại đường kính thân gỗ của một số cây xoan đào 6 năm tuổi được trồng ở một lâm trường ở bảng sau.

Hãy tìm khoảng biến thiên của mẫu số liệu ghép nhóm trên.
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

