Đáp án là:
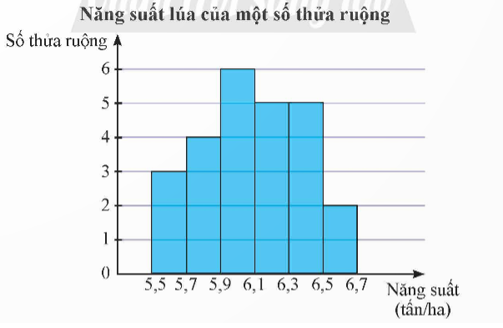
Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau:

a) Có 6 thửa ruộng đã được khảo sát. Sai||Đúng
b) Khoảng biến thiên của mẫu số liệu trên là 1,2 (tấn/ha). Đúng||Sai
c) Khoảng tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là  . Đúng||Sai
. Đúng||Sai
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là  . Đúng||Sai
. Đúng||Sai
|
A.
|
B.
|
C.
|
D.
|
|
SAI
|
ĐÚNG
|
ĐÚNG
|
ĐÚNG
|
a) Số thửa ruộng được khảo sát là: n = 3 + 4 + 6 + 5 + 5 + 2 = 25.
b) Từ biểu đồ, ta có bảng tần số ghép nhóm của mẫu số liệu như sau:
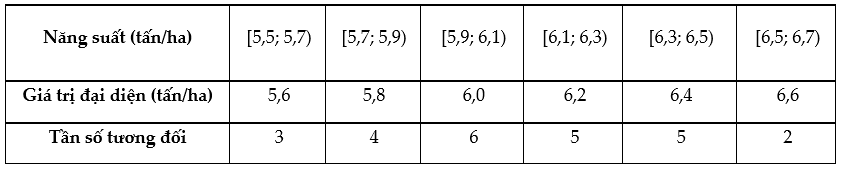
Khoảng biến thiên của mẫu số liệu đã cho là: R = 6,7 – 5,5 = 1,2 (tấn/ha).
c) Cỡ mẫu n = 25.
Gọi  là mẫu số liệu gốc về năng suất của một số thửa ruộng được khảo sát được xếp theo thứ tự không giảm.
là mẫu số liệu gốc về năng suất của một số thửa ruộng được khảo sát được xếp theo thứ tự không giảm.
Ta có
 [5,5; 5,7),
[5,5; 5,7),
 [5,7; 5,9),
[5,7; 5,9),
 [5,9; 6,1),
[5,9; 6,1),
 [6,1; 6,3),
[6,1; 6,3),
 [6,3; 6,5),
[6,3; 6,5),
 [6,5; 6,7).
[6,5; 6,7).
Tứ phân vị thứ nhất của mẫu số liệu gốc là  [5,7; 5,9).
[5,7; 5,9).
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: %20%3D%205%2C8625)
d) Tứ phân vị thứ ba của mẫu số liệu gốc là  [6,3; 6,5).
[6,3; 6,5).
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
%7D%7B5%7D(6%2C5-%206%2C3)%20%3D%206%2C33)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: