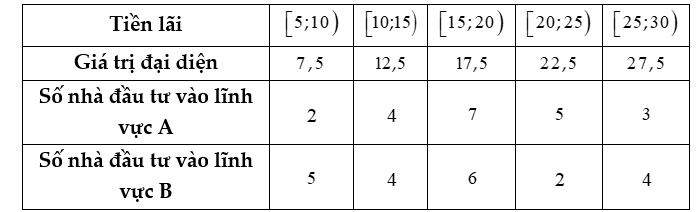
Cho bảng thống kê cân nặng của học sinh (đơn vị: kg) lớp 12D như sau:
|
Nhóm cân nặng |
[30; 40) |
[40; 50) |
[50; 60) |
[60; 70) |
[70; 80) |
[80; 90) |
|
Số học sinh |
2 |
10 |
16 |
8 |
2 |
2 |
Hãy cho biết tính đúng sai của mỗi mệnh đề dưới đây.
a) Số học sinh nặng dưới 50 kilogam là 1. Đúng||Sai
b) Mốt của mẫu số liệu ghép nhóm trên xấp xỉ bằng 54,29(kg). Đúng||Sai
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là . Sai||Đúng
d) Phương sai của mẫu số liệu ghép nhóm là 128. Sai||Đúng
Cho bảng thống kê cân nặng của học sinh (đơn vị: kg) lớp 12D như sau:
|
Nhóm cân nặng |
[30; 40) |
[40; 50) |
[50; 60) |
[60; 70) |
[70; 80) |
[80; 90) |
|
Số học sinh |
2 |
10 |
16 |
8 |
2 |
2 |
Hãy cho biết tính đúng sai của mỗi mệnh đề dưới đây.
a) Số học sinh nặng dưới 50 kilogam là 1. Đúng||Sai
b) Mốt của mẫu số liệu ghép nhóm trên xấp xỉ bằng 54,29(kg). Đúng||Sai
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là . Sai||Đúng
d) Phương sai của mẫu số liệu ghép nhóm là 128. Sai||Đúng
a) Đúng: Số học sinh nặng dưới 50 kg là .
b) Đúng: Nhóm chứa mốt của mẫu số liệu là .
Do đó .
Mốt của mẫu số liệu ghép nhóm xấp xỉ bằng:
Mốt của mẫu số liệu ghép nhóm trên xấp xỉ bằng .
c) Sai: Cỡ mẫu .
Gọi
;
Tứ phân vị thứ nhất của mẫu số liệu gốc là .
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
.
Tứ phân vị thứ ba của mẫu số liệu gốc là .
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
.
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là
d) Sai: Ta có bảng cân nặng của các em học sinh theo giá trị đại diện:
|
Nhóm |
Giá trị đại diện |
Tần số |
| [30; 40) |
35 |
2 |
| [40; 50) |
45 |
10 |
| [50; 60) |
55 |
16 |
| [60; 70) |
65 |
8 |
| [70; 80) |
75 |
2 |
| [80; 90) |
85 |
2 |
Cỡ mẫu .
Số trung bình của mẫu số liệu ghép nhóm là
Phương sai của mẫu số liệu ghép nhóm là
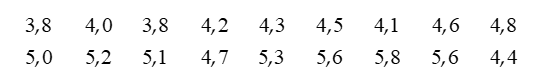






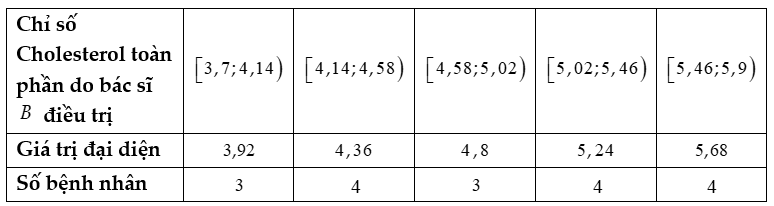
 Số trung bình của mẫu số liệu trên do bác sĩ
Số trung bình của mẫu số liệu trên do bác sĩ