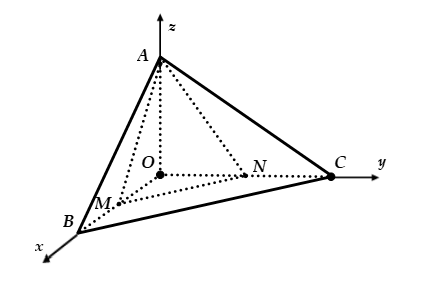
Trong không gian , cho điểm
. Mặt phẳng
đi qua
cắt các trục
,
lần lượt tại
khác gốc tọa độ sao cho
đạt giá trị nhỏ nhất, trong đó
lần lượt là diện tích các tam giác
và
lần lượt là diện tích các tam giác
. Điểm
nào dưới đây thuộc
?
Ta có . Lại có
,
và
.
Đặt , ta có
Tương tự, ta có và
.
Khi đó .
Dấu "=" xảy ra khi và chỉ khi hay
.
Từ đó suy ra nhận
làm vectơ pháp tuyến.
Do đó có phương trình
.
Vậy là điểm thuộc
.