Cho tứ diện và các điểm
xác định bởi
. Tìm
để các đường thẳng
cùng song song với một mặt phẳng?
Cho tứ diện và các điểm
xác định bởi
. Tìm
để các đường thẳng
cùng song song với một mặt phẳng?
Cho tứ diện và các điểm
xác định bởi
. Tìm
để các đường thẳng
cùng song song với một mặt phẳng?
Cho tứ diện và các điểm
xác định bởi
. Tìm
để các đường thẳng
cùng song song với một mặt phẳng?
Cho tứ diện có
đôi một vuông góc.
là một điểm bất kì thuộc miền trong tam giác
. Tìm giá trị nhỏ nhất của biểu thức
?
Đặt . Khi đó
với
là ba số có tổng bằng 1.
Ta có:
Tương tự ta được
Do đó
Ta biết rằng H là chân đường cao kẻ từ đỉnh O của tứ diện vuông OABC khi và chỉ khi H là trực tâm của tam giác ABC. Hơn nữa
Do đó
Dấu "=" xảy ra khi và chỉ khi OM = OH hay M trùng H.
Vậy min T = 2, đạt được khi M trùng H hay M là trực tâm của tam giác ABC.
Một chiếc cần cẩu, cẩu tấm kim loại có trọng lực , được thiết kế với tấm kim loại được giữ bởi ba đoạn cáp
sao cho
và
là tam giác đều, đồng thời các cạnh
tạo với mặt phẳng
một góc có
(như hình vẽ).
Tìm độ lớn của lực căng của mỗi sợi dây cáp? (Kết quả làm tròn đến hàng đơn vị)
Đáp án: 1333(N)
Một chiếc cần cẩu, cẩu tấm kim loại có trọng lực , được thiết kế với tấm kim loại được giữ bởi ba đoạn cáp
sao cho
và
là tam giác đều, đồng thời các cạnh
tạo với mặt phẳng
một góc có
(như hình vẽ).
Tìm độ lớn của lực căng của mỗi sợi dây cáp? (Kết quả làm tròn đến hàng đơn vị)
Đáp án: 1333(N)
Đặt thì
.
Chú ý thêm là:
Ta có:
với
là trọng tâm
.
Vì hình chóp đều nên
Do đó , suy ra
.
Khi gắn các lực vào ta có:
Từ đó: .
Vậy lực căng mỗi sợi dây là .
Cho tứ diện ,
là một điểm nằm trong tứ diện. Các đường thẳng
cắt các mặt
lần lượt tại
. Mặt phẳng
đi qua
và song song với
lần lượt cắt
tại các điểm
.Khẳng định nào sau đây là đúng nhất. Chứng minh
là trọng tâm của tam giác
.
Hình vẽ minh họa
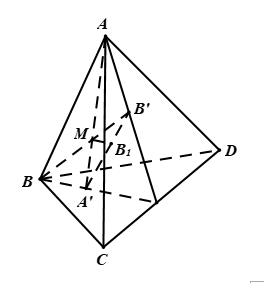
Vì nằm trong tứ diện
nên
tồn tại sao cho
Gọi là mặt phẳng đi qua
và song song với mặt phẳng
.
Ta có .
Do đó
Trong , chiếu các vec tơ lên đường thẳng
theo phương
ta được:
Từ suy ra
Tương tự ta có
Mặt khác chiếu các vec tơ trong lên mặt phẳng
theo phương
tì thu được
.
Vậy từ ta có
, hay
là trọng tâm của tam giác
.
Cho tứ diện có
và
. Gọi
và
lần lượt là trung điểm của
và
. Hãy xác định góc giữa cặp vectơ
và
?
Hình vẽ minh họa
Xét tam giác có
là trung điểm đoạn
.
Ta có:
Vì tam giác có
và
Nên tam giác đều. Suy ra:
Tương tự ta có tam giác đều nên
.
Xét .
Suy ra . Hay góc giữa cặp vectơ
và
bằng
.
Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?
Nếu thì
Suy ra tứ giác là hình bình hành
Mệnh đề sai vì:
Cho lập phương có cạnh bằng
. Gọi
là trọng tâm tam giác
. Khẳng định nào sau đây đúng?
Hình vẽ minh họa
Ta có:
Do G là trọng tâm tam giác suy ra
Cho tứ diện . Gọi
lần lượt là trung điểm của
. Đặt
. Khẳng định nào sau đây đúng?
Ta có:
Vậy khẳng định đúng .
Gọi lần lượt là trung điểm của các cạnh
và
của tứ diện
. Gọi
là trung điểm đoạn
và
là 1 điểm bất kỳ trong không gian. Tìm giá trị của
thích hợp điền vào đẳng thức vectơ:
.
Ta có ,
nên
Vậy
Cho hình chóp có
,
. Gọi
là mặt phẳng đi qua
và các trung điểm của
. Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng
.
Hinh vẽ minh họa
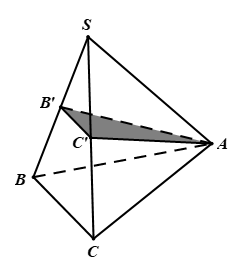
Gọi lần lượt là trung điểm của
. Thiết diện là tam giác
.
Theo bài tập 5 thì
Ta có
.
Tính tương tự, ta có
.
Vậy
.
Trong không gian , cho các điểm
,
, điểm
và tam giác
vuông tại
, hình chiếu vuông góc của
trên
là điểm
. Khi đó điểm
luôn thuộc đường tròn cố định có bán kính bằng
Hình vẽ minh họa
Dễ thấy . Ta có
và
, suy ra
.
Ta có
, mà
. Suy ra
.
Mặt khác ta có
, .
Từ và
suy ra
và
.
Với suy ra
thuộc mặt phẳng
với
là mặt phẳng đi qua O và vuông góc với đường thẳng
.
Phương trình của là:
.
Với
vuông tại
.
Do đó thuộc mặt cầu
có tâm
là trung điểm của
và bán kính
.
Do đó điểm luôn thuộc đường tròn
cố định là giao tuyến của mp
với mặt cầu
.
Giả sử có tâm
và bán kính
thì
và
.
Vậy điểm luôn thuộc đường tròn cố định có bán kính bằng
.
Cho hình hộp . Chọn khẳng định đúng?
Hình vẽ minh họa
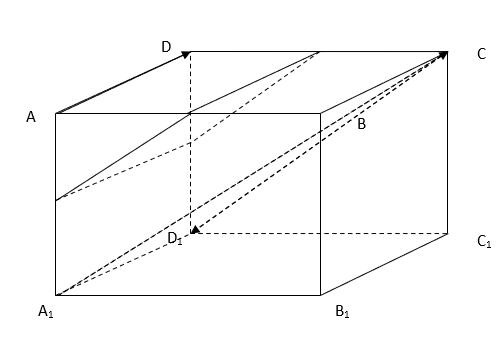
lần lượt là trung điểm của
.
Ta có
đồng phẳng.
Gọi lần lượt là trung điểm của các cạnh
của tứ diện
. Gọi
là trung điểm của đoạn
. Tìm giá trị thực của
thỏa mãn đẳng thức vectơ
?
Gọi lần lượt là trung điểm của các cạnh
của tứ diện
. Gọi
là trung điểm của đoạn
. Tìm giá trị thực của
thỏa mãn đẳng thức vectơ
?
Cho hình chóp có
, các cạnh
đôi một vuông góc. Gọi
là trung điểm của
. Tính tích vô hướng của hai vectơ
.
Hình vẽ minh họa
Ta có:
Vậy
Cho tứ diện . Gọi
và
lần lượt là trung điểm của
và
Tìm giá trị của
thích hợp điền vào đẳng thức vectơ:
Ta có:
Mà và
lần lượt là trung điểm của
và
nên
Do đó .
Cho hình chóp có
. Một mặt phẳng
luôn đi qua trọng tâm của tam giác
, cắt các cạnh
lần lượt tại
. Tìm giá trị nhỏ nhất của
.
Gọi là trọng tâm của tam giác
. Ta có
.
Mà đồng phẳng nên
Theo BĐT Cauchy schwarz:
Ta có
.
Đẳng thức xảy ra khi
kết hợp với
ta được;
.
Vậy GTNN của là
.
Cho tam giác , thì công thức tính diện tích nào sau đây là đúng nhất.
Ta có:
.
Cho tứ diện . Gọi
theo thứ tự là trung điểm
và
. Khẳng định nào sau đây đúng?
Xác định tính đúng sai của các khẳng định sau:
a) Sai||Đúng
b) Đúng||Sai
c) Sai||Đúng
d) Đúng||Sai
Cho tứ diện . Gọi
theo thứ tự là trung điểm
và
. Khẳng định nào sau đây đúng?
Xác định tính đúng sai của các khẳng định sau:
a) Sai||Đúng
b) Đúng||Sai
c) Sai||Đúng
d) Đúng||Sai
a) Vì là trung điểm của
và
nên
và
Nên .
b) Ta có:
c) Ta có:
d) Do N là trung điểm của CD nên
Cho hình chóp có đáy
là hình bình hành tâm
. Điểm
là điểm thỏa mãn
. Khẳng định nào sau đây đúng?
Hình vẽ minh họa
Gọi O là tâm hình bình hành suy ra
Ta có:
suy ra ba điểm
thẳng hàng.
Cho tam giác vuông tại
và có hai đỉnh
nằm trên mặt phẳng
. Gọi
là hình chiếu vuông góc của đỉnh
lên
. Trong các mệnh đề sau, mệnh đề nào đúng?
Nếu A nằm trên (P) tức A’ trùng với A thì tam giác A’BC có góc A vuông, nếu A không nằm trên (P) thì
suy ra góc
là góc tù.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

