VnDoc.com Lớp 12 Trắc nghiệm Toán 12 Kết nối tri thức

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Bài tập trắc nghiệm Toán 12 KNTT Bài 10 (Mức độ Dễ)

Nhận biết Thông hiểu Vận dụng Vận dụng cao

Bài kiểm tra này bao gồm 20 câu
Điểm số bài kiểm tra: 20 điểm
Xem lại kỹ lý thuyết trước khi làm bài
Chuẩn bị giấy và bút để nháp trước khi bắt đầu

Bắt đầu!!

00:00:00

Câu 1: Thông hiểu

Tính độ lệch chuẩn của mẫu số liệu

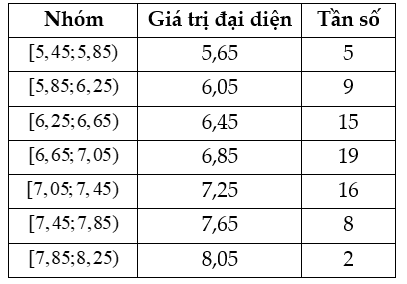
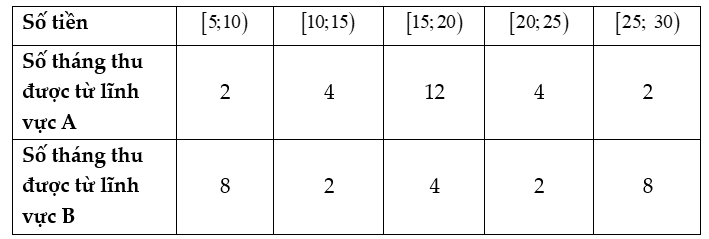
Cho bảng số liệu thống kê cân nặng của 50 học sinh tiểu học như sau:

Cân nặng (kg)	Số học sinh
[0; 10)	5
[10; 20)	8
[20; 60)	15
[30; 80)	16
[40; 100)	6

Tìm độ lệch chuẩn của mẫu số liệu đã cho?

A.
$12,2$
B.
$11,5$
C.
$9,8$
D.
$10,8$

Hướng dẫn:

Ta có:

Cân nặng (kg)	Số học sinh	Giá trị đại diện (x_i)	$\left( x_{i} - \overline{x} ight)^{2}$	$f_{i}.\left( x_{i} - \overline{x} ight)^{2}$
[0; 10)	5	5	484	2420
[10; 20)	8	15	144	1152
[20; 60)	15	25	4	60
[30; 80)	16	35	64	1024
[40; 100)	6	45	324	1944
	$\sum_{}^{}f_{i} = 50$			Tổng: 6600

Phương sai của mẫu số liệu là:

$S^{2} = \frac{1}{N}.\sum_{}^{}{f_{i}.\left( x_{i} - \overline{x} ight)^{2}} = \frac{1}{50}.6600 = 132$

Suy ra độ lệch chuẩn của mẫu số liệu là: $S = \sqrt{S^{2}} = \sqrt{132} \approx 11,5$

Câu 2: Nhận biết

Tính điểm trung bình của từng lớp

Kết quả thống kê điểm trung bình năm học của hai lớp 12C và 12D như sau:

Điểm trung bình	[5; 6)	[6; 7)	[7; 8)	[8; 9)	[9; 10)
Số học sinh lớp 12C	4	5	3	4	2
Số học sinh lớp 12CD	2	5	4	3	1

Điểm trung bình của lớp 12C và điểm trung bình của lớp 12D lần lượt là:

A.
$\frac{65}{9};\frac{217}{30}$
B.
$\frac{42}{5};\frac{37}{3}$
C.
$\frac{217}{30};\frac{65}{9}$
D.
$\frac{37}{3};\frac{42}{5}$

Hướng dẫn:

Ta có:

Điểm trung bình	[5; 6)	[6; 7)	[7; 8)	[8; 9)	[9; 10)
Giá trị đại diện	5,5	6,5	7,5	8,5	9,5
Số học sinh lớp 12C	4	5	3	4	2
Số học sinh lớp 12CD	2	5	4	3	1

Điểm trung bình của lớp 12C:

$\overline{x_{C}} = \frac{4.5,5 + 5.6,5 + 3.7,5 + 4.8,5 + 2.9,5}{18} = \frac{65}{9}$ .

Điểm trung bình của lớp 12D:

$\overline{x_{D}} = \frac{2.5,5 + 5.6,5 + 4.7,5 + 3.8,5 + 1.9,5}{15} = \frac{217}{30}$ .

Câu 3: Thông hiểu
Tìm phương sai của mẫu số liệu ghép nhóm
Một mẫu số liệu có bảng tần số ghép nhóm như sau:

Nhóm
$\lbrack 1;5)$ $\lbrack 5;9)$ $\lbrack 9;13)$ $\lbrack 13;17)$ $\lbrack 17;21)$

Tần số
$4$ $8$ $13$ $6$ $4$

Phương sai của mẫu số liệu là (kết quả làm tròn đến hàng phần trăm)
- A.
  $23$ .
- B.
  $21,01$ .
- C.
  $20,01$ .
- D.
  $22$ .
Hướng dẫn:
Xét mẫu số liệu ghép nhóm cho bởi bảng sau

Nhóm
$\lbrack 1;5)$ $\lbrack 5;9)$ $\lbrack 9;13)$ $\lbrack 13;17)$ $\lbrack 17;21)$

Giá trị đại diện

3

7

11

15

19

Tần số
$4$ $8$ $13$ $6$ $4$

Số trung bình của mẫu số liệu là:

$\overline{x} = \frac{1}{35}.(3.4 + 7.8 + 11.13 + 15.6 + 19.4) \approx 10,77$

Phương sai của mẫu số liệu ghép nhóm là

$S^{2} = \frac{1}{35}\left( 4.3^{2} + 8.7^{2} + 13.11^{2} + 6.15^{2} + 4.19^{2} \right) - 10,77^{2} \approx 21,01$
Câu 4: Thông hiểu
Tính độ lệch chuẩn
Một siêu thị thống kê số tiền (đơn vị: chục nghìn đồng) mà 44 khách hàng mua hàng ở siêu thị đó trong một ngày. Số liệu được ghi lại trong bảng sau:

Nhóm

Tần số

[40; 45)

4

[45; 50)

14

[50; 55)

8

[55; 60)

10

[60; 65)

6

[65; 70)

2

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là:
- A.
  $7,3$
- B.
  $6,8$
- C.
  $46,1$
- D.
  $3,3$
Hướng dẫn:
Ta có:

Nhóm

Giá trị đại diện

Tần số

[40; 45)

42,5

4

[45; 50)

47,5

14

[50; 55)

52,5

8

[55; 60)

57,5

10

[60; 65)

62,5

6

[65; 70)

67,5

2

Số trung bình cộng của mẫu số liệu ghép nhóm là:

$\overline{x} = \frac{4.42,5 + 14.47,5 + 8.52,5 + 10.57,6 + 6.62,5 + 2.67,5}{44} = \frac{585}{11}$

Phương sai của mẫu số liệu ghép nhóm là:

$s^{2} = \lbrack 4.\left( 42,5 - \frac{585}{11} ight)^{2} + 14.\left( 47,5 - \frac{585}{11} ight)^{2} + 8.\left( 52,5 - \frac{585}{11} ight)^{2}$

$+ 10.\left( 57,6 - \frac{585}{11} ight)^{2} + 6.\left( 62,5 - \frac{585}{11} ight)^{2} + 2.\left( 67,5 - \frac{585}{11} ight)^{2}brack:44 \approx 46,12$

Vậy độ lệch chuẩn của mẫu số liệu ghép nhóm là:

$s = \sqrt{s^{2}} = \sqrt{46,12} \approx 6,8$
Câu 5: Nhận biết
Chọn kết luận đúng
Số đặc trưng nào không sử dụng thông tin của nhóm số liệu đầu tiên và nhóm số liệu cuối cùng?
- A.
  Khoảng biến thiên.
- B.
  Độ lệch chuẩn.
- C.
  Phương sai.
- D.
  Khoảng tứ phân vị.
Hướng dẫn:
Theo các công thức tính khoảng biến thiên, khoảng tứ phân vị, phương sai, độ lệch chuẩn ta thấy khoảng tứ phân vị là không sử dụng thông tin của nhóm số liệu đầu và nhóm số liệu cuối.
Câu 6: Nhận biết
Chọn đáp án đúng
Cho mẫu số liệu ghép nhóm với bộ ba tứ phân vị lần lượt là $Q_{1} = 11,5$ ; $Q_{2} = 14,5$ ; $Q_{3} = 21,3.$ Khi đó khoảng tứ phân vị của mẫu số liệu trên là
- A.
  $\Delta Q = 6,8$ .
- B.
  $\Delta Q = 3,0$ .
- C.
  $\Delta Q = 32,8$ .
- D.
  $\Delta Q = 9,8$ .
Hướng dẫn:
Khoảng tứ phân vị của mẫu số liệu là: $\Delta Q = Q_{3} - Q_{1} = 21,3 - 11,5 = 9,8$ .
Câu 7: Nhận biết
Chọn kết luận đúng
Một mẫu số liệu ghép nhóm có phương sai bằng 25 thì có độ lệch chuẩn bằng
- A.
  $50.$
- B.
  $4.$
- C.
  $5.$
- D.
  $256.$
Hướng dẫn:
Ta có độ lệch chuẩn bằng căn bậc hai số học của phương sai nên $s = 5.$
Câu 8: Nhận biết

Xét tính đúng sai của các nhận định

Một nhà thực vật học độ chiều dài trung bình của 74 lá cây (đơn vị: milimét) và thu được bảng tần số ghép nhóm như sau:

a) Chiều dài trung bình của 74 lá cây bằng $\approx 6,4(\ mm)$ . Sai||Đúng

b) Khoảng biến thiên của mẫu số liệu là $2,4$ . Sai||Đúng

c) Phương sai của mẫu số liệu $\approx 0,35$ . Đúng||Sai

d) Khoảng tứ phân vị của mẫu số liệu trên $\approx 8,93$ . Sai||Đúng

(Các kết quả tính được trong bài làm tròn đến hàng phần trăm)

Đáp án là:

Một nhà thực vật học độ chiều dài trung bình của 74 lá cây (đơn vị: milimét) và thu được bảng tần số ghép nhóm như sau:

a) Chiều dài trung bình của 74 lá cây bằng $\approx 6,4(\ mm)$ . Sai||Đúng

b) Khoảng biến thiên của mẫu số liệu là $2,4$ . Sai||Đúng

c) Phương sai của mẫu số liệu $\approx 0,35$ . Đúng||Sai

d) Khoảng tứ phân vị của mẫu số liệu trên $\approx 8,93$ . Sai||Đúng

(Các kết quả tính được trong bài làm tròn đến hàng phần trăm)

a) Chiều dài trung bình của 74 lá cây là:

$\overline{x} = \frac{1}{74}.\lbrack 5,65.5 + 6,05.9 + 6,45 \cdot 15 + 6,85 \cdot 19 + 7,25.16 + 7,65 \cdot 8 + 8,05.2\rbrack$

$= \frac{5029}{740} \approx 6,8(\ mm)$

Suy ra a) sai.

b) Khoảng biến thiên của mẫu số liệu là $8,25 - 5,45 = 2,8$ nên b) sai.

c) Phương sai của mẫu số liệu trên là

${S_{x}}^{2} = \frac{5.(5,65 - 6,8)^{2} + 9.(6,05 - 6,8)^{2} + 15.(6,45 - 6,8)^{2}}{74}$

$+ \frac{19.(6,85 - 6,8)^2+ 16.(7,25 -6,8)^{2}}{74}$

$+ \frac{8(7,65 - 6,8)^{2} + 2(8,05 - 6,8)^{2}}{74} \approx 0,35(\ mm)$

Vậy c) đúng.

d) Cỡ mẫu: $n = 5 + 9 + 15 + 19 + 16 + 8 + 2 = 74$ .

Gọi $x_{1};\ x_{2};\ \ldots;\ x_{74}$ là độ dài của 74 lá cây và được sắp xếp theo thứ tự không giảm.

Tứ phân vị thứ nhất $Q_{1}$ là $x_{19}$ . Do $x_{19}$ thuộc nhóm $\lbrack 6,25;6,65)$ nên ta có $Q_{1} = 6,25 + \frac{\frac{74}{4} - 14}{15}.4 = 7,45$ .

Tứ phân vị thứ ba $Q_{3}$ là $x_{56}$ . Do $x_{56}$ thuộc nhóm $\lbrack 7,05;7,45)$ nên ta có $Q_{3} = 7,05 + \frac{\frac{3.74}{4} - 48}{16}.4 \approx 8,93$ .

Khi đó khoảng tứ phân vị là $\Delta_{Q} = Q_{3} - Q_{1} \approx 1,48$ . Vậy d) sai.
Câu 9: Nhận biết

Xét tính đúng sai của các nhận định

Số tiền đầu tư của một cửa hàng đối với hai lĩnh vực A, B là như nhau và số tiền thu được mỗi tháng trong 24 tháng từ hai lĩnh vực trên được ghi lại ở bảng sau (đơn vị: triệu đồng):

a) Giá trị trung bình khi đầu tư vào 2 lĩnh vực A và B là như nhau. Đúng||Sai

b) Phương sai của số tiền thu được từ lĩnh vực A qua các tháng là 5.Sai||Đúng

c) Độ lệch chuẩn của số tiền thu được từ lĩnh vực B qua các tháng $\approx 8, 42$ . Đúng||Sai

d) Đầu tư vào lĩnh vực B rủi ro hơn. Đúng||Sai

Đáp án là:

Số tiền đầu tư của một cửa hàng đối với hai lĩnh vực A, B là như nhau và số tiền thu được mỗi tháng trong 24 tháng từ hai lĩnh vực trên được ghi lại ở bảng sau (đơn vị: triệu đồng):

a) Giá trị trung bình khi đầu tư vào 2 lĩnh vực A và B là như nhau. Đúng||Sai

b) Phương sai của số tiền thu được từ lĩnh vực A qua các tháng là 5.Sai||Đúng

c) Độ lệch chuẩn của số tiền thu được từ lĩnh vực B qua các tháng $\approx 8, 42$ . Đúng||Sai

d) Đầu tư vào lĩnh vực B rủi ro hơn. Đúng||Sai

Số tiền trung bình thu được từ lĩnh vực A, B tương ứng là

$\overline{x_{A}} = \frac{1}{24}(2.7,5 + 4.12,5 + 12.17,5 + 4.22,5 + 2.27,5) = 17,5$

$\overline{x_{B}} = \frac{1}{24}(8.7,5 + 2.12,5 + 4.17,5 + 2.22,5 + 8.27,5) = 17,5$

Suy ra a) đúng.

Phương sai của số tiền thu được hàng tháng khi đầu tư vào lĩnh vực A, B tương ứng là:

$S_{\ _{x_{A}}}^{2} = \frac{1}{24}\lbrack 2.(17,5 - 7,5)^{2} + 4.(17,5 - 12,5)^{2}$

$+ 12.0^{2} + 4.(17,5 - 22,5)^{2} + 2.(17,5 - 27,5)^{2}\rbrack = 25$

$\Rightarrow S_{x_{A}} = 5$ suy ra b) sai.

$S_{\ _{x_{B}}}^{2} = \frac{1}{24}\lbrack 8.(17,5 - 7,5)^{2} + 2.(17,5 - 12,5)^{2}$

$+ 4.0^{2} + 2.(17,5 - 22,5)^{2} + 8.(17,5 - 27,5)^{2}\rbrack \approx 70,8$

$\Rightarrow S_{x_{B}} \approx 8,42$ suy ra c) đúng.

Do $S_{x_{A}} < S_{x_{B}}$ nên đầu tư vào lĩnh vực B rủi ro nhiều hơn. Suy ra d) đúng.
Câu 10: Nhận biết
Tính chiều cao trung bình
Kết quả đo chiều cao của 50 cây keo trong vườn được thống kê lại trong bảng sau:

Chiều cao (cm)

[120; 122)

[122; 124)

[124; 126)

[126; 128)

[128; 130)

Số cây

16

4

3

6

21

Tính chiều cao trung bình của 50 cây keo trên?
- A.
  $125,89$
- B.
  $125,28$
- C.
  $126,13$
- D.
  $126,47$
Hướng dẫn:
Cỡ mẫu $N = 50$

Chiều cao (cm)

[120; 122)

[122; 124)

[124; 126)

[126; 128)

[128; 130)

Giá trị đại diện

121

123

125

127

129

Số cây

16

4

3

6

21

Chiều cao trung bình là:

$\overline{x} = \frac{16.121 + 4.123 + 3.125 + 6.127 + 21.129}{50} = 125,28$ .
Câu 11: Nhận biết
Chọn đáp án thích hợp
Điểm trung bình cuối năm của học sinh lớp 12A và 12B được thống kê trong bảng sau:

Nếu so sánh bảng biến thiên thì học sinh lớp nào có điểm trung bình ít phân tán hơn?
- A.
  $12B$
- B.
  $12A$
Hướng dẫn:
Ta có:

Khoảng biến thiên của điểm số học sinh lớp 12A là: 10 – 5 = 5

Khoảng biến thiên của điểm số học sinh lớp 12B là: 10 – 6 = 4

Nếu so sánh theo khoảng biến thiên thì điểm trung bình của các học sinh lớp 12B ít phân tán hơn điểm trung bình của các học sinh lớp 12A.
Câu 12: Nhận biết
Chọn đáp án đúng
Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số loại máy tính xách tay được mô tả như sau:

Có bao nhiêu máy tính có thời gian sử dụng từ 7,2 giờ đến 7,6 giờ?
- A.
  $6$
- B.
  $2$
- C.
  $4$
- D.
  $9$
Hướng dẫn:
Có 6 máy tính có thời gian sử dụng từ 7,2 giờ đến 7,6 giờ.
Câu 13: Nhận biết

Xét tính đúng sai của các nhận định

Phỏng vấn một số học sinh lớp $11$ về thời gian (giờ) ngủ của một buổi tối, thu được bảng số liệu sau:

a) Số lượng học sinh nam là 45 bạn. Đúng||Sai

b) Thời gian ngủ trung bình của các bạn học sinh nam là 8 giờ. Đúng||Sai

c) Phương sai của mẫu số liệu trên là $s^{2} = 3$ . Sai||Đúng

d) Độ lệch chuẩn là 9. Sai||Đúng

Đáp án là:

Phỏng vấn một số học sinh lớp $11$ về thời gian (giờ) ngủ của một buổi tối, thu được bảng số liệu sau:

a) Số lượng học sinh nam là 45 bạn. Đúng||Sai

b) Thời gian ngủ trung bình của các bạn học sinh nam là 8 giờ. Đúng||Sai

c) Phương sai của mẫu số liệu trên là $s^{2} = 3$ . Sai||Đúng

d) Độ lệch chuẩn là 9. Sai||Đúng

a) Đúng, b) Đúng, c) Sai, d) Sai.

Số lượng học sinh nam là : $6 + 10 + 13 + 9 + 7 = 45$

Thời gian ngủ trung bình của các bạn học sinh nam là :

$\overline{x} = \frac{1}{45}.\lbrack 6.4,5 + 10.5,5 + 13.6,5 + 9.7,5 + 7.8,5\rbrack = \frac{587}{90}$

Phương sai của mẫu số liệu trên là

$s^{2} = \frac{1}{45}.[ 6.4,5^{2} +10.5,5^{2} + 13.6,5^{2}$ $+ 9.7,5^{2} + 7.8,5^{2}] - \left(\frac{587}{90} \right)^{2} = 1,5773$

Độ lệch chuẩn là $s = \sqrt{1,5773}$ .
Câu 14: Nhận biết
Tìm khoảng biến thiên
Thống kê tốc độ của các loại xe hơi (đơn vị: km/h) được ghi lại như sau:

42

43,4

43,4

46,5

46,7

46,8

47,5

47,7

48,1

48,4

50,8

51,1

52,7

53,9

54,8

57,6

57,5

59,6

60,3

61,1

Lập bảng tần số ghép nhóm với nhóm đầu [42; 46) và độ dài mỗi nhóm bằng 4. Tìm khoảng biến thiên của mẫu dữ liệu ghép nhóm?
- A.
  $R = 28$
- B.
  $R = 30$
- C.
  $R = 20$
- D.
  $R = 25$
Hướng dẫn:
Ta lập được bảng tần số ghép nhóm như sau:

Tốc độ

[42; 46)

[46; 50)

[50; 54)

[54; 58)

[58; 62)

Số xe

3

7

4

3

3

Vậy khoảng biến thiên của mẫu dữ liệu ghép nhóm là $R = 62 - 42 = 20$ .
Câu 15: Thông hiểu
Xác định nhận xét sai
Bộ phận kiểm tra chất lượng sản phẩm dùng máy để đo (chính xác đến $0,001\ mm$ ) độ dày của một chi tiết máy. Kết quả đo một số sản phẩm được thống kê trong bảng sau:

Nhận xét nào sau đây sai?
- A.
  Độ lệch chuẩn của mẫu lớn hơn $2$ .
- B.
  Độ dày của chi tiết máy không bị sai lệch nhiều.
- C.
  Số trung bình của mẫu số liệu gần bằng với $20,77$ .
- D.
  Cỡ mẫu của mẫu số liệu là 60.
Hướng dẫn:
Ta có cỡ mẫu $n = 60$ .

Số trung bình của mẫu số liệu là

$\overline{x} = \frac{3 \cdot 18,5 + 7 \cdot 19,5 + 23 \cdot 20,5 + 25 \cdot 21,5 + 2 \cdot 22,5}{60} = \frac{623}{30} \approx 20,77.$

Phương sai của mẫu số liệu là

$S^{2} = \frac{1}{60}( 3 \cdot18,5^{2} + 7 \cdot 19,5^{2} + 23 \cdot 20,5^{2}$ $+ 25 \cdot 21,5^{2} + 2\cdot 22,5^{2} ) - \left( \frac{623}{30} \right)^{2} =\frac{179}{225}$ .

Độ lệch chuẩn của mẫu số liệu là $S^{2} = \sqrt{\frac{179}{225}} = \frac{\sqrt{179}}{15} \approx 0,89$ .
Câu 16: Thông hiểu
Tìm độ lệch chuẩn của mẫu số liệu ghép nhóm
Điều tra về số tiền mua sách (đơn vị: nghìn đồng) trong một năm của 50 học sinh trong một trường THPT, người ta có bảng sau:

Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
- A.
  242,29
- B.
  233,98
- C.
  265,34
- D.
  264,12
Hướng dẫn:
Chọn giá trị đại diện cho mẫu số liệu, ta có:

Điểm trung bình là:

$\overline{x} = \frac{29 \cdot 100 + 11 \cdot 300 + 3 \cdot 500 + 4 \cdot 700 + 3 \cdot 900}{50} = 264$ .

Phương sai là:

$S^{2} = \frac{1}{50}\lbrack 29 \cdot (100)^{2} + 11 \cdot (300)^{2} + 3 \cdot (500)^{2}$ $+ 4 \cdot (700)^{2} + 3 \cdot (900)^{2}\rbrack - (264)^{2} = 58704$ .

Độ lệch chuẩn: $S = \sqrt{58704} \approx 242,29$ .
Câu 17: Nhận biết
Chọn phương án đúng
Để so sánh mức độ phân tán của các mẫu số liệu ghép nhóm có cùng số trung bình ta dùng đại lượng nào?
- A.
  Khoảng biến thiên.
- B.
  Độ lệch chuẩn.
- C.
  Khoảng tứ phân vị.
- D.
  Trung vị.
Hướng dẫn:
Để so sánh mức độ phân tán của các mẫu số liệu ghép nhóm có cùng số trung bình ta dùng phương sai và độ lệch chuẩn.
Câu 18: Nhận biết
Chọn đáp án đúng
Một mẫu số liệu ghép nhóm có phương sai bằng $16$ có độ lệch chuẩn bằng:
- A.
  $4$
- B.
  $- 4$
- C.
  $16$
- D.
  $256$
Hướng dẫn:
Mẫu số liệu ghép nhóm có phương sai bằng $16$ có độ lệch chuẩn bằng $\sqrt{16} = 4$ .
Câu 19: Nhận biết

Xét tính đúng sai của các nhậnđịnh

Điểm thi của 32 học sinh trong kì thi Tiếng Anh có bảng ghép nhóm sau đây:

a) Số học sinh có điểm thi thấp hơn 60 là 10. Đúng||Sai

b) Giá trị đại diện của nhóm [70;80) là 75. Đúng||Sai

c) Điểm thi trung bình môn tiếng anh của 32 học sinh bằng 75. Sai||Đúng

d) Độ lệch chuẩn bằng: 100. Sai||Đúng

Đáp án là:

Điểm thi của 32 học sinh trong kì thi Tiếng Anh có bảng ghép nhóm sau đây:

a) Số học sinh có điểm thi thấp hơn 60 là 10. Đúng||Sai

b) Giá trị đại diện của nhóm [70;80) là 75. Đúng||Sai

c) Điểm thi trung bình môn tiếng anh của 32 học sinh bằng 75. Sai||Đúng

d) Độ lệch chuẩn bằng: 100. Sai||Đúng

a) Đúng b) Đúng, c) Sai d) Sai.

Số học sinh có điểm thi thấp hơn 60 là 4 + 6 =10.

Giá trị đại diện của nhóm [70;80) là $\frac{70 + 80}{2} = 75$ .

Điểm thi trung bình môn tiếng anh của 32 học sinh bằng :

$\overline{x} = \frac{1}{32}.\lbrack 4.45 + 6.55 + 10.65 + 6.75 + 4.85 + 2.95\rbrack = 66,875$

Phương sai là:

$s^{2} = \frac{4.(45 - 66,87)^{2} + 6.(55 - 66,87)^{2}}{32}$ $+ \frac{10.(65 - 66,87)^{2} + 6.(75 - 66,87)^{2}}{32}$

$+ \frac{4.(85 - 66,87)^{2} + 2.(95 - 66,87)^{2}}{32} \approx 190,2344$

$s = \sqrt{190,2344}$
Câu 20: Nhận biết

Hoàn thành bảng số liệu

Cho biểu đồ

Hoàn thảnh bảng số liệu theo mẫu sau:

Chiều cao

[160; 164)

[164; 168)

[168; 172)

[172; 176)

[176; 180)

Số học sinh

3

5

8

4

1

Giá trị đại diện

162

166

170

174

178

Đáp án là:

Cho biểu đồ

Hoàn thảnh bảng số liệu theo mẫu sau:

Chiều cao

[160; 164)

[164; 168)

[168; 172)

[172; 176)

[176; 180)

Số học sinh

3

5

8

4

1

Giá trị đại diện

162

166

170

174

178

Hoàn thảnh bảng số liệu như sau:

Chiều cao

[160; 164)

[164; 168)

[168; 172)

[172; 176)

[176; 180)

Số học sinh

3

5

8

4

1

Giá trị đại diện

162

166

170

174

178

0/20

20 câu:

Kiểm tra Kiểm tra lại Tiếp tục Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:

Nhận biết (75%):

2/3
Thông hiểu (25%):

2/3

Thời gian làm bài: 00:00:00
Số câu làm đúng: 0
Số câu làm sai: 0
Điểm số: 0
Điểm thưởng: 0

Làm lại

Chia sẻ bởi:
Bọ Cạp

20 Bài viết đã được lưu

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Số điện thoại này đã được xác thực!

Bạn có thể dùng Sđt này đăng nhập tại đây!

Lỗi gửi SMS, liên hệ Admin

Sắp xếp theo

Xóa Đăng nhập để Gửi

Tìm bài trong mục này

Trắc nghiệm Toán 12 Kết nối tri thức
Trắc nghiệm Toán 12 Chân trời sáng tạo
Trắc nghiệm Toán 12 Cánh diều
Trắc nghiệm Toán 12 Sách cũ

Lớp 12
Trắc nghiệm Toán 12 Kết nối tri thức

Trắc nghiệm Toán 12 Kết nối tri thức

Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Khó)
Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Vừa)
Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Dễ)
Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Vừa)
Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Khó)
Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Dễ)

Xem thêm

Nhóm	$\lbrack 1;5)$	$\lbrack 5;9)$	$\lbrack 9;13)$	$\lbrack 13;17)$	$\lbrack 17;21)$
Tần số	$4$	$8$	$13$	$6$	$4$

Nhóm	Tần số
[40; 45)	4
[45; 50)	14
[50; 55)	8
[55; 60)	10
[60; 65)	6
[65; 70)	2

Chiều cao (cm)	[120; 122)	[122; 124)	[124; 126)	[126; 128)	[128; 130)
Số cây	16	4	3	6	21

42	43,4	43,4	46,5	46,7
46,8	47,5	47,7	48,1	48,4
50,8	51,1	52,7	53,9	54,8
57,6	57,5	59,6	60,3	61,1

Tốc độ	[42; 46)	[46; 50)	[50; 54)	[54; 58)	[58; 62)
Số xe	3	7	4	3	3

Chiều cao	[160; 164)	[164; 168)	[168; 172)	[172; 176)	[176; 180)
Số học sinh	3	5	8	4	1
Giá trị đại diện	162	166	170	174	178

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Bài tập trắc nghiệm Toán 12 KNTT Bài 10 (Mức độ Dễ)

Chúc mừng Bạn đã hoàn thành bài!

Trắc nghiệm Toán 12 Kết nối tri thức

Trắc nghiệm Toán 12 Chân trời sáng tạo

Trắc nghiệm Toán 12 Cánh diều

Trắc nghiệm Toán 12 Sách cũ

Lớp 12

Trắc nghiệm Toán 12 Kết nối tri thức

Trắc nghiệm Toán 12 Kết nối tri thức

Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Khó)

Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Vừa)

Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Dễ)

Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Vừa)

Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Khó)

Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Dễ)