Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ Đang cập nhật

Bài tập trắc nghiệm Toán 12 CTST Bài 2 (Mức độ Khó)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Vận dụng
    Tìm m để bất phương trình có nghiệm

    Giá trị của tham số m để bất phương trình (x - 2 - m)\sqrt{x - 1} \leq m - 4 có nghiệm là:

    Hướng dẫn:

    Đặt t = \sqrt{x - 1};(t \geq 0)

    Khi đó bất phương trình ban đầu trở thành:

    \left( t^{2} - m - 1 ight).t \leq m - 4 \Leftrightarrow m \geq \frac{t^{3} - t + 4}{t + 1}

    Xét hàm số f(t) = \frac{t^{3} - t + 4}{t + 1} trên \lbrack 0; + \infty)

    Ta có: f'(t) = \frac{2t^{3} + 3t^{2} - 5}{(t + 1)^{2}} = \frac{(t - 1)\left( 2t^{2} + 5t + 5 ight)}{(t + 1)^{2}}

    f'(t) = 0 \Leftrightarrow t = 1

    Bảng biến thiên của f(t) = \frac{t^{3} - t + 4}{t + 1};t \in \lbrack 0; + \infty)

    Từ bảng biến thiên suy ra để bất phương trình có nghiệm thì m \geq 2.

  • Câu 2: Vận dụng cao
    Tìm min và max của hàm số

    Cho hai số thực x, y thỏa mãn x \geqslant 0;y \geqslant 0 và x + y = 1. Giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P = \frac{x}{{y + 1}} + \frac{y}{{x + 1}} lần lượt là:

    Hướng dẫn:

    Ta có: 

    P = \frac{x}{{y + 1}} + \frac{y}{{x + 1}} = \frac{{x\left( {x + 1} ight) + y\left( {y + 1} ight)}}{{\left( {x + 1} ight)\left( {y + 1} ight)}} = \frac{{{{\left( {x + y} ight)}^2} - 2xy + 1}}{{xy + x + y + 1}} = \frac{{2 - 2xy}}{{2 + xy}}

    Đặt t = xy ta được P = \frac{{2 - 2t}}{{2 + t}}

    Vì x \geqslant 0;y \geqslant 0 \Rightarrow t \geqslant 0

    Mặt khác 1 = x + y \geqslant 2\sqrt {xy} \Leftrightarrow xy \leqslant \frac{1}{4} \Rightarrow t \leqslant \frac{1}{4}

    Khi đó bài toán trở thành tìm giá trị lớn nhất của hàm số g\left( t ight) = \frac{{2 - 2t}}{{2 + t}} trên \left[ {0;\frac{1}{4}} ight]

    Xét hàm số g\left( t ight) = \frac{{2 - 2t}}{{2 + t}} xác định và liên tục trên \left[ {0;\frac{1}{4}} ight]

    Ta có: g'\left( t ight) = \frac{{ - 6}}{{{{\left( {2 + t} ight)}^2}}} < 0,\forall t \in \left( {0;\frac{1}{4}} ight)

    => Hàm số g(t) nghịch biến trên đoạn \left[ {0;\frac{1}{4}} ight]

    => \left\{ {\begin{array}{*{20}{c}} {\mathop {\min }\limits_{\left[ {0;\frac{1}{4}} ight]} g\left( t ight) = g\left( {\dfrac{1}{4}} ight) = \dfrac{2}{3}} \\ {\mathop {\max }\limits_{\left[ {0;\frac{1}{4}} ight]} g\left( t ight) = g\left( 0 ight) = 1} \end{array}} ight.

  • Câu 3: Vận dụng
    Ghi đáp án vào ô trống

    Cho hàm số f(x) liên tục trên \lbrack - 1;3brack và có đồ thị như hình vẽ:

    Giá trị lớn nhất của hàm số y = g(x) =f\left( 3\left| \cos x ight| - 1 ight) bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho hàm số f(x) liên tục trên \lbrack - 1;3brack và có đồ thị như hình vẽ:

    Giá trị lớn nhất của hàm số y = g(x) =f\left( 3\left| \cos x ight| - 1 ight) bằng bao nhiêu?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 4: Thông hiểu
    Chọn phương án thích hợp

    Giá trị nhỏ nhất của hàm số y = x - 5 + \frac{1}{x} trên khoảng (0; + \infty) bằng bao nhiêu?

    Hướng dẫn:

    Áp dụng bất đẳng thức Cô – si ta có:

    y = x + \frac{1}{x} - 5 \geq 2\sqrt{x.\frac{1}{x}} - 5 = - 3

    Dấu bằng xảy ra khi x = \frac{1}{x} \Leftrightarrow x^{2} = 1 \Leftrightarrow x = 1 (vì x > 0).

    Vậy \min_{(0; + \infty)}y = - 3

  • Câu 5: Vận dụng
    Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

    Cho hàm số f(x) có đạo hàm f’(x). Đồ thị của hàm số y = f’(x) được biểu diễn trong hình vẽ dưới đây.

    Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

    Biết rằng f\left( 0 ight) + f\left( 1 ight) + f\left( 3 ight) = f\left( 4 ight) + 2f\left( 2 ight). Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số f(x) trên đoạn [0; 4]?

    Hướng dẫn:

    Ta có bảng xét dấu như sau:

    Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

    Dựa vào bảng xét dấy ta có M = f(2), GTNN chỉ có thể là f(0) hoặc f(4)

    Ta lại có

    f(1) và f(3) nhỏ hơn f(2) => f(1) + f(3) < 2f(2)

    => 2f(2) – f(1) – f(3) > 0

    Theo bài ra ta có:

    f(0) + f(1) + f(3) = f(4) + 2f(2)

    => f(0) – f(4) = 2f(2) – f(1) – f(3) > 0

    => f(0) – f(4) > 0 => f(0) > f(4)

    => GTNN đạt được tại x = 4

  • Câu 6: Vận dụng
    Ghi đáp án vào ô trống

    Một công ty du lịch tổ chức tour du lịch với giá mỗi tour là 5000000 đồng một khách cho 30 khách. Từ khách thứ 31, cứ thêm một khách, giá của tour lại được giảm a nghìn (a là số nguyên dương). Số khách thêm của tour không quá 15 người. Biết rằng nếu nhận thêm từ 1 đến 8 khách thì doanh thu tăng dần theo số khách nhận thêm. Tìm giá trị lớn nhất của a.

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Một công ty du lịch tổ chức tour du lịch với giá mỗi tour là 5000000 đồng một khách cho 30 khách. Từ khách thứ 31, cứ thêm một khách, giá của tour lại được giảm a nghìn (a là số nguyên dương). Số khách thêm của tour không quá 15 người. Biết rằng nếu nhận thêm từ 1 đến 8 khách thì doanh thu tăng dần theo số khách nhận thêm. Tìm giá trị lớn nhất của a.

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 7: Vận dụng
    Tính tỉ số giữa a và r

    Một sợi dây kim loại dài 60cm được cắt thành hai đoạn. Đoạn dây thứ nhất uốn thành hình vuông cạnh a, đoạn dây thứ hai uốn thành đường tròn bán kính r.

    Để tổng diện tích của hình vuông và hình tròn nhỏ nhất thì tỉ số \frac{a}{r} bằng:

    Hướng dẫn:

    Gọi x (cm) là độ dài của đoạn dây cuộn thành hình tròn (0 < x < 60) \Rightarrow Chiều dài đoạn còn lại là 60 - x (cm).

    Chu vi đường tròn 2\pi r = x \Rightarrow r = \frac{x}{2\pi} \rightarrow diện tích hình tròn S_{1} = \pi.r^{2} = \frac{x^{2}}{4\pi}

    Diện tích hình vuông cạnh a = \frac{60 - x}{4} là S_{2} = \left( \frac{60 - x}{4} \right)^{2}.

    Tổng diện tích hai hình:

    S = S_{1} + S_{2} = \frac{x^{2}}{4\pi} + \left( \frac{60 - x}{4} \right)^{2} = \frac{(4 + \pi).x^{2} - 120\pi x + 3\ \ 600\pi}{16\pi} .

    Đạo hàm S' = \frac{(4 + \pi).x - 60\pi}{8\pi};\ \ \ S' = 0 \Leftrightarrow x = \frac{60\pi}{4 + \pi};\ \ \ S'' = \frac{4 + \pi}{8\pi} > 0.

    Suy ra hàm S chỉ có một điểm cực tiểu là x = \frac{60\pi}{4 + \pi}.

    Do đó S đạt giá trị nhỏ nhất tại x = \frac{60\pi}{4 + \pi}.

    Với x = \frac{60\pi}{4 + \pi} \Rightarrow r = \frac{30}{4 + \pi} và a = \frac{60}{4 + \pi} \Rightarrow \frac{a}{r} = 2.

  • Câu 8: Vận dụng cao
    Tìm liều lượng thuốc lớn nhất cần dùng

    Độ giảm huyết áp của một bệnh nhân được cho bởi công thức G\left( x ight) = 0,035{x^2}.\left( {15 - x} ight), trong đó x là liều lượng thuốc được tiêm cho bệnh nhân (x được tính bằng miligam). Tính liều lượng thuốc cần tiêm (đơn vị miligam) cho bệnh nhân để huyết áp giảm nhiều nhất.

    Hướng dẫn:

    Xét G\left( x ight) = 0,035{x^2}.\left( {15 - x} ight) ta có:

    \begin{matrix} G'\left( x ight) = 0,035\left( {30x - 3{x^2}} ight) \hfill \\ G'\left( x ight) = 0 \Rightarrow \left[ {\begin{array}{*{20}{c}} {x = 0} \\ {x = 10} \end{array}} ight. \hfill \\ \end{matrix}

    Mặt khác \left\{ {\begin{array}{*{20}{c}} {G\left( 0 ight) = G\left( {15} ight) = 0} \\ {G\left( {10} ight) = 17,5} \end{array}} ight. \Rightarrow \mathop {\max }\limits_{\left[ {0;15} ight]} = 17,5 \Rightarrow x = 10

  • Câu 9: Vận dụng cao
    Xét tính đúng sai của các nhậnđịnh

    Một tấm bìa cứng hình chữ nhật có kích thước 3m \times 8m. Người ta cắt mỗi góc của tấm bìa một hình vuông có cạnh là x để tạo ra hình hộp chữ nhật không nắp. Xét tính đúng, sai của các mệnh đề sau:

    a) Điều kiện của x là 0 < x < \frac{3}{2}. Đúng||Sai

    b) Diện tích mặt đáy của chiếc hộp là (8 - 2x)(3 - 2x). Đúng||Sai

    c) Thể tích của chiếc hộp là (8 - 2x)^{2}(3 - 2x). Sai||Đúng

    d) Với x = \frac{2}{3}(m) thì chiếc hộp có thể tích lớn nhất. Đúng||Sai

    Đáp án là:

    Một tấm bìa cứng hình chữ nhật có kích thước 3m \times 8m. Người ta cắt mỗi góc của tấm bìa một hình vuông có cạnh là x để tạo ra hình hộp chữ nhật không nắp. Xét tính đúng, sai của các mệnh đề sau:

    a) Điều kiện của x là 0 < x < \frac{3}{2}. Đúng||Sai

    b) Diện tích mặt đáy của chiếc hộp là (8 - 2x)(3 - 2x). Đúng||Sai

    c) Thể tích của chiếc hộp là (8 - 2x)^{2}(3 - 2x). Sai||Đúng

    d) Với x = \frac{2}{3}(m) thì chiếc hộp có thể tích lớn nhất. Đúng||Sai

    Hình vẽ minh họa

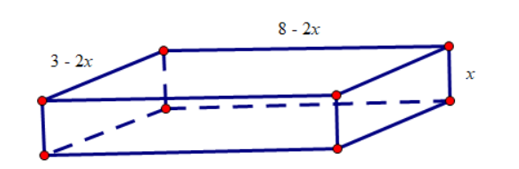
    a) Ta có chiều dài, chiều rộng, chiều cao của chiếc hộp lần lượt là 8 - 2x;3 - 2x;\ x.

    Suy ra điều kiện của x là 0 < x < \frac{3}{2}. Vậy a) Đúng.

    b) Đáy của chiếc hộp là hình chữ nhật có diện tích là S = (8 - 2x)(3 - 2x). Vậy b) Đúng.

    c) Thể tích của chiếc hộp là: V = x(8 - 2x)(3 - 2x). Vậy c) Sai.

    d) Xét hàm số: V(x) = x(3 - 2x)(8 - 2x) = 4x^{3} - 22x^{2} + 24x trên \left( 0;\frac{3}{2} \right).

    Ta có: V'(x) = 12x^{2} - 44x + 24 = 4\left( 3x^{2} - 11x + 6 \right).

    Khi đó: V'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 3 \\ x = \frac{2}{3} \end{matrix} \right..

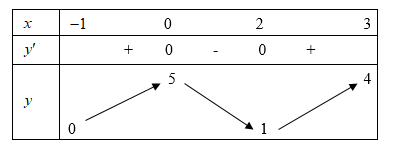
    Bảng biến thiên:

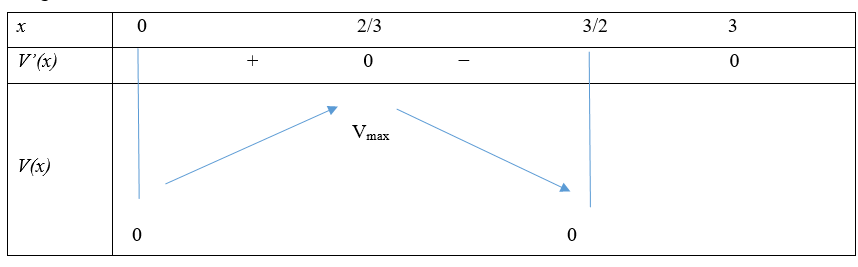
    Từ BBT ta thấy hàm số đạt giá trị lớn nhất trên \left( 0;\frac{3}{2} \right) khi x = \frac{2}{3}. Vậy d) Đúng

  • Câu 10: Vận dụng
    Tìm các giá trị nguyên của tham số m

    Có bao nhiêu giá trị nguyên của tham số m để giá trị lớn nhất của hàm số y = \frac{m\sin x + 1}{\cos x + 2} nhỏ hơn 2?

    Hướng dẫn:

    Ta có: y = \frac{m\sin x + 1}{\cos x + 2}\Leftrightarrow m\sin x + 1 = y\cos x + 2y

    \Leftrightarrow m\sin x - y\cos x = 2y - 1

    Phương trình có nghiệm khi

    m^{2} + y^{2} \geq (2y - 1)^{2} \Leftrightarrow m^{2} + y^{2} \geq 4y^{2} - 4y + 1

    \Leftrightarrow 3y^{2} - 4y + 1 - m^{2} \leq 0

    Xét phương trình 3y^{2} - 4y + 1 - m^{2} = 0 có \Delta' = ( - 2)^{2} - 3\left( 1 - m^{2} ight) = 3m^{2} + 1 > 0;\forall m

    Suy ra phương trình 3y^{2} - 4y + 1 - m^{2} = 0 luôn có hai nghiệm phân biệt. Do đó:

    \Leftrightarrow \frac{2 - \sqrt{3m^{2} + 1}}{3} \leq \frac{2 + \sqrt{3m^{2} + 1}}{3}

    Suy ra \max y = \frac{2 + \sqrt{3m^{2} + 1}}{3}. Theo yêu cầu bài toán ta có:

    \max y < 2 \Leftrightarrow \frac{2 + \sqrt{3m^{2} + 1}}{3} < 2

    \Leftrightarrow \sqrt{3m^{2} + 1} < 4 \Leftrightarrow 3m^{2} + 1 < 16 \Leftrightarrow - \sqrt{5} < m < \sqrt{5}

    Mà m\mathbb{\in Z} suy ra m \in \left\{ - 2; - 1;0;1;2 ight\}

    Vậy có tất cả 5 giá trị nguyên của tham số m thỏa mãn.

  • Câu 11: Vận dụng
    Ghi đáp án vào ô trống

    Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là f(t) = 4t^{3} - \frac{t^{4}}{2}(người). Nếu xem f'(t) là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ mấy?

    Đáp án: Ngày thứ 4||tư

    Đáp án là:

    Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là f(t) = 4t^{3} - \frac{t^{4}}{2}(người). Nếu xem f'(t) là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ mấy?

    Đáp án: Ngày thứ 4||tư

    Điều kiện t \geq 0.

    Ta có g(t) = f'(t) = 12t^{2} - 2t^{3}, g'(t) = 24t - 6t^{2}, g'(t) = 0 \Leftrightarrow \left\lbrack \begin{matrix} t = 0 \\ t = 4 \\ \end{matrix} ight..

    Bảng biến thiên:

    Vậy tốc độ truyền bệnh lớn nhất vào ngày thứ 4.

    Đáp số: 4.

  • Câu 12: Thông hiểu
    Chọn mệnh đề đúng

    Cho hàm số y = f(x) có bảng biến thiên trên \lbrack - 5;7) như sau:

    Mệnh đề nào dưới đây đúng?

    Hướng dẫn:

     Dựa vào bảng biến thiên trên \lbrack - 5;7) , ta có: \underset{\lbrack - 5;7)}{Min}f(x) = f(1) = 2 .

  • Câu 13: Vận dụng cao
    Ghi đáp án vào ô trống

    Hai thành phố A và B cách nhau một con sông. Người ta xây dựng một cây cầu EF bắc qua sông biết rằng thành phố A cách con sông một khoảng là 5km và thành phố B cách con sông một khoảng là 7km (hình vẽ), biết HE + KF = 24km và độ dài EF không đổi. Hỏi cần xây cây cầu cách thành phố B là bao nhiêu km để đường đi từ thành phố A đến thành phố B là ngắn nhất (đi theo đường AEFB) ? (kết quả làm tròn đến hàng đơn vị)

    Đáp án: 16 km

    Đáp án là:

    Hai thành phố A và B cách nhau một con sông. Người ta xây dựng một cây cầu EF bắc qua sông biết rằng thành phố A cách con sông một khoảng là 5km và thành phố B cách con sông một khoảng là 7km (hình vẽ), biết HE + KF = 24km và độ dài EF không đổi. Hỏi cần xây cây cầu cách thành phố B là bao nhiêu km để đường đi từ thành phố A đến thành phố B là ngắn nhất (đi theo đường AEFB) ? (kết quả làm tròn đến hàng đơn vị)

    Đáp án: 16 km

    Đặt HE = x_{}và_{}FK = y, với x,\ y > 0

    Ta có: HE + KF = 24 \Rightarrow x + y =24 \Rightarrow y = 24 - x

    \left\{ \begin{matrix}AE = \sqrt{25 + x^{2}} \\BF = \sqrt{49 + y^{2}} = \sqrt{49 + (24 - x)^{2}} \\\end{matrix} ight.

    Nhận định AB ngắn nhất khi AE + BF nhỏ nhất ( vì EF không đổi).

    Xét hàm số f(x) = \sqrt{x^{2} + 25} +\sqrt{(24 - x)^{2} + 49}

    f'(x) = \frac{x}{\sqrt{x^{2} + 25}} +\frac{x - 24}{\sqrt{x^{2} - 48x + 625}},\ \forall x \in(0;24).

    Cho f'(x) = 0 \Rightarrow x =10

    Bảng biến thiên

    Vậy\underset{(0;24)\ \ \ \ \ \ \ \ \ \}{\min f(x)} = f(10) = 12\sqrt{5}

    Khi đó BF = \sqrt{49 + (24 - 10)^{2}} =7\sqrt{5} \approx 16\ km

  • Câu 14: Vận dụng
    Xác định mệnh đề đúng

    Cho hàm số y = \frac{x + m}{x - 1} (với m là tham số thực) thỏa mãn \min_{\lbrack 2;4brack}y = 3. Mệnh đề nào dưới đây là đúng?

    Hướng dẫn:

    Đạo hàm f'(x) = - \frac{m + 1}{(x - 1)^{2}}.

    TH1. Với m > - \ 1 suy ra f'(x) = - \frac{m + 1}{(x - 1)^{2}} < 0;\ \ \forall x eq 1 nên hàm số f(x) nghịch biến trên mỗi khoảng xác định.

    Khi đó \min_{\lbrack 2;4brack}y = f(4) = \frac{m + 4}{3} = 3 \Leftrightarrow m = 5 (thỏa mãn).

    TH2. Với m < - 1 suy ra f'(x) = - \frac{m + 1}{(x - 1)^2} > 0;\ \ \forall x eq 1 nên hàm số f(x) đồng biến trên mỗi khoảng xác định.

    Khi đó \min_{\lbrack 2;4brack}y = f(2) = m + 2 = 3 \Leftrightarrow m = 1 (Không thỏa mãn).

    Vậy m = 5 là giá trị cần tìm và thỏa mãn điều kiện m > 4.

  • Câu 15: Thông hiểu
    Tìm giá trị lớn nhất của tham số m

    Cho hàm số f(x) = \frac{x - m^{2}}{x + 8} với m là tham số thực. Tìm giá trị lớn nhất của m để hàm số có giá trị nhỏ nhất trên đoạn \lbrack 0;3brack bằng - 2.

    Hướng dẫn:

    Đạo hàm y' = \frac{8 + m^{2}}{(x + 8)^{2}} > 0,\ \forall x \in \lbrack 0;3brack.

    Suy ra hàm số f(x) đồng biến trên đoạn \lbrack 0;3brack

    \Rightarrow \min_{\lbrack 0;3brack}f(x) = f(0) = - \frac{m^{2}}{8}

    Thao bài ra: \min_{\lbrack 0;3brack}f(x) = - 2 \Leftrightarrow - \frac{m^{2}}{8} = - 2 \Leftrightarrow m = \pm 4

    Suy ra giá trị m lớn nhất là m = 4.

  • Câu 16: Thông hiểu
    Tìm các giá trị nguyên của tham số m

    Số các giá trị nguyên của tham số m để hàm số y = \frac{1}{3}x^{3} - x^{2} - 3x + 2m + 7 có giá trị nhỏ nhất trên đoạn \lbrack 2;4brack thuộc khoảng ( - 5;8) là:

    Hướng dẫn:

    Xét hàm số y = \frac{1}{3}x^{3} - x^{2} - 3x + 2m + 7 trên \lbrack 2;4brack ta có:

    y' = x^{2} - 2x - 3 \Rightarrow y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 1 \\ x = 3 \\ \end{matrix} ight.

    \Rightarrow \left\{ \begin{matrix}y(2) = - \dfrac{1}{3} + 2m \\y(4) = \dfrac{1}{3} + 2m \\y(3) = - 2 + 2m \\\end{matrix} ight.\ \Rightarrow \min_{\lbrack 2;4brack}y = - 2 + 2m\in ( - 5;8)

    \Leftrightarrow - 5 < - 2 + 2m < 8 \Leftrightarrow - 3 < 2m < 10 \Leftrightarrow - \frac{3}{2} < m < 5

    Mà m\mathbb{\in Z \Rightarrow}m \in \left\{ - 1;0;1;2;3;4 ight\}

    Vậy có tất cả 6 giá trị nguyên của tham số m thỏa mãn yêu cầu.

  • Câu 17: Thông hiểu
    Chọn đáp án thích hợp

    Một loại thuốc được dùng cho bệnh nhân và nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi công thức c(t) = \frac{t}{t^{2} + 1}(mg/L). Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất?

    Hướng dẫn:

    Ta có: c'(t) = \frac{- t^{2} + 1}{\left( t^{2} + 1 ight)^{2}};\forall t \in (0; + \infty). Cho c'(t) = 0 \Leftrightarrow \frac{- t^{2} + 1}{\left( t^{2} + 1 ight)^{2}} = 0 \Leftrightarrow \left\lbrack \begin{matrix} t = 1 \\ t = - 1 \\ \end{matrix} ight.

    Bảng biến thiên:

    Vậy sau khi tiêm 1 giờ, nồng độ thuốc trong máu bệnh nhân cao nhất.

  • Câu 18: Thông hiểu
    Tính giá trị biểu thức

    Tập giá trị của hàm số f(x) = x + \frac{9}{x} với x \in \lbrack 2;4brack là đoạn \lbrack a;bbrack. Tính P = b - a.

    Hướng dẫn:

    Ta có: f'(x) = 1 - \frac{9}{x^{2}} = \frac{x^{2} - 9}{x^{2}}

    ightarrow f'(x) = 0

    \Leftrightarrow x^{2} - 9 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 3 \in \lbrack 2;4brack \\ x = - 3 otin \lbrack 2;4brack \\ \end{matrix} ight.

    Ta có \left\{ \begin{matrix} f(2) = \frac{13}{2} \\ f(3) = 6 \\ f(4) = \frac{25}{4} \\ \end{matrix} ight. \Rightarrow \min_{\lbrack 2;4brack}f(x) = 6;\max_{\lbrack 2;4brack}f(x) = \frac{13}{2}

    \Rightarrow \lbrack a;bbrack = \left\lbrack 6;\frac{13}{2} ightbrack \Rightarrow P = b - a = \frac{13}{2} - 6 = \frac{1}{2}

  • Câu 19: Vận dụng cao
    Ghi đáp án vào ô trống

    Anh Hùng đang ở trong rừng để đào vàng và tìm thấy vàng ở điểm X cách điểm A một khoảng 3 km. Điểm A nằm trên đường bờ biển (đường bờ biển là đường thẳng). Trại của anh Hùng nằm ở vị trí Y cách điểm B một khoảng 3 km. Điểm B cũng thuộc đường bờ biển. Biết rằng AB = 3(km),AM = NB = x(km) và AX = BY = 3(km) (minh hoạ như hình vẽ sau).

    Khi đang đào vàng, anh Hùng không may bị rắn cắn, chất độc lan vào máu. Sau khi bị cắn, nồng độ chất độc trong máu tăng theo thời gian được tính theo phương trình y = 50\log(t +2). Trong đó, y là nồng độ, t là thời gian tính bằng giờ sau khi bị rắn cắn. Anh cần quay trở lại trại để lấy thuốc giải độc. Anh ấy chạy trong rừng và trên bãi biển với vận tốc lần lượt là 5km/h và 13km/h. Để về đến trại anh Hùng cần chạy từ trong rừng qua điểm M,N trên bãi biển. Tính nồng độ chất độc trong máu thấp nhất khi anh Hùng về đến trại (làm tròn đáp án đến hàng phần chục).

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Anh Hùng đang ở trong rừng để đào vàng và tìm thấy vàng ở điểm X cách điểm A một khoảng 3 km. Điểm A nằm trên đường bờ biển (đường bờ biển là đường thẳng). Trại của anh Hùng nằm ở vị trí Y cách điểm B một khoảng 3 km. Điểm B cũng thuộc đường bờ biển. Biết rằng AB = 3(km),AM = NB = x(km) và AX = BY = 3(km) (minh hoạ như hình vẽ sau).

    Khi đang đào vàng, anh Hùng không may bị rắn cắn, chất độc lan vào máu. Sau khi bị cắn, nồng độ chất độc trong máu tăng theo thời gian được tính theo phương trình y = 50\log(t +2). Trong đó, y là nồng độ, t là thời gian tính bằng giờ sau khi bị rắn cắn. Anh cần quay trở lại trại để lấy thuốc giải độc. Anh ấy chạy trong rừng và trên bãi biển với vận tốc lần lượt là 5km/h và 13km/h. Để về đến trại anh Hùng cần chạy từ trong rừng qua điểm M,N trên bãi biển. Tính nồng độ chất độc trong máu thấp nhất khi anh Hùng về đến trại (làm tròn đáp án đến hàng phần chục).

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 20: Thông hiểu
    Tìm giá trị lớn nhất của hàm số

    Tìm giá trị lớn nhất M của hàm số f(x) = x - \frac{1}{x} trên (0;3brack.

    Hướng dẫn:

    Đạo hàm f'(x) = 1 + \frac{1}{x^{2}} > 0,\ \forall x \in (0;3).

    Suy ra hàm số f(x) đồng biến trên (0;3brack nên đạt giá trị lớn nhất tại x = 3 và \max_{(0;3brack}f(x) = f(3) = \frac{8}{3}.

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (35%):
    2/3
  • Thông hiểu (40%):
    2/3
  • Vận dụng (25%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Tải file làm trên giấy
1
53 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này