Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập trắc nghiệm Toán 12 CTST Bài 2 (Mức độ Vừa)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Vận dụng
    Xác định vận tốc lớn nhất

    Người ta khảo sát gia tốc a(t) của một vật thể chuyển động (t là khoảng thời gian tính bằng giâu từ lúc vật thể chuyển động) từ giây thứ nhất đến giây thứ ba ghi nhận được a(t) là một hàm số liên tục có đồ thị như hình bên:

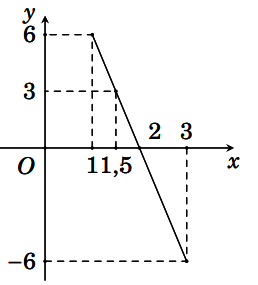
    Xác định vận tốc lớn nhất

    Hỏi trong thời gian từ giây thứ nhất đến giây thứ ba được khảo sát đó, thời điểm nào vận tốc lớn nhất?

    Gợi ý:

     Gợi ý: Mối quan hệ giữa gia tốc và vận tốc

    a\left( t ight) = v'\left( t ight)

    Hướng dẫn:

    Từ đồ thị ta có: a(t) = 0 => v’(t) = 0 = > t = 2

    Ta có bảng biến thiên:

    Xác định vận tốc lớn nhất

    => Vận tốc lớn nhất đạt được khi t = 2

  • Câu 2: Thông hiểu
    Tìm chi phí thấp nhất để xây dựng

    Gia đình bác T muốn xây một bình chứa hình trụ có thể tích 75m^{3}. Đáy làm bằng bê tông giá 100 nghìn đồng/m2, thành làm bằng tôn giá 90 nghìn đồng/m2, nắp bằng nhôm giá 140 nghìn đồng/m2. Vậy đáy của hình trụ có bán kính bằng bao nhiêu để chi phí xây dựng là thấp nhất?

    Hướng dẫn:

    Gọi x(m);(x > 0) là bán kính đáy của bình chứa hình trụ

    Khi đó tổng số tiền phải trả là 14.10^{4}.\pi x^{2} + 10^{5}.\pi x^{2} +\frac{144.9.10^{4}}{x}

    Đặt f(x) = 14.10^{4}.\pi x^{2} +10^{5}.\pi x^{2} + \frac{144.9.10^{4}}{x}

    \Rightarrow f'(x) = 48.10^{4}\pi x -\frac{1296.10^{4}}{x}

    \Rightarrow f'(x) = 0\Leftrightarrow 48.10^{4}\pi x - \frac{1296.10^{4}}{x} = 0\Leftrightarrow x = \frac{3}{\sqrt[3]{\pi}}

    Vậy để chi phí xây dựng là thấp nhất thì bán kính đáy bằng \frac{3}{\sqrt[3]{\pi}}m.

  • Câu 3: Thông hiểu
    Tìm số phần từ của tập hợp S

    Gọi S là tập hợp tất cả các giá trị thực của tham số m để hàm số y = \frac{\cos x + m^{2}}{2 - \cos x} có giá trị lớn nhất trên \left\lbrack - \frac{\pi}{2};\frac{\pi}{3} ightbrack bằng 1. Số phần tử của tập hợp S:

    Hướng dẫn:

    Ta có: y = \frac{\cos x + m^{2}}{2 - \cos x};\forall x \in \left\lbrack - \frac{\pi}{2};\frac{\pi}{3} ightbrack

    Đặt t = \cos x;(0 \leq t \leq 1)

    Hàm số đã cho trở thành: f(t) = \frac{t + m^{2}}{2 - t};\forall t \in \lbrack 0;1brack

    Ta có: f'(t) = \frac{2 + m^{2}}{(2 - t)^{2}} > 0;\forall t \in \lbrack 0;1brack

    \Rightarrow \underset{\left\lbrack - \frac{\pi}{2};\frac{\pi}{3} ightbrack}{\max y} = f(1) = m^{2} + 1 = 1 \Leftrightarrow m = 0

    Vậy số phần tử của tập hợp S là 1.

  • Câu 4: Thông hiểu
    Chọn đáp án thích hợp

    Độ giảm huyết áp của một bệnh nhân G(x) = 0,025x^{2}(30 - x) trong đó x là số miligam thuộc được tiêm cho bệnh nhân (0 < x < 30). Để bệnh nhân đó có huyết áp giảm nhiều nhất thì liều lượng thuốc cần tiêm vào là:

    Hướng dẫn:

    Ta có: G(x) = 0,025x^{2}(30 - x) \Rightarrow G'(x) = 1,5x - 0,075x^{2}

    \Rightarrow G'(x) = 0 \Leftrightarrow 1,5x - 0,075x^{2} = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = 20 \\ \end{matrix} ight.

    Ta có bảng biến thiên như sau:

    Vậy để bệnh nhân đó có huyết áp giảm nhiều nhất thì lượng thuốc cần tiêm vào là x = 20(mg).

  • Câu 5: Thông hiểu
    Ghi đáp án vào ô trống

    Một hãng điện thoại đưa ra quy luật bán buôn cho từng đại lí, đó là đại lí càng nhập nhiều chiếc điện thoại của hãng thì giá bán buôn một chiếc điện thoại càng giảm. Cụ thể, nếu đại lí mua x điện thoại thì giá tiền của mỗi điện thoại là 4000-2x(nghìn đồng), x \in N^{*},x < 2000. Đại lí nhập cùng một lúc bao nhiêu chiếc điện thoại thì hãng có thể thu về nhiều tiền nhất từ đại lí đó?

    Đáp án: 1000||1 000

    Đáp án là:

    Một hãng điện thoại đưa ra quy luật bán buôn cho từng đại lí, đó là đại lí càng nhập nhiều chiếc điện thoại của hãng thì giá bán buôn một chiếc điện thoại càng giảm. Cụ thể, nếu đại lí mua x điện thoại thì giá tiền của mỗi điện thoại là 4000-2x(nghìn đồng), x \in N^{*},x < 2000. Đại lí nhập cùng một lúc bao nhiêu chiếc điện thoại thì hãng có thể thu về nhiều tiền nhất từ đại lí đó?

    Đáp án: 1000||1 000

    Số tiền hãng thu được khi đại lí nhập x chiếc điện thoại là f(x) = x(4000 - 2x).

    Ta có: f'(x) = - \ 4x + 4000.

    Khi đó, f'(x) = 0 \Leftrightarrow x = 1\ 000 \Rightarrow f(x) = 2000000

    Học sinh tự vẽ bảng biến thiên

    Ta suy ra:

    Đại lí nhập cùng lúc 1\ 000 chiếc điện thoại thì hãng có thể thu nhiều tiền nhất từ đại lí đó với 2 000 000 000(đồng).

    Đáp số: 1000.

  • Câu 6: Nhận biết
    GTLN của hàm số trên khoảng là bao nhiêu?

    Cho hàm số y = f(x) và có bảng biến thiên trên [-2; 3) như sau:

    GTLN của hàm số trên khoảng là bao nhiêu?

    Giá trị lớn nhất của hàm số trên đoạn [-2; 3] bằng:

    Hướng dẫn:

    Từ đồ thị của hàm số y = f(x) ta thấy hàm số y = f(x) xác định và liên tục trên đoạn [-2; 3]

    Ta có: f(x) ∈ [-2; 3] với \forall x \in \mathbb{R} => \mathop {\max }\limits_{\left[ { - 2;3} ight]} f\left( x ight) = f\left( 3 ight) = 4

  • Câu 7: Thông hiểu
    Tìm tham số m thỏa mãn yêu cầu

    Tìm giá trị nhỏ nhất m của hàm số f(x) = x^{2} + \frac{2}{x} trên khoảng (0; + \infty).

    Hướng dẫn:

    Ta có :

    f'(x) = 2x - \frac{2}{x^{2}} = \frac{2\left( x^{3} - 1 ight)}{x^{2}}

    \Rightarrow f'(x) = 0 \Leftrightarrow x = 1 \in (0; + \infty)

    Lập bảng biến thiên & dựa vào bảng biến thiên ta thấy \min_{(0; + \infty)}f(x) = f(1) = 3.

  • Câu 8: Thông hiểu
    Định tập giá trị T của hàm số

    Tìm tập giá trị T của hàm số f(x) = x^{2} + \frac{2}{x} với x \in \lbrack 3;5brack.

    Hướng dẫn:

    Đạo hàm f'(x) = 2x - \frac{2}{x^{2}}= \frac{2\left( x^3 - 1 ight)}{x^{2}} > 0,\ \forall x \in(3;5)

    Suy ra hàm số đồng biến trên [3;5] nên \left\{ \begin{matrix} \min_{\lbrack 3;5brack}f(x) = f(3) = \frac{29}{3} \\ \max_{\lbrack 3;5brack}f(x) = f(5) = \frac{127}{5} \\ \end{matrix} ight.

    Vậy tập giá trị của hàm số là đoạn \left\lbrack \frac{29}{3};\ \frac{127}{5} ightbrack.

  • Câu 9: Thông hiểu
    Tìm GTLN của hàm số

    Cho hàm số y = {x^3} - \frac{3}{2}{x^2} + 1. Gọi M là giá trị lớn nhất của hàm số trên khoảng \left( { - 25;\frac{{11}}{{10}}} ight). Tìm M.

    Hướng dẫn:

    Ta có:

    \begin{matrix} y' = 3{x^2} - 3x \hfill \\ y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 1} \\ {x = 0} \end{array}} ight. \hfill \\ \end{matrix}

    Ta có bảng biến thiên

    Tìm GTLN của hàm số

    Từ bảng biến thiên ta có M = 1

  • Câu 10: Thông hiểu
    Tìm giá trị thực của tham số

    Tìm giá trị thực của tham số a để hàm số f(x) = - x^{3} - 3x^{2} + a có giá trị nhỏ nhất trên đoạn \lbrack - 1;1brack bằng 0.

    Hướng dẫn:

    Đạo hàm f'(x) = - 3x^{2} - 6x

    \Rightarrow f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \in \lbrack - 1;1brack \\ x = - 2 otin \lbrack - 1;1brack \\ \end{matrix} ight.

    Ta có \left\{ \begin{matrix} f( - 1) = a - 2 \\ f(0) = a \\ f(1) = a - 4 \\ \end{matrix} ight. \Rightarrow \min_{\lbrack - 1;1brack}f(x) = f(1) = a - 4

    Theo bài ra: \min_{\lbrack - 1;1brack}f(x) = 0 \Leftrightarrow a - 4 = 0 \Leftrightarrow a = 4

  • Câu 11: Nhận biết
    Chọn mệnh đề đúng

    Cho hàm số y = f(x) liên tục trên \mathbb{R} và có bảng biến thiên như sau:

    Mệnh đề nào sau dây đúng?

    Hướng dẫn:

    Từ bảng biến thiên ta thấy hàm số có GTLN bằng 2 và không có GTNN.

  • Câu 12: Nhận biết
    Chọn câu đúng

    Cho hàm số y = f(x) xác định, liên tục trên \mathbb{R} và có bảng biến thiên như sau:

    Chọn câu đúng

    Khẳng định nào sau đây là đúng?

    Hướng dẫn:

    Từ bảng biến thiên, ta dễ dàng thấy được A, B, D sai, C đúng

  • Câu 13: Thông hiểu
    Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số

    Cho hàm số y = f(x) xác định và liên tục trên \mathbb{R} có đồ thị như hình vẽ bên. Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f(x) trên đoạn \lbrack - 2\ ;\ 2brack.

    Hướng dẫn:

    Nhìn vào đồ thị ta thấy:

    M = \max_{\lbrack - 2\ ;\ 2brack}f(x) = - 1 khi x = - 1 hoặc x = 2.

    m = \min_{\lbrack - 2\ ;\ 2brack}f(x) = - 5 khi x = - 2 hoặc x = 1.

  • Câu 14: Thông hiểu
    Chọn đáp án đúng:

    Giá trị lớn nhất của hàm số y = f(x) = 2x^{3} + 3x^{2} - 12x + 2 trên đoạn [-1;2] có giá trị là một số thuộc khoảng nào dưới đây?

  • Câu 15: Nhận biết
    Cho hàm số y = f(x) có đồ thị sau:

    Toán 12 bài 2

    Giá trị nhỏ nhất của hàm số trên đoạn [0;2] là:

  • Câu 16: Thông hiểu
    Tính tổng min max của hàm số trên đoạn cho trước

    Cho hàm số y = f(x) liên tục và có đồ thị trên đoạn \lbrack - 2;\ 4brack như hình vẽ bên. Tổng giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên đoạn \lbrack - 2;\ 4brack bằng

    Hướng dẫn:

    Dựa vào đồ thị hàm số ta có

    m = \underset{x \in \lbrack - 2\ ;\ 4brack}{Min}f(x) = - 4, M = \underset{x \in \lbrack - 2\ ;\ 4brack}{Max}f(x) = 7

    Khi đó M + m = 3

  • Câu 17: Thông hiểu
    Xác định min max của hàm số trên đoạn

    Cho hàm số y = f(x) xác định và liên tục trên \mathbb{R}, có đồ thị như hình vẽ bên.

    Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = f(x) trên đoạn \lbrack - 2;2brack.

    Hướng dẫn:

    Nhận thấy trên đoạn \lbrack - 2;2brack

    Đồ thị hàm số có điểm thấp nhất có tọa độ ( - 2; - 5) và (1; - 5)

    \overset{}{ightarrow} Giá trị nhỏ nhất của hàm số này trên đoạn \lbrack - 2;2brack bằng - 5.

    Đồ thị hàm số có điểm cao nhất có tọa độ ( - 1; - 1) và (2; - 1)

    \overset{}{ightarrow} Giá trị lớn nhất của hàm số này trên đoạn \lbrack - 2;2brack bằng - 1.

  • Câu 18: Thông hiểu
    Tính giá trị của biểu thức

    Cho hàm số y = f(x) liên tục trên đoạn \lbrack - 1;3brack và có đồ thị như hình vẽ bên. Gọi M,mlần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \lbrack - 1;3brack. Giá trị của M + m là

    Hướng dẫn:

    Dựa vào đồ thị ta thấy GTLN của hàm số trên đoạn \lbrack - 1;3brack là M = 2 đạt được tại x = - 1 và GTNN của hàm số số trên đoạn \lbrack - 1;3bracklà m = - 4 đạt được tại x = 2

    \Rightarrow M + m = 2 + ( - 4) = - 2

  • Câu 19: Thông hiểu
    Xác định giá trị tham số m thỏa mãn yêu cầu

    Cho hàm số y = - x^{3} + 6(m + 2)x^{2} - m + 1 với m là tham số. Tìm tất cả các giá trị của tham số m để hàm số đã cho đồng biến trên ( - 2; - 1)?

    Hướng dẫn:

    Ta có: y' = - 3x^{2} + 12(m + 2)x

    Hàm số y = - x^{3} + 6(m + 2)x^{2} - m + 1 đồng biến trên khoảng ( - 2; - 1) khi và chỉ khi:

    y' = - 3x^{2} + 12(m + 2)x \geq 0;\forall x \in ( - 2; - 1)

    \Leftrightarrow - x^{2} + 4mx + 8x \geq 0;\forall x \in ( - 2; - 1)

    \Leftrightarrow 4mx \geq x^{2} - 8x;\forall x \in ( - 2; - 1)

    \Leftrightarrow m \leq \frac{x}{4} - 2 \Leftrightarrow m \leq \frac{- 2}{4} - 2 = - \frac{5}{2}

    Vậy đáp án cần tìm là m \in \left( - \infty; - \frac{5}{2} ightbrack.

  • Câu 20: Thông hiểu
    Xét tính đúng sai của các khẳng định

    Một chất điểm chuyển động theo phương trình S = - t^{3} + 9t^{2} + 21t + 9 trong đó t tính bằng giây (s) và S tính bằng mét (m). Xét tính đúng sai của các khẳng định sau.

    a) v(t) = - 3t^{2} + 18t + 2. Sai||Đúng

    b) Vận tốc của chất điểm tại giây thứ 2 là 45\ m/s. Đúng||Sai

    c) Vận tốc của chất điểm tại thời điểm gia tốc triệt tiêu là 45\ m/s. Sai||Đúng

    d) Vận tốc chuyển động đạt giá trị lớn nhất tại thời điểm t = 3\ \ (s). Đúng||Sai

    Đáp án là:

    Một chất điểm chuyển động theo phương trình S = - t^{3} + 9t^{2} + 21t + 9 trong đó t tính bằng giây (s) và S tính bằng mét (m). Xét tính đúng sai của các khẳng định sau.

    a) v(t) = - 3t^{2} + 18t + 2. Sai||Đúng

    b) Vận tốc của chất điểm tại giây thứ 2 là 45\ m/s. Đúng||Sai

    c) Vận tốc của chất điểm tại thời điểm gia tốc triệt tiêu là 45\ m/s. Sai||Đúng

    d) Vận tốc chuyển động đạt giá trị lớn nhất tại thời điểm t = 3\ \ (s). Đúng||Sai

    a) v(t) = S'(t) = - 3t^{2} + 18t + 21 nên a sai.

    b) Ta có: v(t) = S'(t) = - 3t^{2} + 18t + 2\overset{}{ightarrow}v(2) = 45\ m/s. nên b) đúng

    c) Ta có: a(t) = v'(t) = - 6t + 18 = 0 \Leftrightarrow t = 3\overset{}{ightarrow}v(3) = 48\ m/s. nên c) sai

    Vận tốc v(t) = S'(t) = - 3t^{2} + 18t + 21 = - 3(t - 3)^{2} + 48 \leq 48.

    Vậy \max v(t) = 48 khi t = 3.

    Vận tốc chuyển động đạt giá trị lớn nhất khi t = 3\ \ (s). nên d) đúng.

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (20%):
    2/3
  • Thông hiểu (75%):
    2/3
  • Vận dụng (5%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
1
15 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Lớp 12
Xem thêm