Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau:
a) Có 6 thửa ruộng đã được khảo sát. Sai||Đúng
b) Khoảng biến thiên của mẫu số liệu trên là 1,2 (tấn/ha). Đúng||Sai
c) Khoảng tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là . Đúng||Sai
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là . Đúng||Sai
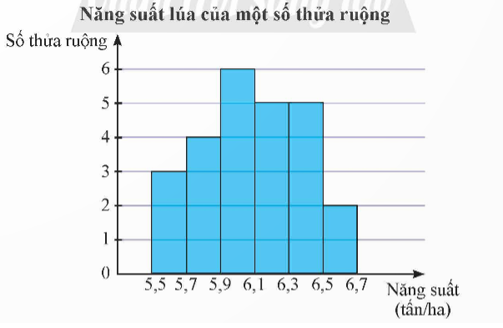
Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau:

a) Có 6 thửa ruộng đã được khảo sát. Sai||Đúng
b) Khoảng biến thiên của mẫu số liệu trên là 1,2 (tấn/ha). Đúng||Sai
c) Khoảng tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là . Đúng||Sai
d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là . Đúng||Sai
|
A. |
B. |
C. |
D. |
|
SAI |
ĐÚNG |
ĐÚNG |
ĐÚNG |
a) Số thửa ruộng được khảo sát là: n = 3 + 4 + 6 + 5 + 5 + 2 = 25.
b) Từ biểu đồ, ta có bảng tần số ghép nhóm của mẫu số liệu như sau:
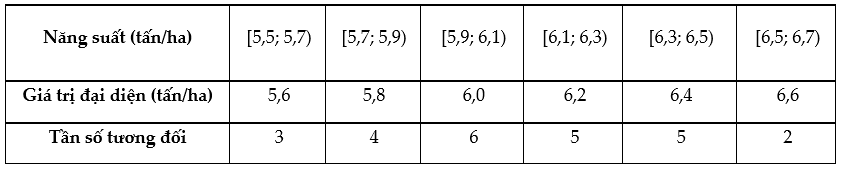
Khoảng biến thiên của mẫu số liệu đã cho là: R = 6,7 – 5,5 = 1,2 (tấn/ha).
c) Cỡ mẫu n = 25.
Gọi là mẫu số liệu gốc về năng suất của một số thửa ruộng được khảo sát được xếp theo thứ tự không giảm.
Ta có
[5,5; 5,7),
[5,7; 5,9),
[5,9; 6,1),
[6,1; 6,3),
[6,3; 6,5),
[6,5; 6,7).
Tứ phân vị thứ nhất của mẫu số liệu gốc là [5,7; 5,9).
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
d) Tứ phân vị thứ ba của mẫu số liệu gốc là [6,3; 6,5).
Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: