Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập trắc nghiệm Toán 12 Cánh Diều Bài 3 (Mức độ Dễ)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Nhận biết
    Chọn đáp án đúng

    Tiệm cận đứng của đồ thị hàm số y = \frac{x + 1}{x + 3} là

    Hướng dẫn:

    Ta có \lim_{x ightarrow - 3^{+}}y = -\infty và \lim_{x ightarrow -3^{-}}y = + \infty nên đồ thị hàm số nhận đường thẳng x = - 3 làm tiệm cận đứng.

  • Câu 2: Nhận biết
    Xác định tiệm cận của đồ thị hàm số

    Một đường tiệm cận đứng của đồ thị hàm số y = \frac{x^{2} + 4x + 3}{(x - 2)\left( x^{2} - 1 ight)} là:

    Hướng dẫn:

    Ta có:

    \lim_{x ightarrow 1^{+}}y = \lim_{x ightarrow 1^{+}}\frac{x^{2} + 4x + 3}{(x - 2)\left( x^{2} - 1 ight)} = \lim_{x ightarrow 1^{+}}\frac{x + 3}{(x - 2)(x - 1)} = - \infty

    \lim_{x ightarrow 2^{+}}y = \lim_{x ightarrow 2^{+}}\frac{x^{2} + 4x + 3}{(x - 2)\left( x^{2} - 1 ight)} = \lim_{x ightarrow 2^{+}}\frac{x + 3}{(x - 2)(x - 1)} = + \infty

    Vậy một đường tiệm cận đứng của đồ thị hàm số là x = 1.

  • Câu 3: Thông hiểu
    Chọn khẳng định sai

    Cho hàm số y = \frac{{x + 2}}{{x - 3}}. Khẳng định nào sau đây sai?

    Gợi ý:

    Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:

    \mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x ight) = \pm \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f\left( x ight) = \pm \infty

    Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:

    \mathop {\lim }\limits_{x \to + \infty } f\left( x ight) = {y_0};\mathop {\lim }\limits_{x \to - \infty } f\left( x ight) = {y_0}

    Hướng dẫn:

    Ta có tiệm cận đứng của hàm số là y = 3 và tiệm cận ngang là y = 1

    Giao điểm của hai đường tiệm cận I(3; 1) là tâm đối xứng của đồ thị

    => A, C, D đúng và B sai

  • Câu 4: Nhận biết
    Xác định tất cả các khẳng định sai

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Có bao nhiêu khẳng định sai trong các khẳng định dưới đây?

    (i) Đồ thị hàm số có ba đường tiệm cận.

    (ii) Hàm số có cực tiểu tại x = 2.

    (iii) Hàm số nghịch biến trên mỗi khoảng ( - \infty; - 1);(1; + \infty).

    (iv) Hàm số xác định trên \mathbb{R}.

    Hướng dẫn:

    Do \lim_{x ightarrow - \infty}f(x) = - 1;\lim_{x ightarrow + \infty}f(x) = 2 nên đồ thị hàm số có hai đường tiệm cận ngang; \lim_{x ightarrow 1^{\pm}}f(x) = \pm \infty nên đồ thị hàm số có một tiệm cận đứng. Do đó đồ thị hàm số có ba đường tiệm cận nên (i) đúng.

    Hàm số có cực tiểu tại x = 2 đúng nên (ii) đúng.

    Hàm số nghịch biến trên ( - \infty; - 1);(1;2) nên (iii) sai.

    Hàm số không xác định tại x = 1 nên (iv) sai.

    Vậy có 2 khẳng định sai.

  • Câu 5: Nhận biết
    Tìm tiệm cận đứng đường thẳng

    Tiệm cận đứng của đồ thị hàm số y = \frac{2x - 1}{- x + 2} là  đường thẳng

    Hướng dẫn:

    Ta có \lim_{x ightarrow 2^{+}}\frac{2x - 1}{- x + 2} = - \ \infty nên đồ thị hàm số có tiệm cận đứng là x = 2.

  • Câu 6: Thông hiểu
    Tìm số đường tiệm cận của đồ thị hàm số

    Cho hàm số y = f(x) có bảng biến như sau:

    Số đường tiệm cận của đồ thị hàm số là:

    Hướng dẫn:

    Từ bảng biến thiên của hàm số ta có:

    +\lim_{x ightarrow - \infty}y = 0;\lim_{x ightarrow + \infty}y = 0 \Rightarrowđồ thị hàm số nhận đường thẳng y = 0 là tiệm cận ngang.

    +\lim_{x ightarrow ( - 3)^{-}}y = + \infty;\lim_{x ightarrow ( - 3)^{+}} = - \infty \Rightarrowđồ thị hàm số nhận đường thẳng x = - 3 là tiệm cận đứng.

    +\lim_{x ightarrow 3^{-}}y = + \infty;\lim_{x ightarrow 3^{+}} = - \infty \Rightarrowđồ thị hàm số nhận đường thẳng x = 3là tiệm cận đứng.

    Vậy số đường tiệm cận của đồ thị hàm số là 3.

  • Câu 7: Nhận biết
    Chọn đáp án đúng

    Đường tiệm cận ngang của đồ thị hàm số y = \frac{- x - 1}{x + 3} cắt đường thẳng y = 2021x tại điểm có tung độ bằng:

    Hướng dẫn:

    Do \lim_{x ightarrow + \infty}\frac{- x- 1}{x + 3} = \lim_{x ightarrow + \infty}\dfrac{- 1 - \dfrac{1}{x}}{1 +\dfrac{3}{x}} = - 1 và \lim_{xightarrow - \infty}\frac{- x - 1}{x + 3} = \lim_{x ightarrow -\infty}\dfrac{- 1 - \dfrac{1}{x}}{1 + \dfrac{3}{x}} = - 1 nên đồ thị hàm số có đường tiệm cận ngang là y = - 1.

    Xét phương trình có hoành độ giao điểm 2021x = - 1 \Leftrightarrow x = \frac{- 1}{2021}

    Vậy tung độ giao điểm là y = - 1.

  • Câu 8: Nhận biết
    Chọn đáp án đúng

    Tiệm cận đứng của đồ thị hàm số y =\frac{x - 1}{x - 3} là

    Hướng dẫn:

    Ta có:

    \lim_{x ightarrow 3^{-}}\frac{x - 1}{x- 3} = - \infty. Suy ta tiệm cận đứng là đường thẳng x = 3.

  • Câu 9: Nhận biết
    Chọn đáp án thích hợp

    Cho hàm số y = \frac{ax^{2} + bx + c}{mx + n},(am eq 0) có đồ thị như hình vẽ. Phương trình đường tiệm cận xiên của đồ thị hàm số đã cho là:

    Hướng dẫn:

    Dựa vào đồ thị hàm số, ta thấy đường tiệm cận xiên của đồ thị hàm số đi qua 2 điểm (1;1) và ( - 1; - 1) nên đường tiệm cận xiên của đồ thị hàm số có phương trình y = x.

  • Câu 10: Nhận biết
    Xác định đường tiệm cận ngang

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Đồ thị hàm số có đường tiệm cận ngang là:

    Hướng dẫn:

    Dựa vào bảng biến thiên ta có: \lim_{x ightarrow \pm \infty}f(x) = 2 nên đồ thị hàm số có đường tiệm cận ngang là y = - 2.

  • Câu 11: Nhận biết
    Tìm số đường tiệm cận

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Đồ thị của hàm số đã cho có bao nhiêu tiệm cận?

    Hướng dẫn:

    Đồ thị của hàm số đã cho có 2 đường tiệm cận.

  • Câu 12: Nhận biết
    Tìm tọa độ điểm A

    Hai đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = \frac{2x - 5}{4 - x} cắt nhau tại điểm M. Xác định tọa độ điểm M?

    Hướng dẫn:

    Đồ thị hàm số y = \frac{2x - 5}{4 - x} có đường tiệm cận đứng x = 4 và đường tiệm cận ngang y = - 2. Do đó giao điểm của hai đường tiệm cận là M(4; - 2).

  • Câu 13: Thông hiểu
    Tìm các tiệm cận của đồ thị hàm số

    Đồ thị hàm số y = \frac{\sqrt{x^{2} - 3x - 10}}{x - 2} có bao nhiêu đường tiệm cận?

    Hướng dẫn:

    Điều kiện xác định \left\{ \begin{matrix} x^{2} - 3x - 10 \geq 0 \\ x - 2 eq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} \left\lbrack \begin{matrix} x \leq - 2 \\ x \geq 5 \\ \end{matrix} ight.\ \\ x eq 2 \\ \end{matrix} ight.\ \Leftrightarrow \left\lbrack \begin{matrix} x \leq - 2 \\ x \geq 5 \\ \end{matrix} ight.

    Vậy D = ( - \infty; - 2brack \cup \lbrack 5; + \infty)

    Xét \lim_{x ightarrow +\infty}\dfrac{\sqrt{x^{2} - 3x - 10}}{x - 2} = \lim_{x ightarrow +\infty}\dfrac{x\sqrt{1 - \dfrac{3}{x} - \dfrac{10}{x^{2}}}}{x - 2}=\lim_{x ightarrow + \infty}\dfrac{\sqrt{1 - \dfrac{3}{x} -\dfrac{10}{x^{2}}}}{1 - \dfrac{2}{x}} = 1

    Vậy y = 1 là tiệm cận ngang của đồ thị hàm số.

    Xét \lim_{x ightarrow -\infty}\dfrac{\sqrt{x^{2} - 3x - 10}}{x - 2} = \lim_{x ightarrow -\infty}\dfrac{- x\sqrt{1 - \dfrac{3}{x} - \dfrac{10}{x^{2}}}}{x - 2}=\lim_{x ightarrow + \infty}\dfrac{- \sqrt{1 - \dfrac{3}{x} -\dfrac{10}{x^{2}}}}{1 - \dfrac{2}{x}} = - 1

    Vậy y = - 1 là tiệm cận ngang của đồ thị hàm số.

    Vì \lim_{x ightarrow 2^{+}}\frac{\sqrt{x^{2} - 3x - 10}}{x - 2};\lim_{x ightarrow 2^{-}}\frac{\sqrt{x^{2} - 3x - 10}}{x - 2} không tồn tại nên đồ thị hàm số đã cho không có tiệm cận đứng.

    Vậy đồ thị hàm số có 2 tiệm cận.

  • Câu 14: Nhận biết
    Tìm tiệm cận đứng của hàm số

    Tiệm cận đứng của đồ thị hàm số y = \frac{2x + 3}{x - 1} là đường thẳng có phương trình

    Hướng dẫn:

    Ta có:

    \lim_{x ightarrow 1^{+}}y = \lim_{x ightarrow 1^{+}}\frac{2x + 3}{x - 1} = + \infty \Rightarrow x = 1 là tiệm cận đứng của đồ thị hàm số.

    \lim_{x ightarrow 1^{-}}y = \lim_{xightarrow 1^{-}}\frac{2x + 3}{x - 1} = - \infty \Rightarrow x =1 là tiệm cận đứng của đồ thị hàm số.

  • Câu 15: Nhận biết
    Tiệm cận đứng của đồ thị hàm số

    Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số y = \frac{{2x + 1}}{{x + 1}}?

    Gợi ý:

    Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:

    \mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x ight) = \pm \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f\left( x ight) = \pm \infty

    Hướng dẫn:

    Xét phương trình x + 1 = 0 => x = -1

    Và \mathop {\lim }\limits_{x \to - {1^ + }} f\left( x ight) = + \infty => x = -1 là tiệm cận đứng của đồ thị hàm số.

  • Câu 16: Nhận biết
    Số đường tiệm cận của đồ thị hàm số

    Cho hàm số y = \frac{{\sqrt {{x^2} - 4} }}{{x - 1}}. Đồ thị hàm số có mấy đường tiệm cận?

    Gợi ý:

    Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:

    \mathop {\lim }\limits_{x \to {x_0}^ + } f\left( x ight) = \pm \infty ;\mathop {\lim }\limits_{x \to {x_0}^ - } f\left( x ight) = \pm \infty

    Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:

    \mathop {\lim }\limits_{x \to + \infty } f\left( x ight) = {y_0};\mathop {\lim }\limits_{x \to - \infty } f\left( x ight) = {y_0}

    Hướng dẫn:

    Tập xác định: D = \left( { - \infty ;2} ight] \cup \left[ {2; + \infty } ight)

    Ta thấy rằng x = 1 không thuộc D => Đồ thị hàm số không có tiệm cận đứng.

    \begin{matrix} \mathop {\lim }\limits_{x \to \infty } y = \mathop {\lim }\limits_{x \to \infty } \dfrac{{\sqrt {{x^2} - 4} }}{{x - 1}} = \mathop {\lim }\limits_{x \to \infty } \dfrac{{\left| x ight|\sqrt {1 - \dfrac{4}{{{x^2}}}} }}{{x\left( {1 - \dfrac{1}{x}} ight)}} = \mathop {\lim }\limits_{x \to \infty } \dfrac{{\left| x ight|}}{x} \hfill \\ = \left\{ {\begin{array}{*{20}{c}} {\mathop {\lim }\limits_{x \to + \infty } y = 1} \\ {\mathop {\lim }\limits_{x \to - \infty } y = - 1} \end{array}} ight. \hfill \\ \end{matrix}

    => y = 1 và y = -1 là hai tiệm cận ngang của đồ thị hàm số.

  • Câu 17: Nhận biết
    Xác định số tiệm cận đứng của hàm số

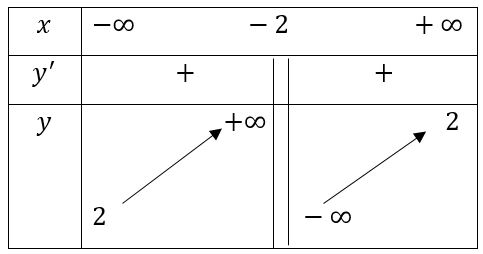
    Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây.

    Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận đứng?

    Hướng dẫn:

    Quan sát bảng biến thiên đã cho ta thấy:

    Đồ thị hàm số có hai đường tiệm cận đứng là hai đường thẳng có phương trình: x = - 2;x = 0.

  • Câu 18: Nhận biết
    Chọn đáp án đúng:

    Cho hàm số  y = \frac{\sqrt{5}x-2 }{x+1}

    Khẳng định nào sau đây đúng?

  • Câu 19: Nhận biết
    Tìm tiệm cận đứng của đồ thị hàm số

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Đồ thị hàm số có tiệm cận đứng là:

    Hướng dẫn:

    Từ bảng biến thiên ta có đồ thị hàm số có đường tiệm cận đứng là x = - 1.

  • Câu 20: Nhận biết
    Chọn khẳng định đúng

    Cho đồ thị hàm số y = f(x) như hình bên. Khẳng định nào sau đây là đúng?

    Hướng dẫn:

    Khẳng định đúng: “Đồ thị hàm số có tiệm cận đứng x = 0, tiệm cận ngang y = 1”.

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (85%):
    2/3
  • Thông hiểu (15%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Tải file làm trên giấy
1
29 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này