Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ Đang cập nhật

Trắc nghiệm Toán 12 Vectơ và các phép toán trong không gian (Mức Khó)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Vận dụng
    Tìm giá trị của k

    Gọi M,\ N lần lượt là trung điểm của các cạnh AC và BD của tứ diện ABCD. Gọi I là trung điểm đoạn MN và P là 1 điểm bất kỳ trong không gian. Tìm giá trị của k thích hợp điền vào đẳng thức vectơ: \overrightarrow{PI} = k\left( \overrightarrow{PA} + \overrightarrow{PB} + \overrightarrow{PC} + \overrightarrow{PD} \right).

    Hướng dẫn:

    Ta có \overrightarrow{PA} + \overrightarrow{PC} = 2\overrightarrow{PM}, \overrightarrow{PB} + \overrightarrow{PD} = 2\overrightarrow{PN}

    nên \overrightarrow{PA} + \overrightarrow{PB}\overrightarrow{+ PC} + \overrightarrow{PD} = 2\overrightarrow{PM} + 2\overrightarrow{PN}

    = 2(\overrightarrow{PM} + \overrightarrow{PN}) = 2.2.\overrightarrow{PI} = 4\overrightarrow{PI}

    Vậy k = \frac{1}{4}

  • Câu 2: Vận dụng cao
    Tìm giá trị nhỏ nhất của biểu thức

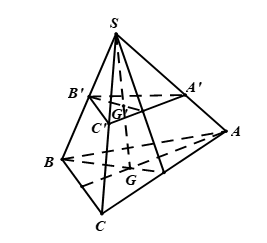
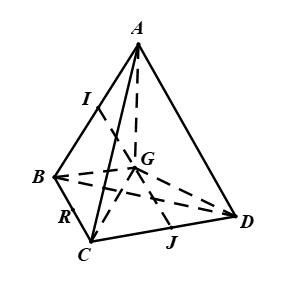
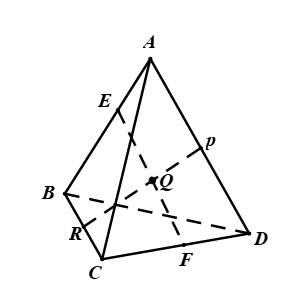
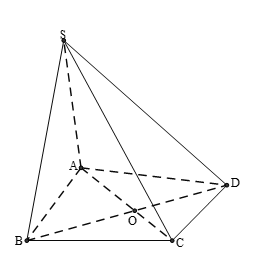
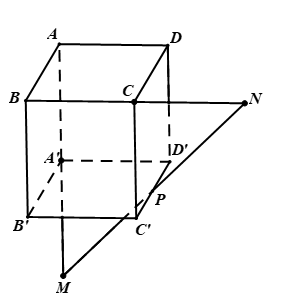
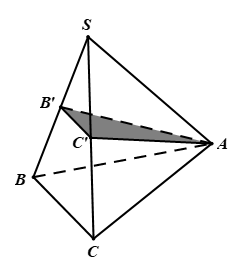
    Cho hình chóp S.ABC có SA = a,SB = b,SC = c. Một mặt phẳng (\alpha) luôn đi qua trọng tâm của tam giác ABC, cắt các cạnh SA,SB,SC lần lượt tại A',B',C'. Tìm giá trị nhỏ nhất của \frac{1}{SA'^{2}} + \frac{1}{SB'^{2}} + \frac{1}{SC'^{2}}.

    Hướng dẫn:

    Gọi G là trọng tâm của tam giác ABC. Ta có 3\overrightarrow{SG} = \overrightarrow{SA} + \overrightarrow{SB} + \overrightarrow{SC}

    = \frac{SA}{SA'}\overrightarrow{SA'} + \frac{SB}{SB'}\overrightarrow{SB'} + \frac{SC}{SC'}\overrightarrow{SC'}.

    Mà G,A',B',C' đồng phẳng nên \frac{SA}{SA'} +\frac{SB}{SB'} + \frac{SC}{SC'} = 3\Leftrightarrow\frac{a}{SA'} + \frac{b}{SB'} + \frac{c}{SC'} =3

    Theo BĐT Cauchy schwarz:

    Ta có \left( \frac{1}{SA'^{2}} + \frac{1}{SB'^{2}} + \frac{1}{SC'^{2}} \right)\left( a^{2} + b^{2} + c^{2} \right) \geq \left( \frac{a}{SA'} + \frac{b}{SB'} + \frac{c}{SC'} \right)^{2}

    \Leftrightarrow \frac{1}{SA'^{2}} + \frac{1}{SB'^{2}} + \frac{1}{SC'^{2}} \geq \frac{9}{a^{2} + b^{2} + c^{2}}.

    Đẳng thức xảy ra khi

    \frac{1}{aSA'} = \frac{1}{bSB'} = \frac{1}{cSC'} kết hợp với \frac{a}{SA'} + \frac{b}{SB'} + \frac{c}{SC'} = 3 ta được;

    SA' = \frac{a^{2} + b^{2} + c^{2}}{3a},SB' = \frac{a^{2} + b^{2} + c^{2}}{3b},SC' = \frac{a^{2} + b^{2} + c^{2}}{3c}.

    Vậy GTNN của \frac{1}{SA'^{2}} + \frac{1}{SB'^{2}} + \frac{1}{SC'^{2}} là \frac{9}{a^{2} + b^{2} + c^{2}}.

  • Câu 3: Vận dụng
    Tính giá trị biểu thức

    Cho tứ diện ABCD có AB;AC;AD đôi một vuông góc với nhau. Tính giá trị của biểu thức T = \left| \frac{\overrightarrow{AB}}{AB} + \frac{\overrightarrow{AC}}{AC} + \frac{\overrightarrow{AD}}{AD} ight|?

    Hướng dẫn:

    Vì các vectơ \frac{\overrightarrow{AB}}{AB};\frac{\overrightarrow{AC}}{AC};\frac{\overrightarrow{AD}}{AD} có độ dài bằng 1 và đôi một vuông góc với nhau nên

    \left( \frac{\overrightarrow{AB}}{AB} + \frac{\overrightarrow{AC}}{AC} + \frac{\overrightarrow{AD}}{AD} ight)^{2} = 3 \Leftrightarrow T = \left| \frac{\overrightarrow{AB}}{AB} + \frac{\overrightarrow{AC}}{AC} + \frac{\overrightarrow{AD}}{AD} ight| = \sqrt{3}

  • Câu 4: Vận dụng
    Xác định vị trí điểm M

    Trong không gian cho tam giác ABC. Tìm M sao cho giá trị của biểu thức P = MA^{2} + MB^{2} + MC^{2} đạt giá trị nhỏ nhất?

    Hướng dẫn:

    Gọi G là trọng tâm tam giác ABC

    Suy ra G cố định và \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0}

    P = MA^{2} + MB^{2} + MC^{2}

    P = \left( \overrightarrow{MG} + \overrightarrow{GA} ight)^{2} + \left( \overrightarrow{MG} + \overrightarrow{GB} ight)^{2} + \left( \overrightarrow{MG} + \overrightarrow{GC} ight)^{2}

    P = 3{\overrightarrow{MG}}^{2} + 2\overrightarrow{MG}.\left( \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} ight)^{2} + GA^{2} + GB^{2} + GC^{2}

    P = 3MG^{2} + GA^{2} + GB^{2} + GC^{2} \geq GA^{2} + GB^{2} + GC^{2}

    Dấu “=” xảy ra khi M \equiv G

    Vậy P_{\min} = GA^{2} + GB^{2} + GC^{2} với M \equiv G là trọng tâm tam giác ABC.

  • Câu 5: Vận dụng
    Chọn khẳng định sai

    Cho hình chóp S.ABCD. Gọi O là giao điểm của AC và BD. Trong các khẳng định sau, khẳng định nào sai?

    Hướng dẫn:

    Hình vẽ minh họa

    “Nếu \overrightarrow{SA} + \overrightarrow{SB} + 2\overrightarrow{SC} + 2\overrightarrow{SD} = 6\overrightarrow{SO} thì ABCD là hình thang » Đúng

    Vì \overrightarrow{SA} + \overrightarrow{SB} + 2\overrightarrow{SC} + 2\overrightarrow{SD} = 6\overrightarrow{SO} và SC\bot(BIH).

    Vì O,A,C và BIH thẳng hàng nên đặt \overrightarrow{OA} = k\overrightarrow{OC};OB = m\overrightarrow{OD}

    \Rightarrow (k + 1)\overrightarrow{OC} + (m + 1)\overrightarrow{OD} = \overrightarrow{0}.

    Mà \overrightarrow{OC},\overrightarrow{OD} không cùng phương nên k = - 2 và m = - 2

    \Rightarrow \frac{OA}{OC} = \frac{OB}{OD} = 2 \Rightarrow AB//CD.

    “Nếu ABCD là hình bình hành thì \overrightarrow{SA} + \overrightarrow{SB} + \overrightarrow{SC} + \overrightarrow{SD} = 4\overrightarrow{SO}.“. Đúng.

    Hs tự biến đổi bằng cách chêm điểm O vào vế trái.

    “Nếu ABCD là hình thang thì \overrightarrow{SA} + \overrightarrow{SB} + 2\overrightarrow{SC} + 2\overrightarrow{SD} = 6\overrightarrow{SO}. ». Sai.

    Vì nếu ABCD là hình thang cân có 2 đáy là AD,BC thì sẽ sai.

    “Nếu \overrightarrow{SA} + \overrightarrow{SB} + \overrightarrow{SC} + \overrightarrow{SD} = 4\overrightarrow{SO} thì ABCD là hình bình hành ». Đúng.

    Tương tự đáp án A với k = - 1,m = - 1 \Rightarrow O là trung điểm 2 đường chéo.

  • Câu 6: Vận dụng
    Xác định giá trị thực của k

    Gọi M;N lần lượt là trung điểm của các cạnh AC;BD của tứ diện ABCD. Gọi I là trung điểm của đoạn MN và P là một điểm bất kì trong không gian. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ \overrightarrow{PI} = k.\left( \overrightarrow{PA} + \overrightarrow{PB} + \overrightarrow{PC} + \overrightarrow{PD} ight)?

    Hướng dẫn:

    Hình vẽ minh họa

    Vì M;N lần lượt là trung điểm của các cạnh AC;BD nên ta có: \left\{ \begin{matrix} \overrightarrow{IA} + \overrightarrow{IC} = 2\overrightarrow{IM} \\ \overrightarrow{IB} + \overrightarrow{ID} = 2\overrightarrow{IN} \\ \end{matrix} ight..

    Mặt khác \overrightarrow{IM} + \overrightarrow{IN} = \overrightarrow{0} (vì I là trung điểm của MN) suy ra \overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} + \overrightarrow{ID} = \overrightarrow{0}

    Theo bài ra ta có:

    \overrightarrow{PA} + \overrightarrow{PB} + \overrightarrow{PC} + \overrightarrow{PD}

    = 4\overrightarrow{PI} + \overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} + \overrightarrow{ID} = 4\overrightarrow{PI}

    \Rightarrow 4k = 1 \Rightarrow k = \frac{1}{4}

  • Câu 7: Vận dụng
    Chọn mệnh đề đúng

    Cho tam giác ABC vuông tại A và có hai đỉnh B;C nằm trên mặt phẳng (P). Gọi A' là hình chiếu vuông góc của đỉnh A lên (P). Trong các mệnh đề sau, mệnh đề nào đúng?

    Hướng dẫn:

    Nếu A nằm trên (P) tức A’ trùng với A thì tam giác A’BC có góc A vuông, nếu A không nằm trên (P) thì

    \overrightarrow{A'B}.\overrightarrow{A'C} = \overrightarrow{A'A}.\overrightarrow{A'C} + \overrightarrow{AB}.\overrightarrow{A'C}

    = \overrightarrow{AB}.\overrightarrow{A'C} = \overrightarrow{AB}.\left( \overrightarrow{A'A} + \overrightarrow{AC} ight)

    = \overrightarrow{AB}.\overrightarrow{A'A} = - \overrightarrow{AB}.\overrightarrow{AA'} < 0 suy ra góc \widehat{BA'C} là góc tù.

  • Câu 8: Thông hiểu
    Tìm khẳng định đúng

    Cho tứ diện ABCD. Gọi M và P lần lượt là trung điểm của AB và CD. Đặt \overrightarrow{AB} = \overrightarrow{b},\overrightarrow{AC} = \overrightarrow{c},\overrightarrow{AD} = \overrightarrow{d}. Khẳng định nào sau đây đúng.

    Hướng dẫn:

    Ta có

    \overrightarrow{c} + \overrightarrow{d} - \overrightarrow{b} = \overrightarrow{AC} + \overrightarrow{AD} - \overrightarrow{AB}

    = 2\overrightarrow{AP} - 2\overrightarrow{AM} = 2\left( \overrightarrow{MP} ight)

    \Leftrightarrow \overrightarrow{MP} = \frac{1}{2}(\overrightarrow{c} + \overrightarrow{d} - \overrightarrow{b}).

  • Câu 9: Vận dụng
    Ghi đáp án vào ô trống

    Cho tứ diện ABCD và các điểm M;N xác định bởi \overrightarrow{AM} = 2\overrightarrow{AB} -3\overrightarrow{AC}(1),\overrightarrow{DN} = \overrightarrow{DB} +x\overrightarrow{DC}(2). Tìm x để các đường thẳng AD;BC;MN cùng song song với một mặt phẳng?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Cho tứ diện ABCD và các điểm M;N xác định bởi \overrightarrow{AM} = 2\overrightarrow{AB} -3\overrightarrow{AC}(1),\overrightarrow{DN} = \overrightarrow{DB} +x\overrightarrow{DC}(2). Tìm x để các đường thẳng AD;BC;MN cùng song song với một mặt phẳng?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 10: Thông hiểu
    Xác định góc giữa hai vectơ

    Cho tứ diện ABCD có AB = AC = AD và \widehat{BAC} = \widehat{BAD} = 60^{0}. Hãy xác định góc giữa cặp vectơ \overrightarrow{AB} và \overrightarrow{CD}?

    Hướng dẫn:

    Hình vẽ minh họa

    Ta có: \overrightarrow{AB}.\overrightarrow{CD} = \overrightarrow{AB}.\left( \overrightarrow{AD} - \overrightarrow{AC} ight) = \overrightarrow{AB}.\overrightarrow{AD} - \overrightarrow{AB}.\overrightarrow{AC}

    = \left| \overrightarrow{AB}ight|.\left| \overrightarrow{AD} ight|.\cos\left(\overrightarrow{AB};\overrightarrow{AD} ight) - \left|\overrightarrow{AB} ight|.\left| \overrightarrow{AC} ight|.\cos\left(\overrightarrow{AB};\overrightarrow{AC} ight)

    = \left| \overrightarrow{AB}ight|.\left| \overrightarrow{AD} ight|.\cos60^{0} - \left|\overrightarrow{AB} ight|.\left| \overrightarrow{AC}ight|.\cos60^{0}

    Mà AC = AD \Rightarrow \overrightarrow{AB}.\overrightarrow{CD} = 0 \Rightarrow \left( \overrightarrow{AB};\overrightarrow{CD} ight) = 90^{0}

  • Câu 11: Thông hiểu
    Chọn đáp án đúng

    Cho tứ diện ABCD. Gọi M;N lần lượt là trung điểm của các cạnh AB;CD. Tìm giá trị thực của k thỏa mãn đẳng thức vectơ \overrightarrow{MN} = k.\left( \overrightarrow{AC} + \overrightarrow{BD} ight)?

    Hướng dẫn:

    Hình vẽ minh họa

    Ta có N là trung điểm của CD nên \overrightarrow{MC} + \overrightarrow{MD} = 2\overrightarrow{MN}

    M là trung điểm của AB nên \overrightarrow{MA} + \overrightarrow{MB} = \overrightarrow{0}

    Suy ra \overrightarrow{MN} = \frac{1}{2}.\left( \overrightarrow{MC} + \overrightarrow{MD} ight)

    = \frac{1}{2}.\left( \overrightarrow{MA} + \overrightarrow{AC} + \overrightarrow{MB} + \overrightarrow{BD} ight)

    = \frac{1}{2}.\left( \overrightarrow{AC} + \overrightarrow{BD} ight)

    \Rightarrow \overrightarrow{MN} = \frac{1}{2}.\left( \overrightarrow{AC} + \overrightarrow{BD} ight) \Rightarrow k = \frac{1}{2}

  • Câu 12: Vận dụng cao
    Tìm k để các điểm đồng phẳng

    Cho tứ diện ABCD. Lấy các điểm M,N,P,Q lần lượt thuộc AB,BC,CD,DA sao cho \overrightarrow{AM} =\frac{1}{3}\overrightarrow{AB},\overrightarrow{BN} =\frac{2}{3}\overrightarrow{BC},\overrightarrow{AQ} =\frac{1}{2}\overrightarrow{AD},\overrightarrow{DP} =k\overrightarrow{DC}. Hãy xác định k để M,N,P,Q đồng phẳng.

    Hướng dẫn:

    Hình vẽ minh họa

    Cách 1.

    Ta có \overrightarrow{AM} = \frac{1}{3}\overrightarrow{AB} \Rightarrow \overrightarrow{BM} - \overrightarrow{BA} = - \frac{1}{3}\overrightarrow{BA}

    \Rightarrow \overrightarrow{BM} = \frac{2}{3}\overrightarrow{BA}.

    Lại có \overrightarrow{BN} = \frac{2}{3}\overrightarrow{BC} do đó MN//AC.

    Vậy nếu M,N,P,Q đồng phẳng thì (MNPQ) \cap (ACD) = PQ \parallel AC

    \Rightarrow \frac{PC}{PD} = \frac{QA}{QD} = 1 hay \overrightarrow{DP} = \frac{1}{2}\overrightarrow{DC} \Rightarrow k = \frac{1}{2}.

    Cách 2. Đặt \overrightarrow{DA} = \overrightarrow{a},\overrightarrow{DB} = \overrightarrow{b},\overrightarrow{DC} = \overrightarrow{c} thì không khó khăn ta có các biểu diễn

    \overrightarrow{MN} = - \frac{2}{3}\overrightarrow{a} + \frac{2}{3}\overrightarrow{b}, \overrightarrow{MP} = - \frac{2}{3}\overrightarrow{a} - \frac{1}{3}\overrightarrow{b} + k\overrightarrow{c}, \overrightarrow{MN} = - \frac{1}{6}\overrightarrow{a} - \frac{1}{3}\overrightarrow{b}

    Các điểm M,N,P,Q đồng phẳng khi và chỉ khi các vec tơ \overrightarrow{MN},\overrightarrow{MP},\overrightarrow{MQ} đồng phẳng \Leftrightarrow \exists x,y:\overrightarrow{MP} = x\overrightarrow{MN} + y\overrightarrow{MQ}

    \Leftrightarrow - \frac{2}{3}\overrightarrow{a} - \frac{1}{3}\overrightarrow{b} + k\overrightarrow{c} = x\left( - \frac{2}{3}\overrightarrow{a} + \frac{2}{3}\overrightarrow{c} \right) + y\left( - \frac{1}{6}\overrightarrow{a} - \frac{1}{3}\overrightarrow{b} \right)

    Do các vec tơ \overrightarrow{a},\overrightarrow{b,}\overrightarrow{c} không đồng phẳng nên điều này tương đương với

    \left\{ \begin{matrix} - \frac{2}{3}x - \frac{1}{6}y = - \frac{2}{3} \\ - \frac{1}{3}y = - \frac{1}{3} \\ \frac{2}{3}x = k \\ \end{matrix} \right.\ \Leftrightarrow x = \frac{3}{4},y = 1,k = \frac{1}{2}.

  • Câu 13: Vận dụng cao
    Tính x; y theo k để ba điểm thẳng hàng

    Cho hình hộp ABCD.A'B'C'D' và các điểm M,N,P xác định bởi

    \overrightarrow{MA} = k\overrightarrow{MB'}(k \neq 0),\overrightarrow{NB} = x\overrightarrow{NC'},\overrightarrow{PC} = y\overrightarrow{PD'}. Hãy tính x,y theo k để ba điểm M,N,P thẳng hàng.

    Hướng dẫn:

    Hình vẽ minh họa

    Đặt \overrightarrow{AD} = \overrightarrow{a},\overrightarrow{AB} = \overrightarrow{b},\overrightarrow{AA'} = \overrightarrow{c}.

    Từ giả thiết ta có :

    \overrightarrow{AM} = \frac{k}{k - 1}\left( \overrightarrow{b} + \overrightarrow{c} \right)\ \ \ (1)

    \overrightarrow{AN} = \overrightarrow{b}+ \frac{x}{x - 1}\left( \overrightarrow{a} + \overrightarrow{c} \right) (2)

    \overrightarrow{AP} = \overrightarrow{a} + \overrightarrow{b} +\frac{y}{y - 1}\left( \overrightarrow{c} - \overrightarrow{b}\right)(3)

    Từ đó ta có

    \overrightarrow{MN} =\overrightarrow{AN} - \overrightarrow{AM}= \frac{x}{x -1}\overrightarrow{a} - \frac{1}{k - 1}\overrightarrow{b} + \left(\frac{x}{x - 1} - \frac{k}{k - 1} \right)\overrightarrow{c}

    + \left( \frac{x}{x - 1} - \frac{y}{y - 1} \right)\overrightarrow{c}.

    \overrightarrow{MP} =\overrightarrow{AP} - \overrightarrow{AM}= \overrightarrow{a} -(\frac{y}{y - 1} + \frac{1}{k - 1})\overrightarrow{b} + \left(\frac{y}{y - 1} - \frac{k}{k - 1} \right)\overrightarrow{c}

    Ba điểm M,N,P thẳng hàng khi và chỉ khi tồn tại \lambda sao cho \overrightarrow{MN} = \lambda\overrightarrow{MP}\ \ (*).

    Thay các vectơ \overrightarrow{MN},\overrightarrow{MP} vào (*) và lưu ý \overrightarrow{a},\overrightarrow{b},\overrightarrow{c} không đồng phẳng ta tính được x = \frac{1 + k}{1 - k},y = - \frac{1}{k}.

  • Câu 14: Vận dụng
    Xác định góc giữa cặp vectơ

    Cho tứ diệnABCD có AB = AC = AD và \widehat{BAC} = \widehat{BAD} = 60^{0},\ \widehat{CAD} = 90^{0}. Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ \overrightarrow{AB} và \overrightarrow{IJ}?

    Hướng dẫn:

    Hình vẽ minh họa

    Xét tam giácICD có J là trung điểm đoạn CD.

    Ta có: \overrightarrow{I J} = \frac{1}{2}\left( \overrightarrow{IC} + \overrightarrow{ID} ight)

    Vì tam giác ABC có AB = AC và \widehat{BAC} = 60{^\circ}

    Nên tam giác ABC đều. Suy ra: CI\bot AB

    Tương tự ta có tam giác ABD đều nên DI\bot AB.

    Xét \overrightarrow{IJ}.\overrightarrow{AB} = \frac{1}{2}\left( \overrightarrow{IC} + \overrightarrow{ID} ight).\overrightarrow{AB}= \frac{1}{2}\overrightarrow{IC}.\overrightarrow{AB} + \frac{1}{2}\overrightarrow{ID}.\overrightarrow{AB} = \overrightarrow{0}.

    Suy ra \overrightarrow{I J}\bot\overrightarrow{AB}. Hay góc giữa cặp vectơ \overrightarrow{AB} và \overrightarrow{IJ} bằng 90^{0}.

  • Câu 15: Vận dụng cao
    Ghi đáp án vào ô trống

    Có ba lực cùng tác động vào một chất điểm. Hai trong ba lực này tạo với nhau một góc 80^{0} và có độ lớn đều bằng 50N, lực còn lại cùng tạo với hai lực kia một góc 60^{0} và có độ lớn bằng 60N. Tính độ lớn của hợp lực của ba lực trên. (Kết quả làm tròn đến hàng đơn vị).

    Đáp án: 124 N

    Đáp án là:

    Có ba lực cùng tác động vào một chất điểm. Hai trong ba lực này tạo với nhau một góc 80^{0} và có độ lớn đều bằng 50N, lực còn lại cùng tạo với hai lực kia một góc 60^{0} và có độ lớn bằng 60N. Tính độ lớn của hợp lực của ba lực trên. (Kết quả làm tròn đến hàng đơn vị).

    Đáp án: 124 N

    Gọi hai lực tạo với nhau một góc 80^{\circ} là \overrightarrow{F_{1}} và \overrightarrow{F_{2}}, ta có \left| \overrightarrow{F_{1}} ight| = \left| \overrightarrow{F_{2}} ight| = 50N.

    Lực còn lại là \overrightarrow{F_{3}}, ta có \left| \overrightarrow{F_{3}} ight| = 60N.

    Gọi \overrightarrow{F} là hợp lực của ba lực trên ta có

    \left| \overrightarrow{F} ight|^{2} = \left( \overrightarrow{F_{1}} + \overrightarrow{F_{2}} + \overrightarrow{F_{3}} ight)^{2}

    = \left| \overrightarrow{F_{1}} ight|^{2} + \left| \overrightarrow{F_{2}} ight|^{2} + \left| \overrightarrow{F_{3}} ight|^{2} + 2\lbrack\left| \overrightarrow{F_{1}} ight|.\left| \overrightarrow{F_{2}} ight|.cos\left( \overrightarrow{F_{1}},\overrightarrow{F_{2}} ight)

    + \left| \overrightarrow{F_{1}} ight|.\left| \overrightarrow{F_{3}} ight|.cos\left( \overrightarrow{F_{1}},\overrightarrow{F_{3}} ight) + \left| \overrightarrow{F_{3}} ight|.\left| \overrightarrow{F_{2}} ight|.cos\left( \overrightarrow{F_{3}},\overrightarrow{F_{2}} ight)brack

    = 50^{2} + 50^{2} + 60^{2} + 2\lbrack 50.50.cos80^{0}+ 50.60.cos60^{0} + 60.50.cos60^{0}brack \approx 15468.

    \Rightarrow |F| \approx 124 N

  • Câu 16: Vận dụng
    Tính góc giữa hai đường thẳng

    Cho hình hộp ABCD.A'B'C'D' có các cạnh đều bằng a và các góc \widehat{B'A'D'} = 60^{0},\widehat{B'A'A} = \widehat{D'A'A} = 120^{0}. Tính góc giữa các cặp đường thẳng AB với A'D; AC' với B'D.

    Hướng dẫn:

    Hình vẽ minh họa

    Đặt \overrightarrow{AA'} = \overrightarrow{a},\overrightarrow{A'B'} = \overrightarrow{b},\overrightarrow{A'D'} = \overrightarrow{c}

    Ta có \overrightarrow{A'D} = \overrightarrow{a} + \overrightarrow{c} nên

    \cos\left( \widehat{AB,A'D} \right) = \left| \cos\left( \overrightarrow{AB},\overrightarrow{A'D} \right) \right|

    = \frac{\left| \overrightarrow{AB}.\overrightarrow{A'D} \right|}{\left| \overrightarrow{AB} \right|\left| \overrightarrow{A'D} \right|} = \frac{\left| \overrightarrow{a}\left( \overrightarrow{a} + \overrightarrow{c} \right) \right|}{\left| \overrightarrow{a} \right|\left| \overrightarrow{a} + \overrightarrow{c} \right|}.

    Để ý rằng \left| \overrightarrow{a} + \overrightarrow{c} \right| = a, \overrightarrow{a}\left( \overrightarrow{a} + \overrightarrow{c} \right) = \frac{a^{2}}{2}.

    Từ đó \cos\left( \widehat{AB,A'D} \right) = \frac{1}{2} \Rightarrow \widehat{(AB,A'D)} = 60^{0}

    Ta có \overrightarrow{AC'} = \overline{b} + \overrightarrow{c} - \overrightarrow{a},\overrightarrow{B'D} = \overrightarrow{a} - \overrightarrow{b} + \overrightarrow{c}, từ đó tính được:

    \overrightarrow{AC'}\overrightarrow{B'D} =\left( \overrightarrow{b} + \overrightarrow{c} - \overrightarrow{a}\right)\left( \overrightarrow{a} - \overrightarrow{b} +\overrightarrow{c} \right) = 0\Rightarrow \widehat{(AC',B'D)} =90^{0}.

  • Câu 17: Thông hiểu
    Tính giá trị biểu thức

    Cho tam giác ABC. Lấy điểm S nằm ngoài mặt phẳng (ABC). Trên đoạn SA lấy điểm M sao cho \overrightarrow{MS} = - 2\overrightarrow{MA} và trên đoạn BC lấy điểm N sao cho \overrightarrow{NB} = - \frac{1}{2}\overrightarrow{NC}. Biết biểu diễn \overrightarrow{MN} = m.\overrightarrow{AB} + n.\overrightarrow{SC} là duy nhất. Tính giá trị biểu thức T = m + n?

    Hướng dẫn:

    Hình vẽ minh họa

    Theo giả thiết ta có: \overrightarrow{MS} = - 2\overrightarrow{MA}; \overrightarrow{NB} = - \frac{1}{2}\overrightarrow{NC}

    Lấy điểm P trên cạnh AC sao cho \overrightarrow{PC} = - 2\overrightarrow{PA}. Khi đó:

    \overrightarrow{MN} = \overrightarrow{MP} + \overrightarrow{PN} = \frac{1}{3}\overrightarrow{SC} + \frac{2}{3}\overrightarrow{AB}

    \Rightarrow \left\{ \begin{matrix}m = \dfrac{2}{3} \ = \dfrac{1}{3} \\\end{matrix} ight.\ \Rightarrow T = 1

  • Câu 18: Vận dụng
    Chọn kết quả đúng nhất

    Cho tam giác ABC, thì công thức tính diện tích nào sau đây là đúng nhất.

    Hướng dẫn:

    Ta có:

    S_{ABC} = \frac{1}{2}ABAC\sin A = \frac{1}{2}\sqrt{AB^{2}AB^{2}sin^{2}A}

    = \frac{1}{2}\sqrt{AB^{2}AC^{2}\left( 1 - cos^{2}A \right)}

    = \frac{1}{2}\sqrt{AB^{2}AC^{2} - \left( \overrightarrow{AB}.\overrightarrow{AC} \right)^{2}}.

  • Câu 19: Vận dụng cao
    Tìm điều kiện của các hệ số a; b; c

    Cho hình chóp S.ABC. Lấy các điểm A';B';C' lần lượt thuộc các tia SA;SB;SC sao cho \frac{SA}{SA'} = a;\frac{SB}{SB'} = b;\frac{SC}{SC'} = c trong đó a;b;c là các hệ số biến thiên. Để mặt phẳng (A'B'C') đi qua trọng tâm của tam giác ABC thì tổng các hệ số bằng bao nhiêu?

    Hướng dẫn:

    Hình vẽ minh họa

    Gọi G là trọng tâm tam giác ABC suy ra \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0}

    Khi đó 3\overrightarrow{GS} + \overrightarrow{SA} + \overrightarrow{SB} + \overrightarrow{SC} = \overrightarrow{0} mà \overrightarrow{SA} = a\overrightarrow{SA'};\overrightarrow{SB} = b\overrightarrow{SB'};\overrightarrow{SC} = c\overrightarrow{SC'}

    Suy ra 3\overrightarrow{SG} = a\overrightarrow{SA'} + b\overrightarrow{SB'} + c\overrightarrow{SC'}

    \Leftrightarrow \overrightarrow{SG} = \frac{a}{3}\overrightarrow{SA'} + \frac{b}{3}\overrightarrow{SB'} + \frac{c}{3}\overrightarrow{SC'}

    Vì mặt phẳng (A'B'C') đi qua trọng tâm của tam giác ABC suy ra \overrightarrow{GA'};\overrightarrow{GB'};\overrightarrow{GC'} đồng phẳng.

    Do đó tồn tại ba số l;m;n sao cho l^{2} + m^{2} + n^{2} eq 0) và l\overrightarrow{GA'} + m\overrightarrow{GB'} + n\overrightarrow{GC'} = \overrightarrow{0}

    \Leftrightarrow l\left( \overrightarrow{GS} + \overrightarrow{SA'} ight) + m\left( \overrightarrow{GS} + \overrightarrow{SB'} ight) + n\left( \overrightarrow{GS} + \overrightarrow{SC'} ight) = \overrightarrow{0}s

    \Leftrightarrow (l + m + n)\overrightarrow{SG} = l\overrightarrow{SA'} + m\overrightarrow{SB'} + n\overrightarrow{SC'}

    \Leftrightarrow \overrightarrow{SG} = \frac{l}{l + m + n}\overrightarrow{SA'} + \frac{m}{l + m + n}\overrightarrow{SB'} + \frac{n}{l + m + n}\overrightarrow{SC'}

    \Leftrightarrow \frac{a}{3}\overrightarrow{SA'} + \frac{b}{3}\overrightarrow{SB'} + \frac{c}{3}\overrightarrow{SC'} = \frac{l}{l + m + n}\overrightarrow{SA'} + \frac{m}{l + m + n}\overrightarrow{SB'} + \frac{n}{l + m + n}\overrightarrow{SC'}

    Suy ra \frac{a}{3} + \frac{b}{3} + \frac{c}{3} = \frac{l}{l + m + n} + \frac{m}{l + m + n} + \frac{n}{l + m + n} = 1

    \Rightarrow a + b + c = 3

  • Câu 20: Vận dụng
    Ghi đáp án vào chỗ trống

    Khi chuyển động trong không gian, máy bay luôn chịu tác động của 4 lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học.

    Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900(km/h) lên 920(km/h), trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900(km/h) và 920(km/h) lần lượt biểu diễn bởi hai vectơ \overrightarrow{F_{1}} và \overrightarrow{F_{2}} với \overrightarrow{F_{1}} =k.\overrightarrow{F_{2}};\left( k\mathbb{\in R};k > 0ight). Tính giá trị của k (Làm tròn kết quả đến chữ số thập phân thứ hai).

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Khi chuyển động trong không gian, máy bay luôn chịu tác động của 4 lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học.

    Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900(km/h) lên 920(km/h), trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900(km/h) và 920(km/h) lần lượt biểu diễn bởi hai vectơ \overrightarrow{F_{1}} và \overrightarrow{F_{2}} với \overrightarrow{F_{1}} =k.\overrightarrow{F_{2}};\left( k\mathbb{\in R};k > 0ight). Tính giá trị của k (Làm tròn kết quả đến chữ số thập phân thứ hai).

    Chỗ nhập nội dung câu trả lời tự luận
0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (20%):
    2/3
  • Thông hiểu (55%):
    2/3
  • Vận dụng (25%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Tải file làm trên giấy
1
74 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này