Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Trắc nghiệm Toán 12 Tọa độ của vectơ (Mức Khó)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Vận dụng
    Chọn đáp án đúng

    Trong không gian Oxyzcho hình hộp chữ nhật OABC.EFGH có các cạnh OA = 5, OC = 8, OE = 7 (xem hình vẽ dưới đây). Tọa độ H(x;y;z). Tính giá trị biểu thức P = 50x + 75y + 1000z

    Hướng dẫn:

    Ta có H \in (yOz) và hình chiếu của H lên Oy trùng với C nên H(0;\ 8;\ 7).

    P = 50x + 75y + 1000z = 50.0 + 75.8 + 1000.7 = 7600.

  • Câu 2: Vận dụng cao
    Tính tổng a, b, c

    Cho tứ diện SABC có ABC là tam giác vuông tại B, BC = 3,\ \ BA = 2,\ \ SA vuông góc với mặt phẳng (ABC) và có độ dài bằng 2. Chọn hệ trục tọa độ như hình bên dưới. Điểm D(a;b;c) sao cho SBCD là hình bình hành. Khi đó a + b + c bằng bao nhiêu?

    Hướng dẫn:

    Các vectơ đơn vị trên các trục Bx,By,Bz lần lượt là \overrightarrow{i},\ \ \overrightarrow{j},\ \ \overrightarrow{k} có độ dài bằng 1.

    Vì \overrightarrow{BA} cùng hướng với \overrightarrow{j} và BA = 2 nên \overrightarrow{BA} = 2\overrightarrow{j}

    Gọi I \in Bz sao cho SABI là hình bình hành, ta có \overrightarrow{BI} cùng hướng với \overrightarrow{k} và BI = SA = 2 nên \overrightarrow{BI} = 3\overrightarrow{k}

    Theo quy tắc hình bình hành, ta có: \overrightarrow{BS} = \overrightarrow{BA} + \overrightarrow{BI} = 2\overrightarrow{j} + 3\overrightarrow{k}

    Vì \overrightarrow{BC} cùng hướng với \overrightarrow{i} và BC = 3 nên \overrightarrow{BC} = 3\overrightarrow{i}

    Gọi \overrightarrow{BD} = a\overrightarrow{i} + b\overrightarrow{j} + c\overrightarrow{k}

    \overrightarrow{CD} =\overrightarrow{BD} - \overrightarrow{BC}= a\overrightarrow{i} +b\overrightarrow{j} + c\overrightarrow{k} - 3\overrightarrow{i}= (a -3)\overrightarrow{i} + b\overrightarrow{j} +c\overrightarrow{k}

    Để SBCD là hình bình hành thì

    \overrightarrow{BS} = \overrightarrow{CD} \Leftrightarrow 2\overrightarrow{j} + 3\overrightarrow{k} = (a - 3)\overrightarrow{i} + b\overrightarrow{j} + c\overrightarrow{k}

    \Leftrightarrow \left\{ \begin{matrix} a - 3 = 0 \\ b = 2 \\ c = 3 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} a = 3 \\ b = 2 \\ c = 3 \\ \end{matrix} \right.

    Vậy a + b + c = 8

  • Câu 3: Vận dụng
    Xác định tính đúng sai của từng phương án

    Trong không gian với hệ trục tọa độ Oxyz, cho \overrightarrow{OA} = 3\overrightarrow{i} - \overrightarrow{k}, với \overrightarrow{i},\overrightarrow{k} là hai vectơ đơn vị trên hai trục tọa độ Ox,Oz, hai điểm B( - 1;2;3),C(1;4;1).

    a) A(3;0; - 1). Đúng||Sai

    b) Ba điểm A,B,C thẳng hàng. Sai||Đúng

    c) Điểm D(a;b;c) là điểm đối xứng của với A qua B. Khi đó a + b + c = 6. Đúng||Sai

    d) Điểm M(m;n;p) trên mặt phẳng (Oxy) sao cho MA^{2} + MB^{2} + MC^{2} đạt giá trị nhỏ nhất. Khi đó 2m - n + 2024p = 0. Đúng||Sai

    Đáp án là:

    Trong không gian với hệ trục tọa độ Oxyz, cho \overrightarrow{OA} = 3\overrightarrow{i} - \overrightarrow{k}, với \overrightarrow{i},\overrightarrow{k} là hai vectơ đơn vị trên hai trục tọa độ Ox,Oz, hai điểm B( - 1;2;3),C(1;4;1).

    a) A(3;0; - 1). Đúng||Sai

    b) Ba điểm A,B,C thẳng hàng. Sai||Đúng

    c) Điểm D(a;b;c) là điểm đối xứng của với A qua B. Khi đó a + b + c = 6. Đúng||Sai

    d) Điểm M(m;n;p) trên mặt phẳng (Oxy) sao cho MA^{2} + MB^{2} + MC^{2} đạt giá trị nhỏ nhất. Khi đó 2m - n + 2024p = 0. Đúng||Sai

    a) Đúng: Vì \overrightarrow{OA} = 3\overrightarrow{i} - \overrightarrow{k} nên A(3;0; - 1).

    b) Sai: Ta có \overrightarrow{AB} = (4;2;4),\overrightarrow{AC} = ( - 2;4;2).

    Vì 4:2:4 eq - 2:4:2 nên \overrightarrow{AB},\overrightarrow{AC} không cùng phương suy ra A,B,C không thẳng hàng.

    c) Đúng

    Vì D là điểm đối xứng với A qua B nên B là trung điểm của AD.

    Ta có \left\{ \begin{matrix} x_{D} = 2x_{B} - x_{A} = - 5 \\ y_{D} = 2y_{B} - y_{A} = 4 \\ z_{D} = 2z_{B} - z_{A} = 7. \\ \end{matrix} ight. suy ra D( - 5;4;7).

    Do đó a = - 5,b = 4,c = 7. Vậy a + b + c = 6.

    d) Đúng. Gọi I(x;y;z) là điểm thỏa mãn \overrightarrow{IA} + \overrightarrow{IB} + \overrightarrow{IC} = \overrightarrow{0}.

    Ta có:

    \left\{ \begin{matrix} 3 - x - 1 - x + 1 - x = 0 \\ 0 - y + 2 - y + 4 - y = 0 \\ - 1 - z + 3 - z + 1 - z = 0 \\ \end{matrix} ight.\Leftrightarrow \left\{ \begin{matrix} x = 1 \\ y = 2 \\ z = 1 \\ \end{matrix} \Rightarrow I(1;2;1) ight.

    MA^{2} + MB^{2} + MC^{2}

    =(\overrightarrow{MI} + \overrightarrow{IA})^{2} + (\overrightarrow{MI} +\overrightarrow{IB})^{2} + (\overrightarrow{MI} +\overrightarrow{IC})^{2}

    = 3MI^{2} + IA^{2} + IB^{2} + IC^{2} +2\overrightarrow{MI}(\overrightarrow{IA} + \overrightarrow{IB} +\overrightarrow{IC})

    = 3MI^{2} + IA^{2} + IB^{2} + IC^{2}

    Do IA^{2} + IB^{2} + IC^{2} không thay đổi nên MA^{2} + MB^{2} + MC^{2} nhỏ nhất khi MI nhỏ nhất hay M là hình chiếu của điểm I trên mặt phẳng (Oxy).

    Do đó M(1;2;0) suy ra m=1,n=2,p=0.

    Vậy 2m - n + 2024p = 2 - 2 + 0 = 0.

  • Câu 4: Vận dụng
    Tính giá trị biểu thức

    Trong không gian với hệ trục Oxyz cho ba điểm A( - 1;2; - 3),\ \ B(1;0;2),\ \ C(x;y; - 2) thẳng hàng. Khi đó x + y bằng

    Hướng dẫn:

    Có \overrightarrow{AB} = (2; - 2;5),\ \ \overrightarrow{AC} = (x + 1;y - 2;1).

    A,\ B,\ C thẳng hàng \Leftrightarrow \overrightarrow{AB},\overrightarrow{AC} cùng phương

    \Leftrightarrow \frac{x + 1}{2} = \frac{y - 2}{- 2} = \frac{1}{5}

    \Leftrightarrow \left\{ \begin{matrix} x = - \dfrac{3}{5} \\ y = \dfrac{8}{5} \\ \end{matrix} ight.\ \Rightarrow x + y = 1.

  • Câu 5: Vận dụng
    Xác định tính đúng sai của từng phương án

    Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;3),B(2;1;5),C(2;4;2). Xét tính đúng sai của các khẳng định sau:

    a) Tọa độ trung điểm của AB là \left( \frac{3}{2};\frac{3}{2};4 ight). Đúng||Sai

    b) \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = (5;7;10). Đúng||Sai

    c) Góc giữa hai đường thẳng AB và AC bằng 30^{\circ}. Đúng||Sai

    d) Điểm I(a;b;c) nằm trên mặt phẳng (Oxz) thỏa mãn T = |3\overrightarrow{IB} - \overrightarrow{IC}| đạt giá trị nhỏ nhất. Khi đó a - 2b + 2c = 15. Sai||Đúng

    Đáp án là:

    Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;3),B(2;1;5),C(2;4;2). Xét tính đúng sai của các khẳng định sau:

    a) Tọa độ trung điểm của AB là \left( \frac{3}{2};\frac{3}{2};4 ight). Đúng||Sai

    b) \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = (5;7;10). Đúng||Sai

    c) Góc giữa hai đường thẳng AB và AC bằng 30^{\circ}. Đúng||Sai

    d) Điểm I(a;b;c) nằm trên mặt phẳng (Oxz) thỏa mãn T = |3\overrightarrow{IB} - \overrightarrow{IC}| đạt giá trị nhỏ nhất. Khi đó a - 2b + 2c = 15. Sai||Đúng

    a) Đúng: Gọi I là trung điểm AB.

    Ta có \left\{ \begin{matrix} {x_I} = \dfrac{{{x_A} + {x_B}}}{2} = \dfrac{{1 + 2}}{2} = \dfrac{3}{2} \hfill \\ {y_I} = \dfrac{{{y_A} + {y_B}}}{2} = \dfrac{{2 + 1}}{2} = \dfrac{3}{2} \hfill \\ {z_I} = \dfrac{{{z_A} + {z_B}}}{2} = \dfrac{{3 + 5}}{2} = 4 \hfill \\ \end{matrix} ight. \Rightarrow I\left( {\dfrac{3}{2};\dfrac{3}{2};4} ight)

    b) Đúng: Ta có \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = (5;7;10).

    c) Đúng: Ta có \overrightarrow{AB} = (1; - 1;2),\overrightarrow{AC} = (1;2; - 1).

    \cos(AB,AC) =\cos(\overrightarrow{AB},\overrightarrow{AC}) =\frac{|\overrightarrow{AB} \cdot\overrightarrow{AC}|}{|\overrightarrow{AB}| \cdot|\overrightarrow{AC}|}

    = \frac{|1 \cdot 1 + ( - 1) \cdot 2 + 2 \cdot ( - 1)|}{\sqrt{1^{2} + ( - 1)^{2} + 2^{2}} \cdot \sqrt{1^{2} + 2^{2} + ( - 1)^{2}}} = \frac{1}{2}

    Suy ra (AB,AC) = 60^{\circ}.

    d) Sai: Gọi K(x;y;z) thỏa mãn 3\overrightarrow{KB} - \overrightarrow{KC} = \overrightarrow{0}

    \Leftrightarrow \left\{ \begin{matrix}3(2 - x) - (2 - x) = 0 \\3(1 - y) - (4 - y) = 0 \\3(5 - z) - (2 - z) = 0 \\\end{matrix} \Leftrightarrow \left\{ \begin{matrix}x = 2 \\y = - \dfrac{1}{2} \\z = \dfrac{13}{2} \\\end{matrix} ight.\ ight.

    Suy ra K\left( 2; - \frac{1}{2};\frac{13}{2} ight).

    Khi đó T = |3\overrightarrow{IB} - \overrightarrow{IC}| = |3\overrightarrow{IK} + 3\overrightarrow{KB} - \overrightarrow{IK} - \overrightarrow{KC}| = |2\overrightarrow{IK}| = 2IK.

    T đạt giá trị nhỏ nhất khi và chỉ khi I là hình chiếu của K trên (Oxz) suy ra I(2;0;\frac{13}{2} )..

    Suy ra a = 2,b = 0,c = \frac{13}{2}.

    Vậy a - 2b + 2c = 15.

  • Câu 6: Vận dụng cao
    Tính giá trị biểu thức

    Trong không gian Oxyz, cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 5 , giao điểm hai đường chéo AC và BD trùng với gốc O. Các vectơ \overrightarrow{OB},\ \ \overrightarrow{OC},\ \ \overrightarrow{OS} lần lượt cùng hướng với \overrightarrow{i}, \overrightarrow{j},\overrightarrow{k} và OA = OS = 4 như hình bên dưới. Toạ độ vectơ \overrightarrow{AM} = (a;b;c) với M là trung điểm của cạnh SC, khi đó a + b + c bằng bao nhiêu?

    Hướng dẫn:

    Vì ABCD là hình thoi cạnh bằng 5 , O là giao điểm của AC và BD nên O là trung điểm của AC và BD.

    Xét \Delta OAB vuông tại O, có OB = \sqrt{AB^{2} - OA^{2}} = \sqrt{25 - 16} = 3.

    Vì \overrightarrow{OB} và \overrightarrow{i} cùng hướng và OB = 3 nên \overrightarrow{OB} = 3\overrightarrow{i}.

    Vì \overrightarrow{OA} và \overrightarrow{j} cùng hướng và OA = 4 nên \overrightarrow{OA} = - 4\overrightarrow{j}.

    Ta có \overrightarrow{AB} = \overrightarrow{OB} - \overrightarrow{OA} = 3\overrightarrow{i} + 4\overrightarrow{j}

    Có AC = 2OA = 8 mà \overrightarrow{AC} và \overrightarrow{j} cùng hướng nên \overrightarrow{AC} = 8\overrightarrow{j}.

    Có \overrightarrow{OS} và \overrightarrow{k} cùng hướng và OS = 4 nên \overrightarrow{OS} = 4\overrightarrow{k}.

    Có \overrightarrow{SB} = \overrightarrow{OB} - \overrightarrow{OS} = 3\overrightarrow{i} - 4\overrightarrow{k}

    Lại có \overrightarrow{AS} = \overrightarrow{AB} + \overrightarrow{BS} = \left( 3\overrightarrow{i} + 4\overrightarrow{j} \right) - \left( 3\overrightarrow{i} - 4\overrightarrow{k} \right) = 4\overrightarrow{j} + 4\overrightarrow{k}.

    Vì M là trung điểm của SC nên \overrightarrow{AM} = \frac{1}{2}\left( \overrightarrow{AS} + \overrightarrow{AC} \right) = \frac{1}{2}\left( 4\overrightarrow{j} + 4\overrightarrow{k} + 8\overrightarrow{j} \right) = 6\overrightarrow{j} + 2\overrightarrow{k}.

    Do đó \overrightarrow{AM} = (0;6;2).

    Suy ra a + b + c = 0 + 6 + 2 = 8

  • Câu 7: Vận dụng cao
    Chọn phương án đúng

    Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2,\ \ SA vuông góc với đáy và SA bằng 1. Thiết lập hệ tọa độ như hình vẽ bên dưới, tọa độ điểm S\left( a;\sqrt{b};c \right). Khi đó a + b + c bằng bao nhiêu?

    Hướng dẫn:

    Các vectơ đơn vị trên các trục Ox,Oy,Oz lần lươt là \overrightarrow{i} = \overrightarrow{OC},\ \ \overrightarrow{j} = \overrightarrow{OE},\ \ \overrightarrow{k} = \overrightarrow{OH} với E là điểm thuộc tia Oy sao cho OE = 1 và H là điểm thuộc tia Oz sao cho OH = 1.

    Vì \Delta ABC đều và AO\bot BC nên O là trung điểm cùa BC.

    Mà BC = 2 nên OB = OC = 1 và OA = \sqrt{3}.

    Vì \overrightarrow{OA} và \overrightarrow{j} cùng hướng và OA = \sqrt{3} nên \overrightarrow{OA} = \sqrt{3}\overrightarrow{j}.

    Theo quy tắc hình bình hành, ta có \overrightarrow{OS} = \overrightarrow{OA} + \overrightarrow{OH} = \sqrt{3}\overrightarrow{j} + \overrightarrow{k}.

    Suy ra S\left( 0;\sqrt{3};1 \right). Vậy a + b + c = 0 + 3 + 1 = 4

  • Câu 8: Vận dụng
    Xác định tính đúng sai của các nhận định

    Trong không gian Oxyz, cho hình bình hành OABC với A(1;\ 2;\ 3), B(5;\ 0;\ - 1), và C(a;b;c)

    a. Tọa độ điểm O(0;0;1).Sai||Đúng

    b. Tọa độ vectơ \overrightarrow{OA} = (1;\ 2;\ 3). Đúng||Sai

    c. \overrightarrow{OB} = 5.\overrightarrow{i} - \overrightarrow{k}. Đúng||Sai

    d. Nếu OABC hình bình hành, thì a + b + c = 2. Đúng||Sai

    Đáp án là:

    Trong không gian Oxyz, cho hình bình hành OABC với A(1;\ 2;\ 3), B(5;\ 0;\ - 1), và C(a;b;c)

    a. Tọa độ điểm O(0;0;1).Sai||Đúng

    b. Tọa độ vectơ \overrightarrow{OA} = (1;\ 2;\ 3). Đúng||Sai

    c. \overrightarrow{OB} = 5.\overrightarrow{i} - \overrightarrow{k}. Đúng||Sai

    d. Nếu OABC hình bình hành, thì a + b + c = 2. Đúng||Sai

    (a) Tọa độ điểm O(0;0;1).

    Trong không gian Oxyz, gốc tọa độ O(0;0;0).

    » Chọn SAI.

    (b) Tọa độ vectơ \overrightarrow{OA} = (1;\ 2;\ 3).

    Điểm A(1;\ 2;\ 3), suy ra \overrightarrow{OA} = 1.\overrightarrow{i} + 2.\overrightarrow{j} + 3.\overrightarrow{k} = (1;\ 2;\ 3) .

    » Chọn ĐÚNG.

    (c) \overrightarrow{OB} = 5.\overrightarrow{i} - \overrightarrow{k}.

    Ta có B(5;\ 0;\ - 1). Suy ra vectơ \overrightarrow{OB} = 5.\overrightarrow{i} - 1.\overrightarrow{k}.

    » Chọn ĐÚNG.

    (d) Nếu OABC hình bình hành, thì a + b + c = 2.

    Ta có \overrightarrow{OA} = 1.\overrightarrow{i} + 2.\overrightarrow{j} + 3.\overrightarrow{k} = (1;\ 2;\ 3), C(a;b;c)

    \Rightarrow \overrightarrow{OC} = a\overrightarrow{i} + b\overrightarrow{j} + c\overrightarrow{k}\overrightarrow{CB} = \overrightarrow{OB} - \overrightarrow{OC}

    = \left( 5.\overrightarrow{i} -1.\overrightarrow{k} \right) - \left( a.\overrightarrow{i} +b.\overrightarrow{j} + c.\overrightarrow{k} \right)= (5 - a;b; - 1 -c).

    OABC hình bình hành, thì \left\{ \begin{matrix} 5 - a = 1 \\ b = 2 \\ - 1 - c = 3 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} a = 4 \\ b = 2 \\ c = - 4 \\ \end{matrix} \right.. Khi đó a + b + c = 2.

    » Chọn ĐÚNG.

  • Câu 9: Vận dụng
    Xác định tọa độ điểm C’

    Trong không gian hệ trục tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có tọa độ các điểm A( - 3;0;0),B(0;2;0),D(0;0;1),A'(1;2;3). Tìm tọa độ điểm C'?

    Hướng dẫn:

    Theo quy tắc hình hộp ta có:

    \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA'} = \overrightarrow{AC'}

    Lại có \left\{ \begin{matrix} \overrightarrow{AB} = (3;2;0) = 3\overrightarrow{i} + 2\overrightarrow{j} + 0.\overrightarrow{k} \\ \overrightarrow{AD} = (3;0;1) = 3.\overrightarrow{i} + 0.\overrightarrow{j} + 1.\overrightarrow{k} \\ \overrightarrow{AA'} = (4;2;3) = 4.\overrightarrow{i} + 2\overrightarrow{j} + 3\overrightarrow{k} \\ \end{matrix} ight.

    \Rightarrow \overrightarrow{AC'} = 10.\overrightarrow{i} + 4.\overrightarrow{j} + 4.\overrightarrow{k} mà A( - 3;0;0)

    \Rightarrow C'(7;4;4)

    Suy ra C'(7;4;4)

  • Câu 10: Thông hiểu
    Tìm tọa độ điểm D thỏa mãn yêu cầu

    Trong không gian hệ trục tọa độ Oxyz, cho các điểm A(1;0;1),B(2;1; - 2),C( - 1;3;2). Biết rằng tứ giác ABCD là hình bình hành, khi đó tọa độ điểm D là:

    Hướng dẫn:

    Giả sử điểm D(x;y;z) ta có ABCD là hình bình hành nên \overrightarrow{BA} = \overrightarrow{CD}

    \Leftrightarrow \left\{ \begin{matrix} x + 1 = - 1 \\ y - 3 = - 1 \\ z - 2 = 3 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = - 2 \\ y = 2 \\ z = 5 \\ \end{matrix} ight.. Vậy tọa độ điểm D( - 2;2;5)

  • Câu 11: Thông hiểu
    Tìm tọa độ điểm B

    Trong không gian với hệ trục tọa độ Oxyz, cho  A(1;2; - 1);\overrightarrow{AB} =(1;3;1), khi đó tọa độ điểm B là:

    Hướng dẫn:

    Gọi B(x;y;z) ta có:

    A(1;2; - 1);\overrightarrow{AB} =(1;3;1) khi đó \left\{\begin{matrix}x - 1 = 1 \\y - 2 = 3 \\z + 1 = 1 \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}x = 2 \\y = 5 \\z = 0 \\\end{matrix} ight. nên tọa độ điểm cần tìm là B(2;5;0).

  • Câu 12: Vận dụng cao
    Xác định giá trị của biểu thức

    Trong không gian Oxyz cho A(1;0;2), B( - 1;2;2), C(3;1;1). Gọi M(a;b;c) là điểm thuộc mặt phẳng (Oxz) sao cho biểu thức S = 2\overrightarrow{MA}.\overrightarrow{MB} + \overrightarrow{MB}.\overrightarrow{MC} + 3\overrightarrow{MC}.\overrightarrow{MA} đạt giá trị nhỏ nhất. Khi đó T = 6a - 5b + 3c có giá trị là

    Hướng dẫn:

    Do M(a;b;c) thuộc mặt phẳng (Oxz) nên b = 0 \Rightarrow M(a;0;c).

    Ta có \overrightarrow{MA} = (1 - a;0;2 - c), \overrightarrow{MB} = ( - 1 - a;2;2 - c), \overrightarrow{MC} = (3 - a;1;1 - c).

    S = 2\overrightarrow{MA}.\overrightarrow{MB} + \overrightarrow{MB}.\overrightarrow{MC} + 3\overrightarrow{MC}.\overrightarrow{MA}

    = 2\left( a^{2} - 1 + 4 - 4c + c^{2}\right)+ \left( a^{2} - 2a - 3 + 2 + c^{2} - 3c + 2 \right)+ 3\left(a^{2} - 4a + 3 + c^{2} - 3c + 2 \right)= 6a^{2} + 6c^{2} - 14a - 20c + 22

    = 6\left( a - \frac{7}{6} \right)^{2} + 6\left( b - \frac{5}{3} \right)^{2} - \frac{17}{6} \geq - \frac{17}{6}.

    Suy ra S đạt giá trị nhỏ nhất - \frac{17}{6} khi và chỉ khi \left\{ \begin{matrix} a = \frac{7}{6} \\ c = \frac{5}{3} \\ \end{matrix} \right..

    Vậy T = 6a - 5b + 3c = 6.\frac{7}{6} - 5.0 + 3.\frac{5}{3} = 12.

  • Câu 13: Vận dụng
    Xác định toạ độ của vectơ biểu diễn độ dịch chuyển

    Để theo dõi hành trình của một chiếc máy bay, ta có thể lập hệ toạ độ Oxyz có gốc O trùng với vị trí của trung tâm kiểm soát không lưu, mặt phẳng (Oxy) trùng với mặt đất với trục Ox hướng về phía tây, trục Oy hướng về phía nam và trục Oz hướng thẳng đứng lên trời. Sau khi cất cánh và đạt độ cao nhất định, chiếc máy bay duy trì hướng bay về phía nam với tốc độ không đổi là 890\ km/h trong nửa giờ. Xác định toạ độ của vectơ biểu diễn độ dịch chuyển của chiếc máy bay trong nửa giờ đó đối với hệ toạ độ đã chọn, biết rằng đơn vị đo trong không gian Oxyzđược lấy theo kilômét.

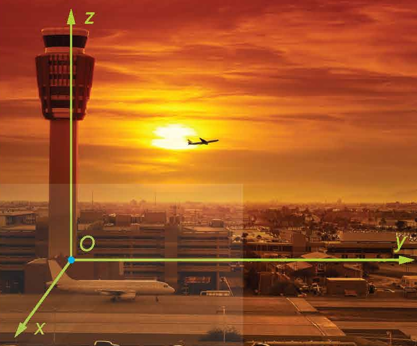
    A sunset over a cityDescription automatically generated with medium confidence

    Hướng dẫn:

    Quãng đường máy bay bay được với vận tốc 890km/h trong nửa giờ là:

    890.\frac{1}{2} = 445(km)

    Vì máy bay duy trì hướng bay về phía nam nên tọa độ của vectơ biểu diễn độ dịch chuyển của chiếc máy bay trong nửa giờ đó với hệ tọa độ đã chọn là (0;445;0).

  • Câu 14: Vận dụng cao
    Xác định tọa độ của máy bay

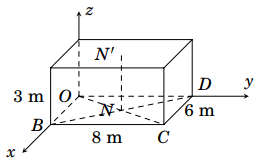
    Trong không gian với một hệ trục toạ độ cho trước, ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm A(800;500;7) đến điểm B(940;550;8) trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 5 phút tiếp theo là gì?

    A drawing of a point of a personDescription automatically generated with medium confidence

    Hướng dẫn:

    Gọi D(x;y;z) là vị trí của máy bay sau 5 phút tiếp theo. Vì hướng của máy bay không đổi nên \overrightarrow{AB} và \overrightarrow{BD} cùng hướng. Do vận tốc của máy bay không đổi và thời gian bay từ A đến B gấp đôi thời gian bay từ B đến D nên AB = 2BD.

    Do đó \overrightarrow{BD} = \frac{1}{2}\overrightarrow{AB} = (70;25;0,5).

    Mặt khác, \overrightarrow{BD} = (x - 940;y - 550;z - 8) nên \left\{ \begin{matrix} x - 940 = 70 \\ y - 550 = 25 \\ z - 8 = 0,5 \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = 1010 \\ y = 575 \\ z = 8,5 \\ \end{matrix} \right.\ \Rightarrow D(1010;575;8,5).

    Vậy tọa độ của máy bay sau 5 phút tiếp theo là (1\ \ 010;575;8,5).

  • Câu 15: Thông hiểu
    Ghi đáp án vào ô trống

    Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A( - 1; - 1;3), B(0;2;0) và C(5; - 2;1). Điểm D(a;b;c) sao cho tứ giác ABCD là hình bình hành. Tính S = a + b + c?

    Đáp án: 3

    Đáp án là:

    Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A( - 1; - 1;3), B(0;2;0) và C(5; - 2;1). Điểm D(a;b;c) sao cho tứ giác ABCD là hình bình hành. Tính S = a + b + c?

    Đáp án: 3

    Gọi D = (x;y;z) \Rightarrow \overrightarrow{DC} = (5 - x; - 2 - y;1 - z)

    Ta có: \overrightarrow{AB} = (1;3; - 3)

    ABCD là hình bình hành nên \overrightarrow{AB} = \overrightarrow{DC}

    \Rightarrow \left\{ \begin{matrix} 5 - x = 1 \\ - 2 - y = 3 \\ 1 - z = - 3 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x = 4 \\ y = - 5 \\ z = 4 \\ \end{matrix} ight.\ \Rightarrow D(4; - 5;4).

    Vậy S = a + b + c = 3.

  • Câu 16: Thông hiểu
    Tìm tọa độ điểm P

    Trong không gian Oxyz, cho hai điểm M(2;1;2), N(4; 2; 1), tọa độ điểm P thuộc trục Oz sao cho M;N; Pthẳng hàng là

    Hướng dẫn:

    Vì điểm Pthuộc trục Oz nên P có tọa độ P(0;0;z).

    Ta có \overrightarrow{MN}(2;1; - 1); \overrightarrow{NP}( - 4; - 2;z - 1)

    M;\ N;\ P thẳng hàng\Leftrightarrow\overrightarrow{MN};\overrightarrow{NP} cùng phương

    \Leftrightarrow \frac{- 4}{2} = \frac{- 2}{1} = \frac{z - 1}{- 1} \Leftrightarrow z - 1 = 2 \Leftrightarrow z = 3

    Vậy điểm P(0;0;3).

  • Câu 17: Vận dụng
    Chọn đáp án đúng

    Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2;3) và B(5;0;1). Điểm M thỏa mãn MA.\overrightarrow{MA} = - 4MB.\overrightarrow{MB} có tọa độ là:

    Hướng dẫn:

    Từ giả thiết MA.\overrightarrow{MA} = - 4MB.\overrightarrow{MB} \Rightarrow \overrightarrow{MA} = - 4\frac{MB}{MA}.\overrightarrow{MB} nên ba điểm M;B;A thẳng hàng và A;B nằm khác phía so với điểm M do - 4\frac{MB}{MA} âm.

    Lại có MA.\overrightarrow{MA} = - 4MB.\overrightarrow{MB}

    \Rightarrow \left( MA.\overrightarrow{MA} \right)^{2} = \left( 4MB.\overrightarrow{MB} \right)^{2}

    \Rightarrow MA^{4} = 16MB^{4} \Rightarrow MA = 2MB.

    \Rightarrow \overrightarrow{MA} = - 2\overrightarrow{MB}.

    Gọi tọa độ M(x;y;z), khi đó

    \left\{ \begin{matrix} 1 - x = - 2(5 - x) \\ 2 - y = - 2(0 - y) \\ 3 - z = - 2(1 - z) \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x = \frac{11}{3} \\ y = \frac{2}{3} \\ z = \frac{5}{3} \\ \end{matrix} \right.

  • Câu 18: Vận dụng
    Chọn khẳng định đúng

    Trong không gian hệ trục tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có tọa độ các điểm A(1;0;1),B(2;1;2),D(1; - 1;1),C'(4;5; - 5). Tìm tọa độ điểm A'?

    Hướng dẫn:

    Theo quy tắc hình hộp ta có:

    \overrightarrow{AB} + \overrightarrow{AD} + \overrightarrow{AA'} = \overrightarrow{AC'}

    \Rightarrow \overrightarrow{AA'} = \overrightarrow{AB} - \overrightarrow{AD} - \overrightarrow{AC'}

    Lại có \left\{ \begin{matrix} \overrightarrow{AB} = (1;1;1) = \overrightarrow{i} + \overrightarrow{j} + \overrightarrow{k} \\ \overrightarrow{AD} = (0; - 1;0) = 0.\overrightarrow{i} - \overrightarrow{j} + 0.\overrightarrow{k} \\ \overrightarrow{AC'} = (3;5; - 6) = 3.\overrightarrow{i} + 5\overrightarrow{j} - 6\overrightarrow{k} \\ \end{matrix} ight. do đó \Rightarrow \overrightarrow{AA'} = 2\overrightarrow{i} + 5\overrightarrow{j} - 6\overrightarrow{k} hay \overrightarrow{AA'} = (3;5; - 6)

    Suy ra A'(3;5; - 6)

  • Câu 19: Vận dụng
    Tìm tọa độ điểm C’

    Trong không gian hệ trục tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có tọa độ các điểm A( -3;0;0),B(0;2;0),D(0;0;1),A'(1;2;3). Giả sử điểm C'(a;b;c). Tính giá trị biểu thức T=a+b+2c?

    Hướng dẫn:

    Gọi điểm C'(x;y;z)

    Ta có: \left\{ \begin{matrix}\overrightarrow{AB} = (3;2;0) = 3\overrightarrow{i} +2\overrightarrow{j} + 0.\overrightarrow{k} \\\overrightarrow{AD} = (3;0;1) = 3.\overrightarrow{i} +0.\overrightarrow{j} + 1.\overrightarrow{k} \\\overrightarrow{AA'} = (4;2;3) = 4.\overrightarrow{i} +2\overrightarrow{j} + 3\overrightarrow{k} \\\end{matrix} ight.

    Mà \overrightarrow{AB} +\overrightarrow{AD} + \overrightarrow{AA'} =\overrightarrow{AC'} \Rightarrow \overrightarrow{AC'} =10\overrightarrow{i} + 4\overrightarrow{j} +4\overrightarrow{k}

    Suy ra \left\{ \begin{matrix}x = 10 + 3 \\y = 4 - 0 \\z = 4 - 0 \\\end{matrix} ight.\ \Rightarrow C'(13;4;4) suy ra a=13;b=4;c=4

    Vậy  T=25

  • Câu 20: Vận dụng cao
    Tìm tọa độ của máy bay theo yêu cầu

    Máy bay chiến đấu của Nga di chuyển với vận tốc và hướng không đổi từ điểm M(600;400;20)đến điểm N(800;500;30) trong 30 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì tọa độ của máy bay sau 15 phút tiếp theo bằng bao nhiêu?

    1

    Hướng dẫn:

    Gọi Q(x;y;z) là tọa độ của máy bay sau 15 phút tiếp theo.

    \overrightarrow{MN} = (200;100;10)

    \overrightarrow{NQ} = (x - 800;y - 500;z - 30)

    Vì máy bay giữ nguyên hướng bay nên \overrightarrow{MN} và \overrightarrow{NQ} cùng hướng.

    Do máy bay tiếp tục giữ nguyên vận tốc và thời gian bay từ M \rightarrow N gấp 2 lần thời gian bay từ N \rightarrow Q nên MN = 2NQ

    Suy ra \overrightarrow{MN} =2\overrightarrow{NQ} \Leftrightarrow \left\{ \begin{matrix}200 = 2(x - 800) \\100 = 2(y - 500) \\10 = 2(z - 30) \\\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}x = 900 \\y = 550 \\z = 35 \\\end{matrix} \right.\ \Rightarrow Q(900;550;35)

    Tọa độ của máy bay sau 15 phút tiếp theo là (900;550;35)

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (20%):
    2/3
  • Thông hiểu (50%):
    2/3
  • Vận dụng (30%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
1
18 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Lớp 12
Xem thêm