Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Trắc nghiệm Toán 12 Phương trình mặt cầu CTST (Mức Khó)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Vận dụng cao
    Viết phương trình đường thẳng

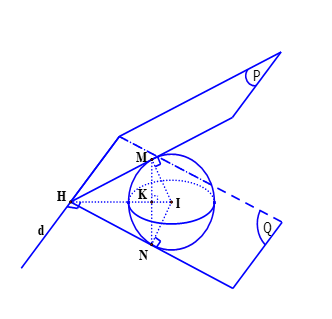
    Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:\frac{x - 13}{- 1} = \frac{y + 1}{1} = \frac{z}{4} và mặt cầu (S):x^{2} + y^{2} + z^{2} - 2x - 4y - 6z - 67 = 0. Qua d dựng các mặt phẳng tiếp xúc với (S) lần lượt tại T_{1};T_{2}. Viết phương trình đường thẳng T_{1}T_{2}.

    Hướng dẫn:

    Ta có mặt cầu (S) có tâm I(1;2;3), bán kính R = 3.

    Đường thẳng d đi qua điểm A(13; - 1;0), có vectơ chỉ phương \overrightarrow{u}( - 1;1;4).

    Mặt phẳng (P) chứa d có dạng (P):A(x - 13) + B(y + 1) + Cz = 0 ,\left( A^{2} + B^{2} + C^{2} \neq 0 \right)

    Do d \subset (P) nên ta có - 1.A + 1.B + 4.C = 0 \Leftrightarrow B = A - 4C.

    Ta có điều kiện tiếp xúc: R = d\left( I;(P) \right) \Leftrightarrow 9 = \frac{| - 12A + 3B + 3C|}{\sqrt{A^{2} + B^{2} + C^{2}}}

    \Leftrightarrow 9 = \frac{|9A + 9C|}{\sqrt{2A^{2} + 17B^{2} - 8AC^{2}}} \Leftrightarrow \left\lbrack \begin{matrix} A = 2C \\ A = 8C \end{matrix} \right.

    Suy ra hai mặt phẳng tiếp diện là \left( P_{1} \right):2x - 2y + z - 28 = 0, \left( P_{2} \right):8x + 4y + z - 100 = 0.

    Suy ra tọa độ các tiếp điểm T_{1}(7; - 4;6),T_{2}(9;6;4) \Rightarrow T_{1}T_{2}:\frac{x - 7}{1} = \frac{y + 4}{5} = \frac{z - 6}{- 1}

  • Câu 2: Thông hiểu
    Chọn phương án đúng

    Tìm tập hợp các tâm I của mặt cầu

    (S):x^{2} + y^{2} + z^{2} + 2(1 - m)x +2(3 - 2m)y + 2(m - 2)z + 5m^{2} - 9m + 6 = 0

    Hướng dẫn:

    Ta có: a = m - 1;\ \ b = 2m - 3;\ \ c = 2 - m;\ \ d = 5m^{2} - 9m + 6

    Tâm I(x = m - 1;y = 2m - 3;z = 2 - m)

    \Rightarrow x + 1 = \frac{y + 3}{2} = 2 - z

    (S) là mặt cầu \Leftrightarrow (m - 1)^{2} + (2m - 3)^{2} + (2 - m)^{2} - 5m^{2} + 9m - 6 > 0

    \Leftrightarrow m^{2} - 9m + 8 > 0 \Leftrightarrow \left\lbrack \begin{matrix} m < 1 \\ m > 8 \\ \end{matrix} \right.

    \Leftrightarrow \left\lbrack \begin{matrix} m - 1 < 0 \\ m - 1 > 7 \\ \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} x < 0 \\ x > 7 \\ \end{matrix} \right.

    Vậy tập hợp các điểm I là phân đường thẳng x + 1 = \frac{y + 3}{2} = 2 - z tương ứng với \left\lbrack \begin{matrix} x < 0 \\ x > 7 \\ \end{matrix} \right..

  • Câu 3: Thông hiểu
    Chọn các đáp án đúng

    Người ta định nghĩa mặt cầu (S) như sau, hãy chọn câu trả lời đúng. (Có thể chọn nhiều đáp án)

    Hướng dẫn:

    Tất cả các đáp án đã cho đều đúng.

  • Câu 4: Vận dụng cao
    Tính độ dài đoạn thẳng MN

    Trong không gian với hệ trục tọa độ Oxyzcho đường thẳng d:\frac{x - 2}{2} = \frac{y}{- 1} = \frac{z}{4} và mặt cầu (S):(x - 1)^{2} + (y - 2)^{2} + (z - 1)^{2} = 2. Hai mặt phẳng (P) và (Q) chứa d và tiếp xúc với (S). Gọi M và N là tiếp điểm. Độ dài đoạn thẳng MN bằng

    Hướng dẫn:

    Hình vẽ minh họa

    Từ (S) Tâm I(1;2;1) và bán kính R = \sqrt{2}

    Từ d Vectơ \overrightarrow{u} = (2; - 1;4)

    Hạ \overrightarrow{u} = (2; - 1;4) \Rightarrow H(2 + 2t; - t;4t)

    \Rightarrow \overrightarrow{IH}.\overrightarrow{u} = \overrightarrow{0}

    \Leftrightarrow (2t + 1).2 + ( - 1).( - 2 - t) + (4t - 1).4 = 0

    \Leftrightarrow t = 0 \Leftrightarrow H(2;0;0)

    Xét tam giác \Delta IHM vuông tại M ta có:

    MH^{2} = IH^{2} - IM^{2} = 62 = 4 \Rightarrow MH = 2.

    Ta có \frac{1}{MK^{2}} = \frac{1}{MH^{2}} + \frac{1}{MI^{2}} = \frac{1}{4} + \frac{1}{2} = \frac{3}{4} \Rightarrow MK = \frac{2}{\sqrt{3}}.

    \Rightarrow MN = 2MK = \frac{4}{\sqrt{3}}.

  • Câu 5: Thông hiểu
    Tính đường kính của mặt cầu

    Cho các điểm A(2;4; - 1) và B(0; - 2;1) và đường thẳng d:\left\{ \begin{matrix} x = 1 + 2t \\ y = 2 - t \\ z = 1 + t \\ \end{matrix} \right.. Gọi (S) là mặt cầu đi qua A, B và có tâm thuộc đường thẳng d. Đường kính mặt cầu (S) bằng:

    Hướng dẫn:

    Gọi I(1 + 2t;2 - t;1 + t) trên d vì IA = IB \Rightarrow t = 1 \Rightarrow R = IA = \sqrt{19} đường kính là 2\sqrt{19}.

  • Câu 6: Vận dụng cao
    Chọn đáp án đúng

    Hai quả bóng hình cầu có kích thước khác nhau, được đặt ở hai góc của một căn nhà hình hộp chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của căn nhà đó. Biết rằng trên bề mặt của mỗi quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền nhà nó tiếp xúc lần lượt bằng 1, 2, 3. Tính tổng các bình phương của hai bán kính của hai quả bóng đó.

    Hướng dẫn:

    Hình vẽ minh họa

    Xét quả bóng tiếp xúc với hai bức tường, nền của căn nhà và chọn hệ trục tọa độ Oxyz như hình vẽ (tương tự với góc tường còn lại).

    Gọi I(a; a; a) là tâm của mặt cầu có bán kính R = a.

    Phương trình mặt cầu là: (S):(x - a)^{2}+ (y - a)^{2} + (z - a)^{2} = a^{2}\ \ \ (1)

    Xét điểm M(x; y; z) nằm trên mặt cầu sao cho

    d(M,(Oxz)) = 2, d(M,(Oyz)) = 1, d(M,(Oxy)) = 3.

    Suy ra M(2; 1; 3).

    Vì M thuộc mặt cầu (S) nên từ (1) ta có:

    (2 - a)^{2} + (1 - a)^{2} + (3 - a)^{2}= a^{2}

    \Leftrightarrow a^{2} - 6a + 7 = 0\Leftrightarrow \left\lbrack \begin{matrix}a_{1} = 3 + \sqrt{2} = R_{1} \\a_{2} = 3 - \sqrt{2} = R_{2} \\\end{matrix} ight.

    \Rightarrow {R_{1}}^{2} + {R_{2}}^{2} =22

  • Câu 7: Vận dụng cao
    Xác định bán kính mặt cầu

    Trong không gian với hệ tọa độ Oxyz, cho hai điểm S(0;0;1) và A(1;1;1). Hai điểm M(m;0;0),N(0 ;n;0) thay đổi sao cho m + n = 1 và m > 0,n > 0. Biết rằng luôn tồn tại một mặt cầu cố định đi qua A và tiếp xúc với mặt phẳng (SMN). Bán kính của mặt cầu đó là:

    Hướng dẫn:

    Phương trình mặt phẳng (SMN) là \frac{x}{m} + \frac{y}{n} + \frac{z}{1} =1

    \Leftrightarrow nx + my + mnz - mn =0.

    Gọi I(a;b;c) và R là tâm và bán kính của mặt cầu cố định.

    Ta có

    R = d(I;(SMN))

    = \frac{|na + mb + mnc -mn|}{\sqrt{n^{2} + m^{2} + m^{2}n^{2}}}

    = \frac{|(1 - m)a + mb + m(1 - m)(c -1)|}{\sqrt{1 - 2mn + m^{2}n^{2}}}

    = \frac{|(1 - m)a + mb + m(1 - m)(c -1)|}{1 - mn}

    = \frac{\left| (1 - c)m^{2} + (b + c - a- 1)m + a ight|}{m^{2} - m + 1}

    Mà R không đổi nên \frac{1 - c}{1} = \frac{b + c - a - 1}{- 1} =\frac{a}{1} = t \Rightarrow \left\{ \begin{matrix}a = t \\b = t \\c = 1 - t \\\end{matrix} ight., hay I(t;t;1- t).
    Mặt khác ta có R = IA = \sqrt{3t^{3} - 4t +2} = |t| \Rightarrow t = 1.

    Vậy R = 1.

  • Câu 8: Vận dụng
    Chọn đáp án thích hợp

    Tìm tập hợp các tâm I của mặt cầu

    (S): x^{2} + y^{2} + z^{2} - 6\cos t - 4\sin ty + 6z\cos 2t - 3 = 0, t\mathbb{\in R}.

    Hướng dẫn:

    Ta có:

    a = 3cost;b = 2sint;c = - 3;d = cos2t - 3 = - 2sin^{2}t - 2

    \Rightarrow 9cos^{2}t + 4sin^{2}t + 2sin^{2}t + 11 > 0,\ \ \forall t\mathbb{\in R}

    Tâm I:x = 3cost;y = 2sint;z = - 3

    \Rightarrow \frac{x^{2}}{9} + \frac{y^{2}}{4} = 1;\ \ z + 3 = 0

    Vậy tập hợp các tâm I là elip \frac{x^{2}}{9} + \frac{y^{2}}{4} = 1;z + 3 = 0

  • Câu 9: Thông hiểu
    Xác định phương trình đường thẳng d

    Cho mặt cầu (S):x^{2} + y^{2} + z^{2} - 2x + 4y + 2z - 3 = 0 và mặt phẳng (P):x + y - 2z + 4 = 0. Phương trình đường thẳng d tiếp xúc với mặt cầu (S) tại A(3; - 1;1) và song song với mặt phẳng (P) là:

    Hướng dẫn:

    Mặt cầu (S) có tâm I(1; - 2; - 1) \Rightarrow \overrightarrow{IA} = (2;1;2)

    Đường thẳng d tiếp xúc với mặt cầu (S) tại \left\lbrack \begin{matrix} t = \frac{7}{2} \\ t = - 1 \\ \end{matrix} \right. và song song với mặt phẳng (P) nên đường thẳng d có vettơ chỉ phương \overrightarrow{a_{d}} = \left\lbrack \overrightarrow{n_{(P)}},\overrightarrow{IA} \right\rbrack = (4; - 6; - 1)

    Vậy phương trình đường thẳngd:\left\{ \begin{matrix} x = 3 + 4t \\ y = - 1 - 6t \\ z = 1 - t \\ \end{matrix} \right.\ .

  • Câu 10: Thông hiểu
    Tìm biểu thức liên hệ

    Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với  AB=2a, AD=a. Cạnh bên SA vuông góc với đáy và góc giữa SC với đáy bằng 45^0 . Gọi N là trung điểm SA, h là chiều cao của khối chóp S.ABCD và R là bán kính mặt cầu ngoại tiếp khối chóp N.ABC. Biểu thức liên hệ giữa R và h là:

    Hướng dẫn:

    Tìm biểu thức liên hệ

    Ta có {45^0} = \widehat {SC,\left( {ABCD} ight)} = \widehat {SC,AC} = \widehat {SCA} .

    Trong \Delta SAC, ta có h = SA = a\sqrt 5

    Ta có \left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} ight. \Rightarrow BC \bot \left( {SAB} ight) \Rightarrow BC \bot BN.

    Mặt khác, ta lại có NA \bot AC.

    Do đó hai điểm A, B cùng nhìn đoạn dưới một góc vuông nên hình chóp N.ABC nội tiếp mặt cầu tâm J là trung điểm NC, bán kính

    R = JN = \frac{{NC}}{2} = \frac{1}{2}.\sqrt {A{C^2} + {{\left( {\frac{{SA}}{2}} ight)}^2}} = \frac{{5a}}{4}.

  • Câu 11: Vận dụng
    Tính bán kính đường tròn

    Trong không gian với hệ tọa độ Oxyz, cho điểm M thuộc mặt cầu (S): (x − 3)^2 + (y + 1)^2 + z^ 2 = 9 và ba điểm A(1; 0; 0), B(2; 1; 3), C(0; 2; −3). Biết rằng quỹ tích các điểm M thỏa mãn MA^{2} + 2\overrightarrow{MB}.\overrightarrow{MC}= 8 là đường tròn cố định, tính bán kính r đường tròn này?

    Hướng dẫn:

    Ta có:\left\{ \begin{matrix}\overrightarrow{MA} = (1 - x; - y; - z) \\\overrightarrow{MB} = (2 - x;1 - y;3 - z) \\\overrightarrow{MC} = ( - x;2 - y; - 3 - z) \\\end{matrix} ight. khi đó:

    MA^{2} +2\overrightarrow{MB}.\overrightarrow{MC} = 8

    \Leftrightarrow (x - 1)^{2} + y^{2} +z^{2} + 2\left\lbrack x(x - 2) + (y - 1)(y - 2) + (z - 3)(z + 3)ightbrack = 8

    \Leftrightarrow 3.\left( x^{2} + y^{2} +z^{2} ight) - 6x - 6y - 21 = 0

    \Leftrightarrow M \in (S'):x^{2} +y^{2} + z^{2} - 2x - 2y - 7 = 0

    Mà M \in (S):(x - 3)^{2} + (y + 1)^{2} +z^{2} = 9

    \Leftrightarrow x^{2} + y^{2} + z^{2} -6x + 2y + 1 = 0

    Suy ra M ∈ (P): 4x − 4y − 8 = 0.

    Như vậy quỹ tích điểm M là đường tròn giao tuyến của (S) tâm I(3; −1; 0), bán kính R = 3 và (P)

    Ta có: d\left( I;(P) ight) = \sqrt{2}\Leftrightarrow r = \sqrt{R^{2} - d^{2}} = \sqrt{7}

  • Câu 12: Thông hiểu
    Tìm phương trình mặt cầu

    Cho mặt phẳng (P):2x + 3y + z - 2 = 0 . Mặt cầu (S) có tâm I thuộc trục Oz, bán kính bằng \frac{2}{\sqrt{14}} và tiếp xúc mặt phẳng (P) có phương trình:

    Hướng dẫn:

    Vì tâmI \in Oz \Rightarrow I(0;0;z)

    Mặt cầu (S)có tâm I tiếp xúc với mặt phẳng

    (P) \Leftrightarrow d\left( I,(\beta) \right) = R \Leftrightarrow \frac{|2.0 + 3.0 + 1.z - 2|}{\sqrt{2^{2} + 3^{2} + 1^{2}}} = \frac{2}{\sqrt{14}}

    \Leftrightarrow |z - 2| = 2 \Leftrightarrow \left\lbrack \begin{matrix} z = 0 \Rightarrow I(0;0;0) \\ z = 4 \Rightarrow I(0;0;4) \\ \end{matrix} \right.

    Vậy phương trình mặt cầu .(S):x^{2} + y^{2} + z^{2} = \frac{2}{7} hoặc (S):x^{2} + y^{2} + (z - 4)^{2} = \frac{2}{7}.

  • Câu 13: Vận dụng cao
    Tìm giá trị của m thỏa mãn điều kiện

    Trong không gian tọa độ Oxyzcho mặt cầu (S):x^{2} + y^{2} + z^{2} + 4x - 6y + m = 0 và đường thẳng \Delta là giao tuyến của hai mặt phẳng (\alpha):x + 2y - 2z - 4 = 0 và (\beta):2x - 2y - z + 1 = 0. Đường thẳng \Delta cắt mặt cầu (S) tại hai điểm phân biệt A,B thỏa mãn AB = 8 khi:

    Hướng dẫn:

    Ta có \left\{ \begin{matrix} x + 2y - 2z - 4 = 0 \\ 2x - 2y - z + 1 = 0 \end{matrix} \right..

    Phương trình tham số của \Delta là \left\{ \begin{matrix} x = - 2 + 2t \\ y = t \\ z = - 3 + 2t \end{matrix} \right..

    A \in (\Delta) \Rightarrow A( - 2 + 2t;t; - 3 + 2t).

    A \in (S) \Rightarrow ( - 2 + 2t)^{2} + t^{2} + ( - 3 + 2t)^{2} + 4( - 2 + 2t) - 6t + m = 0 (*).

    (*) \Leftrightarrow 9t^{2} - 18t + 5 + m = 0.

    Phương trình (*) có hai nghiệm phân biệt khi \Delta' = 36 - 9m > 0 \Leftrightarrow m < 4.

    Khi đó A\left( - 2 + 2t_{1};t_{1}; - 3 + 2t_{1} \right),B\left( - 2 + 2t_{2};t_{2}; - 3 + 2t_{2} \right).

    t_{1} + t_{1} = 2,t_{1}t_{2} = \frac{5 + m}{9}.

    AB = 8 \Leftrightarrow AB^{2} = 64.

    Suy ra 9\left( t_{2} - t_{1}\right)^{2} = 64 \Leftrightarrow 9\left\lbrack \left( t_{1} + t_{2}\right)^2- 4t_{1}t_{2} \right\rbrack = 64

    \Rightarrow 9.\left\lbrack 2^2 -4\left( \frac{5 + m}{9} \right) \right\rbrack = 64 \Leftrightarrow m = -12.

    Cách 2:

    Mặt cầu (S) có tâm I( - 2;3;0), R = \sqrt{13 - m}, m < 13.

    Đường thẳng (\Delta) qua M_{0}( - 2;0; - 3), có VTCP \overrightarrow{u} = (2;1;2)

    d = d\left( I;(\Delta) \right) = \frac{\left| \left\lbrack \overrightarrow{IM_{0}};\overrightarrow{u} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = 3

    Yêu cầu đề bài tương đương R^{2} = \frac{AB^{2}}{4} + d^{2} \Leftrightarrow 13 - m = 16 + 9 \Leftrightarrow m = - 12\ (n).

  • Câu 14: Vận dụng
    Tìm tọa độ điểm M

    Trong không gian Oxyz, cho điểm A(0; 1; 2), mặt phẳng (α): x−y +z −4 = 0 và mặt cầu (S):(x - 3)^{2} + (y - 1)^{2} + (z - 2)^{2} = 16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x’Ox là

    Hướng dẫn:

    Gọi (C) là giao tuyến của mặt phẳng (P) và mặt cầu (S) và (C) có tâm H, bán kính r.

    Bán kính r của đường tròn là nhỏ nhất khi và chỉ khi IH lớn nhất khi và chỉ khi d(I,(P)) lớn nhất.

    Vì M ∈ x'Ox nên gọi M(m; 0; 0).

    Suy ra mặt phẳng (P) chứa AM và (P) ⊥ (α).

    Khi đó \overrightarrow{n_{(P)}} = \left\lbrack \overrightarrow{MA};\overrightarrow{n_{(\alpha)}} ightbrack = (3;2 + m;m - 1)

    Mà mặt phẳng (P) đi qua A nên phương trình của mặt phẳng (P) là:

    3(x − 0) + (2 + m)(y − 2) + (m − 1)(z − 2) = 0 hay 3x + (2 + m)y + (m − 1)z −3m=0

    Ta có:

    d\left( I;(P) ight) = \frac{9}{\sqrt{2m^{2} + 2m + 14}} lớn nhất khi và chỉ khi 2m^{2} + 2m + 14 đạt giá trị nhỏ nhất

    Mà 2m^{2} + 2m + 14 = 2\left( m + \frac{1}{2} ight)^{2} + \frac{27}{2} \geq \frac{27}{2}

    Do đó 2m^{2} + 2m + 14 nhỏ nhất khi và chỉ khi m = - \frac{1}{2}

    Vậy M\left( - \frac{1}{2};0;0 ight).

  • Câu 15: Vận dụng
    Xác định phương trình mặt cầu

    Cho đường thẳng d: \frac{x - 1}{2} = \frac{y - 2}{1} = \frac{z - 3}{2} và hai mặt phẳng \left( P_{1} \right):\ \ x\ + \ 2y\ + \ 2z\ - \ 2\ = \ 0;\ \ \left( P_{2} \right):\ \ 2x\ + \ y\ + \ 2z\ - \ 1\ = \ 0. Mặt cầu có tâm I nằm trên d và tiếp xúc với 2 mặt phẳng \left( P_{1} \right),\ \left( P_{2} \right), có phương trình:

    Hướng dẫn:

    Ta có:

    I \in d\ \ \Rightarrow I(2t + 1;\ t + 2;\ 2t + 3)

    Mặt cầu tiếp xúc với 2 mặt phẳng \Leftrightarrow d\left( I;\left( P_{1} \right) \right) = d\left( I;\ \left( P_{2} \right) \right)

    \Leftrightarrow |8t + 9| = |9t + 9|

    \Leftrightarrow \left\lbrack \begin{matrix} 8t + 9 = 9t + 9 \\ 8t - 9 = - 9t - 9 \\ \end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix} t = 0 \\ t = \frac{- 18}{17} \\ \end{matrix} \right.

    Với t = 0 \Rightarrow \ I(1;2;3);\ \ R = 3 \Rightarrow (S):(x - 1)^{2} + (y - 2)^{2} + (z - 3)^{2} = 9.

    Với t = - \frac{18}{17} \Rightarrow I\left( - \frac{19}{17};\frac{16}{17};\frac{15}{17} \right);R = \frac{3}{17} \Rightarrow (S):\left( x + \frac{19}{17} \right)^{2} + \left( y - \frac{16}{17} \right)^{2} + \left( z - \frac{15}{17} \right)^{2} = \frac{9}{289}.

  • Câu 16: Vận dụng
    Tìm bán kính mặt cầu

    Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và BA = BC = a. Cạnh bên SA = 2a và vuông góc với mặt phẳng đáy. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC  là:

    Hướng dẫn:

     Tìm bán kính

    Gọi M là trung điểm AC, suy ra M là tâm đường tròn ngoại tiếp tam giác ABC.

    Gọi I là trung điểm SC, suy ra IM ||SA nên IM \bot \left( {ABC} ight) .

    Do đó IM là trục của \triangle ABC, suy ra IA=IB=IC     (1)

    Hơn nữa, tam giác SAC vuông tại A có I là trung điểm SC nên IS=IC=IA.  (2)

    Từ (1) và (2) , ta có IS=IA=IB=IC

    hay I là tâm của mặt cầu ngoại tiếp hình chóp S.ABC.

    Vậy bán kính R = IS = \frac{{SC}}{2} = \frac{{\sqrt {S{A^2} + A{C^2}} }}{2} = \frac{{a\sqrt 6 }}{2} .

  • Câu 17: Vận dụng
    Chọn đáp án đúng

    Cho hai điểm A(2, - 3, - 1);\ \ \ B( - 4,5, - 3). Tìm tập hợp các điểm M(x,y,z) thỏa mãn \frac{MA}{MB} = \frac{\sqrt{3}}{2}

    Hướng dẫn:

    Theo bài ra ta có:

    2MA = \sqrt{3}MB \Leftrightarrow 4MA^{2} = 3MB^{2}

    \Leftrightarrow 4\left\lbrack (2 - x)^{2} + ( - 3 - y)^{2} + ( - 1 - z)^{2} \right\rbrack

    = 3\left\lbrack ( - 4 - x)^{2} + (5 - y)^{2} + ( - 3 - z)^{2} \right\rbrack

    Mặt cầu x^{2} + y^{2} + z^{2} - 40x - 54y - 10z - 94 = 0

  • Câu 18: Vận dụng
    Xác định tọa độ tâm I

    Cho tứ diện ABCD có A(3,6, - 2);B(6,0,1);C( - 1,2,0);D(0,4,1). Tâm I của mặt cầu ngoại tiếp tứ diện ABCD có tọa độ:

    Hướng dẫn:

    Gọi I(x,y,z) là tâm cầu ngoại tiếp tứ diện ABCD. Tọa độ của I là nghiệm của hệ phương trình:

    \left\{ \begin{matrix} AI^{2} = BI^{2} \\ BI^{2} = CI^{2} \\ CI^{2} = DI^{2} \\ \end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix} (x - 3)^{2} + (y - 6)^{2} + (z + 2)^{2} = (x - 6)^{2} + y^{2} + (z - 1)^{2} \\ (x - 6)^{2} + y^{2} + (z - 1)^{2} = (x + 1)^{2} + (y - 2)^{2} + z^{2} \\ (x + 1)^{2} + (y - 2)^{2} + z^{2} = x^{2} + (y - 4)^{2} + (z - 1)^{2} \\ \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} 6x - 12y + 6z = - 12 \\ - 14x + 4y - 2z = - 32 \\ 2x + 4y + 2z = 12 \\ \end{matrix} \right.

    \Leftrightarrow \left\{ \begin{matrix} x - 2y + z = - 2 \\ 7x - 2y + z = 16 \\ x + 2y + z = 6 \\ \end{matrix} \right. \Leftrightarrow \left\{ \begin{matrix} x = 3 \\ y = 2 \\ z = - 1 \\ \end{matrix} \right.\ \Rightarrow I(3,2, - 1)

  • Câu 19: Vận dụng
    Viết phương trình mặt phẳng

    Trong không gian với hệ tọa độ Oxyz, cho (S):(x - 1)^{2} + (y - 1)^{2} + (z - 1)^{2} = 1 và điểm A(2;2;2). Xét các điểm M \in (S) sao cho đường thẳng AM luôn tiếp xúc với (S). Điểm M luôn thuộc một mặt phẳng cố định có phương trình là

    Hướng dẫn:

    Tọa độ tâm mặt cầu là:I(1;1;1)

    Gọi M(x;y;z) khi đó: \left\{ \begin{matrix} \overrightarrow{AM} = (x - 2;y - 2;z - 2) \\ \overrightarrow{IM} = (x - 1;y - 1;z - 1) \\ \end{matrix} ight..

    Theo đề bài ra ta có:

    \overrightarrow{AM}.\overrightarrow{IM} = 0

    \Leftrightarrow (x - 2)(x - 1) + (y - 2)(y - 1) + (z - 2)(z - 1) = 0

    \Leftrightarrow x^{2} + y^{2} + z^{2} - 3x - 3y - 3z + 6 = 0(*)

    Mặt khác phương trình mặt cầu

    (S):(x - 1)^{2} + (y - 1)^{2} + (z - 1)^{2} = 1

    \Rightarrow x^{2} + y^{2} + z^{2} - 2x - 2y - 2z + 2 = 0(**)

    Lấy (*) trừ (**) ta được: x + y + z - 4 = 0.

  • Câu 20: Vận dụng
    Chọn đáp án chính xác

    Cho hai đường thẳng d:\left\{ \begin{matrix} x = 2t \\ y = t \\ z = 4 \\ \end{matrix} \right.và d':\left\{ \begin{matrix} x = t^{'} \\ y = 3 - t' \\ z = 0 \\ \end{matrix} \right.. Phương trình mặt cầu có đường kính là đoạn thẳng vuông góc chung của đường thẳng d và d’ là:

    Hướng dẫn:

    Gọi A(2t;t;4) \in d;B(t';3 -t';0) \in d'

    \Rightarrow \overrightarrow{AB} = (t' - 2t;3 - t' - t; - 4),\overrightarrow{u_{d}} = (2;1;0),\ \overrightarrow{u_{d'}} = (1; - 1;0)

    Ta có: \left\{ \begin{matrix} \overrightarrow{AB}.\overrightarrow{u_{d}} = 0 \\ \overrightarrow{AB}.\overrightarrow{u_{d'}} = 0 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} t = 1 \Rightarrow A(2;1;4) \\ t' = 2 \Rightarrow B(2;1;0) \\ \end{matrix} \right.

    \Rightarrow I(2;1;2) và R = 2 \Rightarrow (x - 2)^{2} + (y - 1)^{2} + (z - 2)^{2} = 4.

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (30%):
    2/3
  • Thông hiểu (45%):
    2/3
  • Vận dụng (25%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
1
18 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Lớp 12
Xem thêm