Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Trắc nghiệm Toán 12 Kết nối tri thức
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Dễ)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Nhận biết
    Tìm khẳng định sai

    Giả sử A và B là hai biến cố ngẫu nhiên thỏa mãn P(A) > 0 và 0 < P(B) < 1. Khẳng định nào dưới đây sai?

    Hướng dẫn:

    Giả sử A và B là hai biến cố ngẫu nhiên thỏa mãn P(A) > 0 và 0 < P(B) < 1.

    Khi đó, công thức Bayes:

    P\left( B|A \right) = \frac{P(B)P\left( A|B \right)}{P(B)P\left( A|B \right) + P\left( \overline{B} \right)P\left( A|\overline{B} \right)}

    Hay còn có thể viết dưới dạng: P\left( B|A \right) = \frac{P(B)P\left( A|B \right)}{P(A)}.

  • Câu 2: Nhận biết
    Tính xác suất P

    Cho hai biến cố A và B với P(B) = 0,2;P\left( A|B ight) = 0,5;P\left( A|\overline{B} ight) = 0,4. Tính P\left( B|A ight)?

    Hướng dẫn:

    Ta có: P(B) = 0,2 \Rightarrow P\left( \overline{B} ight) = 1 - P(B) = 1 - 0,2 = 0,8

    Áp dụng công thức Bayes:

    P\left( B|A ight) = \frac{P(B).P\left( A|B ight)}{P(B).P\left( A|B ight) + P\left( \overline{B} ight).P\left( A|\overline{B} ight)}

    \Rightarrow P\left( B|A ight) = \frac{0,2.0,5}{0,2.0,5 + 0,8.0,4} = \frac{5}{21} \approx 0,238 .

  • Câu 3: Thông hiểu
    Tính xác suất người được chọn là đàn ông

    Được biết có 5\% đàn ông bị mù màu và 0,25\% phụ nữ bị mù màu (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics – Understanding why and how, Springer, 2005). Giả sử số đàn ông bằng số phụ nữ. Chon một người bị mù màu. Xác suất để người đó là đàn ông là bao nhiêu?

    Hướng dẫn:

    Gọi A là biến cố người được chọn là đàn ông, B là biến cố người được chọn mù màu.

    Theo đề bài ra ta có P\left( \left. \ B \right|A \right) = 0,05;P\left( \left. \ B \right|\overline{A} \right) = 0,0025.

    Vì số đàn ông bằng số phụ nữ nên ta có P(A) = P\left( \overline{A} \right) = 0,5.

    Áp dụng công thức Bayes ta có xác suất để chọn được một người đàn ông mù màu là:

    P\left( \left. \ A \right|B \right) =\frac{P(A).P\left( \left. \ B \right|A \right)}{P(A).P\left( \left. \ B \right|A \right) + P\left( \overline{A} \right).P\left( \left. \ B\right|\overline{A} \right)}

    = \frac{0,5.0,05}{0,5.0,05 + 0,5.0,0025} = \frac{20}{21}.

  • Câu 4: Nhận biết
    Tính P(A|B)

    Cho hai biến cố A và B với P(A) = 0,2; P(B) = 0,26; P\left( B|A \right) = 0,7. Tính P\left( A|B \right).

    Hướng dẫn:

    Ta có: P\left( A|B \right) = \frac{P(A).P\left( B|A \right)}{P(B)} = \frac{0,2.0,7}{0,26} = \frac{7}{13}.

  • Câu 5: Nhận biết
    Tính xác suất của biến cố

    Cho hai biến cố A,B sao cho P(A) = 0,3; P(B) = 0,6 và P(A|B) = 0,2. Tính P(B|A).

    Hướng dẫn:

    Ta có P(B|A) = \frac{P(B).P(A|B)}{P(A)} = \frac{0,6.0,2}{0,3} = \frac{2}{5}.

  • Câu 6: Nhận biết
    Tính P(B|A)

    Cho hai biến cố A,B thỏa mãn P(A) = 0,4, P(B) = 0,3, P(A|B) = 0,25. Khi đó, P(B|A) bằng

    Hướng dẫn:

    Theo công thức Bayes, ta có:

    P(B|A) = \frac{P(B).P(A|B)}{P(A)} = \frac{0,3.0,25}{0,4} = 0,1875.

  • Câu 7: Nhận biết
    Tính P(B|A)

    Cho hai biến cố A và B, với P(B) = 0,8, P\left( A|B \right) = 0,7, P\left( A|\overline{B} \right) = 0,45. Tính P\left( B|A \right).

    Hướng dẫn:

    Ta có: P\left( \overline{B} \right) = 1 - 0,8 = 0,2.

    Công thức Bayes:

    P\left( B|A \right) = \frac{P(B)P\left( A|B \right)}{P(B)P\left( A|B \right) + P\left( \overline{B} \right)P\left( A|\overline{B} \right)}

    \Rightarrow P\left( B|A \right) = \frac{0,8.0,7}{0,8.0,7 + 0,2.0,45} = \frac{56}{65}.

  • Câu 8: Nhận biết
    Chọn đáp án đúng

    Cho hai biến cố A và B sao cho P(A) = 0,6; P(B) = 0,4; P\left( A|B \right) = 0,3. Khi đó P\left( B|A \right) bằng?

    Hướng dẫn:

    Áp dụng công thức Bayes, ta có:

    P\left( B|A \right) = \frac{P(B)P\left( A|B \right)}{P(A)} = \frac{0,4.0,3}{0,6} = 0,2.

  • Câu 9: Thông hiểu
    Xét tính đúng sai của các phương án

    Giả sử 5\% email của bạn nhận được là email rác. Bạn sử dụng một hệ thống lọc email rác mà khả năng lọc đúng email rác của hệ thống này là 95\% và có 10\% những email không phải là email rác nhưng vẫn bị lọc. Các khẳng định sau đúng hay sai?

    Hướng dẫn:

    a) Gọi A: “Email nhận được là email rác”.

    Và B: “Email bị lọc đúng email rác của hệ thống lọc email rác”.

    Vì 5% email nhận được là rác nên xác suất nhận được một email rác là

    P(A) = 5\% = 0,05

    b) Xác suất email bị lọc của email rác là P\left( B|A ight) = 95\% = 0,95.

    c) Xác suất email nhận được không phải rác là P\left( \overline{A} ight) = 1 - P(A) = 1 - 0,05 = 0,95

    Xác suất email bị lọc của email không phải rác là P\left( B|\overline{A} ight) = 0,1

    Vậy xác suất chọn một email bị lọc bất kể là rác hay không là

    P(B) = P(A).P\left( B|A ight) + P\left( \overline{A} ight)P\left( B|\overline{A} ight)

    \Rightarrow P(B) = 0,95.0,05 + 0,1.0,95 = 0,1425

    d) Xác suất chọn một email trong số những email bị lọc thực sự là email rác là

    P\left( A|B ight) = \frac{P\left( B|A ight).P(A)}{P(B)} = \frac{0,95.0,05}{0,1425} = \frac{1}{3}.

  • Câu 10: Nhận biết
    Chọn đáp án đúng

    Cho hai biến cố A và B, công thức tính xác suất toàn phần là

    Hướng dẫn:

    Ta có: P(A) = P(B).P\left( A|B \right) + P\left( \overline{B} \right).P\left( A|\overline{B} \right)

  • Câu 11: Nhận biết
    Tính giá trị của P(A)

    Cho hai biến cố A và B, với P(B) = 0,8, P\left( A|B \right) = 0,7, P\left( A|\overline{B} \right) = 0,45. Giá trị P(A) bằng

    Hướng dẫn:

    Ta có: P\left( \overline{B} \right) = 1 - P(B) = 1 - 0,8 = 0,2

    Công thức xác suất toàn phần

    P(A) = P(B).P\left( A|B \right) + P\left( \overline{B} \right).P\left( A|\overline{B} \right)= 0,8.0,7 + 0,2.0,45 = 0,65

  • Câu 12: Nhận biết
    Tính P(A)

    Cho hai biến cố A,B với P(B) = 0,6, P(A|B) = 0,7 và P(A|\overline{B}) = 0,4. Khi đó P(A) bằng

    Hướng dẫn:

    Ta có: P(\overline{B}) = 1 - P(B) = 1 - 0,6 = 0,4.

    Theo công thức xác suất toàn phần:

    P(A) = P(B).P\left( A \middle| B \right) + P\left( \overline{B} \right).P\left( A \middle| \overline{B} \right)

    = 0,6.0,7 + 0,4.0,4 = 0,58.

  • Câu 13: Nhận biết
    Tính P(A|B)

    Cho hai biến cố A và B là hai biến cố độc lập, với P(A) = 0,2, P(B) = 0,4. Tính P\left( A|B \right).

    Hướng dẫn:

    Ta có:

    A và B là hai biến cố độc lập nên: P\left( A|B \right) = P(A) = 0,2.

  • Câu 14: Thông hiểu
    Chọn đáp án đúng

    Một phân xưởng có 3 máy tự động: máy I sản xuất 25%, máy II sản xuất 30%, máy III sản xuất 45% số sản phẩm. Tỷ lệ phế phẩm tương ứng của các máy lần lượt là 0,1%, 0,2% và 0,3%. Chọn ngẫu nhiên ra một sản phẩm của phân xưởng. 1. Tìm xác suất nó là phế phẩm.

    Hướng dẫn:

    Gọi Ai là "lấy ra sản phẩm từ lô i" thì A1, A2, A3 tạo thành hệ đầy đủ.

    Gọi A là "lấy ra sản phẩm là phế phẩm".

    Áp dụng công thức xác suất toàn phần, ta có

    P(A) = P\left( A_{1} ight)P\left( A|A_{1} ight) + P\left( A_{2} ight)P\left( A|A_{2} ight) + P\left( A_{3} ight)P\left( A|A_{3} ight)

    \Rightarrow P(A) = 0,25.0,1\% + 0,3.0,2\% + 0,45.0,3\% = 0,22\%

  • Câu 15: Nhận biết
    Chọn đáp án đúng

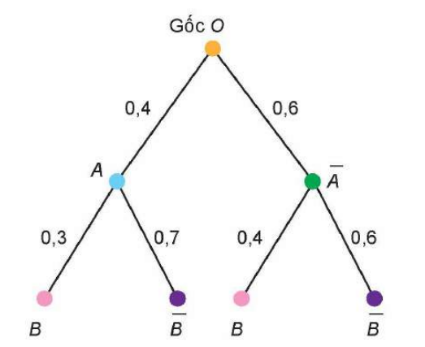
    Cho A và B là các biến cố của phép thử T. Biết rằng P(A) > 0;0 < P(B) < 1. Xác suất của biến cố B với điều kiện biến cố A đã xảy ra được tính theo công thức nào sau đây?

    Hướng dẫn:

    Theo công thức Bayes ta có:

    P\left( B|A ight) = \frac{P(B).P\left( A|B ight)}{P(B).P\left( A|B ight) + P\left( \overline{B} ight).P\left( A|\overline{B} ight)}

  • Câu 16: Nhận biết
    Chọn đáp án đúng

    Cho hai biến cố A;B với P(B) = 0,6;P\left( A|B ight) = 0,7;P\left( A|\overline{B} ight) = 0,4. Giá trị P(A) bằng:

    Hướng dẫn:

    Ta có: P\left( \overline{B} ight) = 1 - P(B) = 1 - 0,6 = 0,4

    Theo công thức xác suất toàn phần, ta có:

    P(A) = P(B).P\left( A|B ight) + P\left( \overline{B} ight).P\left( A|\overline{B} ight)

    \Rightarrow P(A) = 0,6.0,7 + 0,4.0,4 = 0,58

  • Câu 17: Nhận biết
    Tính P(A)

    Cho hai biến cố A,\ B thỏa mãn P\left( \overline{B} \right) = 0,2;\ P\left( A|B \right) = 0,5;\ P\left( \left. \ A \right|\overline{B} \right) = 0,3. Khi đó, P(A) bằng

    Hướng dẫn:

    Ta có: P(B) = 1 - P\left( \overline{B} \right) = 0,8.

    Theo công thức xác suất toàn phần, ta có:

    P(A) = P(B).P\left( A|B \right) + P\left( \overline{B} \right).P\left( A|\overline{B} \right)

    = 0,8.0,5 + 0,2.0,3 = 0,46.

  • Câu 18: Thông hiểu
    Chọn đáp án chính xác

    Lớp 10A có 35 học sinh, mỗi học sinh đều giỏi ít nhất một trong hai môn Toán hoặc Văn. Biết rằng có 23 học sinh giỏi môn Toán và 20 học sinh giỏi môn Văn. Chọn ngẫu nhiên một học sinh của lớp 10A. Tính xác suất để học sinh được chọn "không giỏi môn Văn biết rằng học sinh đó giỏi môn Toán". (Làm tròn đến hàng phần trăm).

    Hướng dẫn:

    Trong số 23 học sinh giỏi Toán, có đúng 8 học sinh giỏi cả Toán và Văn nên số học sinh không giỏi Văn mà giỏi Toán là 23 - 8 = 15.

    Xác suất để học sinh được chọn "không giỏi môn Văn biết rằng học sinh đó giỏi môn Toán" là P = \frac{15}{23} \approx 0,65

  • Câu 19: Thông hiểu
    Chọn đáp án đúng

    Có hai hộp bên ngoài giống nhau:

    Hộp thứ nhất đựng 1 sản phẩm lỗi và 9 sản phẩm tốt.

    Hộp thứ hai đựng 2 sản phẩm lỗi và 8 sản phẩm tốt.

    Lấy ngẫu nhiên một hộp, sau đó lấy ngẫu nhiên một sản phẩm. Xác suất để được sản phẩm tốt là:

    Hướng dẫn:

    Gọi A1 là biến cố lấy sản phẩm từ hộp thứ nhất.

    A2 là biến cố lấy sản phẩm từ hộp thứ hai.

    Vì chọn ngẫu nhiên nên P\left( A_{1} ight) = P\left( A_{2} ight) = \frac{1}{2}

    Gọi B là biến cố lấy được sản phẩm tốt ta có:

    P\left( B|A_{1} ight) = \frac{9}{10};P\left( B|A_{2} ight) = \frac{8}{10}

    Do đó:

    P(B) = P\left( A_{1} ight).P\left( B|A_{1} ight) + P\left( A_{2} ight).P\left( B|A_{2} ight)

    \Rightarrow P(B) = \frac{1}{2}.\frac{9}{10} + \frac{1}{2}.\frac{8}{10} = \frac{17}{20} = 0,85

  • Câu 20: Nhận biết
    Chọn đáp án đúng

    Cho hai biến cố A và B với 0 < P(B) < 1. Khi đó

    Hướng dẫn:

    Ta có: P(A) = P(B)P\left( \left. \ A \right|B \right) + P\left( \overline{B} \right)P\left( \left. \ A \right|\overline{B} \right)

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (75%):
    2/3
  • Thông hiểu (25%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
1
4 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Trắc nghiệm Toán 12 Kết nối tri thức
Xem thêm