VnDoc.com Lớp 12 Trắc nghiệm Toán 12 Kết nối tri thức

Đóng

Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm

Mua VnDoc PRO chỉ từ 79.000đ

Đóng

Bạn cần đăng nhập tài khoản Thành viên VnDoc để:

- Xem đáp án

- Nhận 1 lần làm bài trắc nghiệm miễn phí!

Đăng nhập

Bài tập trắc nghiệm Toán 12 KNTT Bài 10 (Mức độ Vừa)

Nhận biết Thông hiểu Vận dụng Vận dụng cao

Bài kiểm tra này bao gồm 15 câu
Điểm số bài kiểm tra: 15 điểm
Xem lại kỹ lý thuyết trước khi làm bài
Chuẩn bị giấy và bút để nháp trước khi bắt đầu

Bắt đầu!!

00:00:00

Câu 1: Thông hiểu

Tính độ lệch chuẩn của mẫu số liệu

Năng suất lúa (đơn vị: tấn/ha) của một số thửa ruộng được ghi lại trong bảng sau:

Năng suất	[5,5; 5,7)	[5,7; 5,9)	[5,9; 6,1)	[6,1; 6,3)	[6,3; 6,5)	[6,5; 6,7)
Số thửa ruộng	3	4	6	5	5	2

Xác định độ lệch chuẩn của mẫu số liệu ghép nhóm?

A.
$0,09$
B.
$0,45$
C.
$0,02$
D.
$0,3$

Hướng dẫn:

Ta có:

Năng suất	[5,5; 5,7)	[5,7; 5,9)	[5,9; 6,1)	[6,1; 6,3)	[6,3; 6,5)	[6,5; 6,7)
Số thửa ruộng	3	4	6	5	5	2
Tần số tích lũy	3	7	13	18	23	25

Số trung bình của mẫu số liệu ghép nhóm:

$\overline{x} = \frac{3.5,6 + 4.5,8 + 6.6,0 + 5.6,2 + 5.6,4 + 2,6,6}{25} = 6,088$

Phương sai của mẫu số liệu ghép nhóm là:

$S^{2} = \frac{1}{25}\left( 3.5,6^{2} + 4.5,8^{2} + 6.6,0^{2} + 5.6,2^{2} + 5.6,4^{2} + 2,6,6^{2} ight) - 6,088^{2} \approx 0,086656$

Vậy độ lệch chuẩn của mẫu số liệu ghép nhóm là $S = \sqrt{S^{2}} \approx 0,3$

Câu 2: Thông hiểu
Tìm số trung bình của mẫu số liệu ghép nhóm
Thống kê tổng số giờ nắng trong tháng 9 tại khu vực A trong các năm từ 2004 đến 2023 được thống kê như sau:

111,6

134,9

130,3

134,2

140,9

109,3

154,4

156,3

116,1

96,7

105,2

80,8

80,8

110

109

139

145

161

126

114

Lập bảng tần số ghép nhóm với nhóm đầu tiên là [80; 98) và độ dài nhóm bằng 18. Tìm số trung bình của mẫu số liệu ghép nhóm?
- A.
  $\overline{x} = 125$
- B.
  $\overline{x} = 122$
- C.
  $\overline{x} = 120$
- D.
  $\overline{x} = 124$
Hướng dẫn:
Ta có bảng như sau:

Số giờ

[80; 98)

[98; 116)

[116; 134)

[134; 152)

[152; 170)

Giá trị đại diện

89

107

125

143

161

Số năm

3

6

3

5

3

Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x} = \frac{3.89 + 6.107 + 3.125 + 5.143 + 3.161}{20} = 124,1$
Câu 3: Thông hiểu
Tìm độ lệch chuẩn của mẫu số liệu ghép nhóm
Thống kê doanh thu (đơn vị: triệu đô la) của 20 công ty sản xuất ô tô trong năm 2023, người ta có bảng sau:

Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
- A.
  28,23
- B.
  24,88
- C.
  26,02
- D.
  20,76
Hướng dẫn:
Chọn giá trị đại diện cho mẫu số liệu, ta có:

Điểm trung bình là:

$\overline{x} = \frac{5 \cdot 10 + 5 \cdot 30 + 6 \cdot 50 + 2 \cdot 70 + 2 \cdot 90}{20} = 41$ .

Phương sai là:

$S^{2} = \frac{1}{20}\left\lbrack 5 \cdot (10)^{2} + 5 \cdot (30)^{2} + 6 \cdot (50)^{2} + 2 \cdot (70)^{2} + 2 \cdot (90)^{2} \right\rbrack - (41)^{2} = 619$ .

Độ lệch chuẩn: $S = \sqrt{619} \approx 24,88$ .
Câu 4: Thông hiểu
Tìm độ lệch chuẩn của mẫu số liệu ghép nhóm
Điều tra về số tiền mua sách (đơn vị: nghìn đồng) trong một năm của 50 học sinh trong một trường THPT, người ta có bảng sau:

Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
- A.
  233,98
- B.
  265,34
- C.
  242,29
- D.
  264,12
Hướng dẫn:
Chọn giá trị đại diện cho mẫu số liệu, ta có:

Điểm trung bình là:

$\overline{x} = \frac{29 \cdot 100 + 11 \cdot 300 + 3 \cdot 500 + 4 \cdot 700 + 3 \cdot 900}{50} = 264$ .

Phương sai là:

$S^{2} = \frac{1}{50}\lbrack 29 \cdot (100)^{2} + 11 \cdot (300)^{2} + 3 \cdot (500)^{2}$ $+ 4 \cdot (700)^{2} + 3 \cdot (900)^{2}\rbrack - (264)^{2} = 58704$ .

Độ lệch chuẩn: $S = \sqrt{58704} \approx 242,29$ .
Câu 5: Nhận biết
Tính số trung bình của mẫu số liệu ghép nhóm
Cho mẫu dữ liệu ghép nhóm như sau:

Đối tượng

[120; 122)

[122; 124)

[124; 126)

[126; 128)

[128; 130)

Tần số

8

9

12

10

11

Tính số trung bình của mẫu số liệu?
- A.
  $124,13$
- B.
  $126,85$
- C.
  $126,08$
- D.
  $125,28$
Hướng dẫn:
Cỡ mẫu $N = 50$

Đối tượng

[120; 122)

[122; 124)

[124; 126)

[126; 128)

[128; 130)

Giá trị đại diện

121

123

125

127

129

Tần số

8

9

12

10

11

Số trung bình của mẫu số liệu là:

$\overline{x} = \frac{8.121 + 9.123 + 12.125 + 10.127 + 11.129}{50} = 125,28$
Câu 6: Vận dụng
Chọn khẳng định đúng
Giá đóng cửa của một cổ phiếu là giá của cổ phiếu đó cuối một phiên giao dịch. Bảng sau thống kê giá đóng cửa (đơn vị: nghìn đồng) của hai mã cổ phiếu $A$ và $B$ trong $50$ ngày giao dịch liên tiếp.

Giá đóng cửa
$\lbrack 120;122)$ $\lbrack 122;124)$ $\lbrack 124;126)$ $\lbrack 126;128)$ $\lbrack 128;130)$

Số ngày giao dịch

của cổ phiếu $A$
$8$ $9$ $12$ $10$ $11$

Số ngày giao dịch

của cổ phiếu $B$
$16$ $4$ $3$ $6$ $21$

Người ta có thể dùng phương sai và độ lệch chuẩn để so sánh mức độ rủi ro của các loại cổ phiếu có giá trị trung bình gần bằng nhau. Cổ phiếu nào có phương sai, độ lệch chuẩn cao hơn thì được coi là có độ rủi ro lớn hơn. Chọn khẳng định đúng.
- A.
  Phương sai của mẫu số liệu của cổ phiếu $A$ lớn hơn phương sai của mẫu số liệu của cổ phiếu $B$ .
- B.
  Giá đóng cửa của cổ phiếu $A$ ít phân tán hơn giá đóng cửa của cổ phiếu $B$ .
- C.
  Giá đóng cửa của hai cổ phiếu $A$ và $B$ có độ phân tán như nhau.
- D.
  Giá đóng cửa của cổ phiếu $B$ ít phân tán hơn giá đóng cửa của cổ phiếu $A$ .
Hướng dẫn:
Ta có bảng thống kê theo giá trị đại diện

Giá đóng cửa
121 123 125 127 129

Số ngày giao dịch

của cổ phiếu $A$
$8$ $9$ $12$ $10$ $11$

Số ngày giao dịch

của cổ phiếu $B$
$16$ $4$ $3$ $6$ $21$

Xét mẫu số liệu của cổ phiếu $A$

Số trung bình của mẫu số liệu là

${\overline{x}}_{A} = \frac{1}{50}.(8.121 + 9.123 + 12.125 + 10.127 + 11.129) = 125,28$

Phương sai của mẫu số liệu ghép nhóm là

${S_{A}}^{2} = \frac{1}{50}.\left( 8.121^{2} + 9.123^{2} + 12.125^{2} + 10.127^{2} + 11.129^{2} \right) - 125,28^{2} = 7,5216$

Độ lệch chuẩn của mẫu số liệu ghép nhóm là

$S_{A} = \sqrt{7,5216}$

Xét mẫu số liệu của cổ phiếu $B$

Số trung bình của mẫu số liệu là

${\overline{x}}_{B} =\frac{1}{50}.(16.121 + 4.123 + 3.125 + 6.127 + 21.129)= 125,48$

Phương sai của mẫu số liệu ghép nhóm là

${S_{B}}^{2} = \frac{1}{50}.\left( 16.121^{2} + 4.123^{2} + 3.125^{2} + 6.127^{2} + 21.129^{2} \right) - 125,48^{2} = 12,4096$

Độ lệch chuẩn của mẫu số liệu ghép nhóm là

$S_{B} = \sqrt{12,4096}$

Ta có $S_{A} < S_{B}$ nên giá đóng cửa của cổ phiếu $A$ ít phân tán hơn giá đóng cửa của cổ phiếu $B$ .
Câu 7: Nhận biết
Chọn đáp án đúng
Cho mẫu số liệu ghép nhóm với bộ ba tứ phân vị lần lượt là $Q_{1} = 11,5$ ; $Q_{2} = 14,5$ ; $Q_{3} = 21,3.$ Khi đó khoảng tứ phân vị của mẫu số liệu trên là
- A.
  $\Delta Q = 3,0$ .
- B.
  $\Delta Q = 9,8$ .
- C.
  $\Delta Q = 32,8$ .
- D.
  $\Delta Q = 6,8$ .
Hướng dẫn:
Khoảng tứ phân vị của mẫu số liệu là: $\Delta Q = Q_{3} - Q_{1} = 21,3 - 11,5 = 9,8$ .
Câu 8: Thông hiểu
Tìm phương sai của mẫu số liệu ghép nhóm
Bảng dưới đây thống kê cự li ném tạ của một vận động viên.

Cự li (m)

[19; 19,5)

[19,5; 20)

[20; 20,5)

[20,5; 21)

[21; 21,5)

Tần số

13

45

24

12

6

Phương sai của mẫu số liệu ghép nhóm trên gần với giá trị nào sau đây nhất?
- A.
  $0.22.$
- B.
  $0.24$
- C.
  $0.28$
- D.
  $0.26$
Hướng dẫn:
Ta có:

Cự li (m)

[19; 19,5)

[19,5; 20)

[20; 20,5)

[20,5; 21)

[21; 21,5)

Giá trị đại diện

19,25

19,75

20,25

20,75

21,25

Tần số

13

45

24

12

6

Cỡ mẫu là n = 13 + 45 + 24 + 12 + 6 = 100.

Số trung bình của mẫu số liệu ghép nhóm là:

$\overline{x} = \frac{1}{100}\lbrack 13.19,25 + 45.19,75$

$+ 24.20,25 + 12.20,75 + 6.21,25) = 20,015$

Phương sai của mẫu số liệu ghép nhóm là:

$S^{2} = \frac{1}{100}\lbrack 13.(19,25)^{2} + 45.(19,25)^{2}$

$+ 24.(19,25)^{2} + 12.(19,25)^{2} + 6.(19,25)^{2}brack - (20,015)^{2} \approx 0,277$

Câu 9: Nhận biết

Hoàn thành bảng số liệu

Cho biểu đồ mức lương của công nhân hai phân xưởng A và B (đơn vị: triệu đồng) như sau:

Hoàn thành bảng số liệu sau:

Mức lương	[5; 6)	[6; 7)	[7; 8)	[8; 9)	[9; 10)
Giá trị đại diện	5,5	6,5	7,5	8,5	9,5
Phân xưởng A	4	5	5	4	2
Phân xưởng B	3	6	5	5	1

Đáp án là:

Cho biểu đồ mức lương của công nhân hai phân xưởng A và B (đơn vị: triệu đồng) như sau:

Hoàn thành bảng số liệu sau:

Mức lương	[5; 6)	[6; 7)	[7; 8)	[8; 9)	[9; 10)
Giá trị đại diện	5,5	6,5	7,5	8,5	9,5
Phân xưởng A	4	5	5	4	2
Phân xưởng B	3	6	5	5	1

Ta có:

Mức lương	[5; 6)	[6; 7)	[7; 8)	[8; 9)	[9; 10)
Giá trị đại diện	5,5	6,5	7,5	8,5	9,5
Phân xưởng A	4	5	5	4	2
Phân xưởng B	3	6	5	5	1

Câu 10: Thông hiểu

Xét tính đúng sai của các khẳng định

Bạn Trang thống kê chiều cao (đơn vị: cm) của các bạn học sinh nữ lớp 12C và lớp 12D ở bảng sau:

Chiều cao (cm)	[155; 160)	[160; 165)	[165; 170)	[170; 175)	[175; 180)	[180; 185)
Số học sinh nữ lớp 12C	2	7	12	3	1	1
Số học sinh nữ lớp 12D	5	9	8	2	2	0

Xét tính đúng/sai của các mệnh đề sau:

a) [NB] Giá trị đại điện của nhóm $\lbrack 165;\ 170)$ là $167,5$ . Đúng||Sai

b) [TH] Khoảng biến thiên của mẫu số liệu ghép nhóm của lớp 12D là 30. Sai|||Đúng

c) [VD, VDC] Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh nữ lớp 12C có chiều cao trung bình đồng đều hơn học sinh nữ lớp 12D. Đúng||Sai

d) [VD, VDC] Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh nữ lớp 12D có chiều cao trung bình đồng đều hơn. Sai|||Đúng

Đáp án là:

Bạn Trang thống kê chiều cao (đơn vị: cm) của các bạn học sinh nữ lớp 12C và lớp 12D ở bảng sau:

Chiều cao (cm)	[155; 160)	[160; 165)	[165; 170)	[170; 175)	[175; 180)	[180; 185)
Số học sinh nữ lớp 12C	2	7	12	3	1	1
Số học sinh nữ lớp 12D	5	9	8	2	2	0

Xét tính đúng/sai của các mệnh đề sau:

a) [NB] Giá trị đại điện của nhóm $\lbrack 165;\ 170)$ là $167,5$ . Đúng||Sai

b) [TH] Khoảng biến thiên của mẫu số liệu ghép nhóm của lớp 12D là 30. Sai|||Đúng

d) [VD, VDC] Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh nữ lớp 12D có chiều cao trung bình đồng đều hơn. Sai|||Đúng

a) Đúng

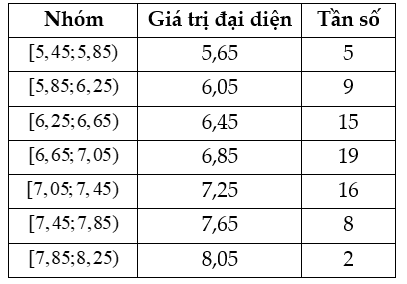
Giá trị đại điện của nhóm $\left\lbrack \mathbf{165}\mathbf{}\mathbf{;}\mathbf{\ }\mathbf{170} ight)$ là $\frac{165 + 170}{2} = 167,5$ .

b) Sai

Khoảng biến thiên của mẫu số liệu ghép nhóm của lớp 12D là $180 - 155 = 25$ .

c) Đúng

Xét mẫu số liệu của lớp 12C:

Cỡ mẫu $n_{C} = 2 + 7 + 12 + 3 + 1 + 1 = 26.$

Gọi $x_{1}\ ;\ ...\ ;\ x_{26}$ là mẫu số liệu gốc về chiều cao của các bạn học sinh nữ lớp 12C được xếp theo thứ tự không giảm.

Ta có

$x_{1}\ ;\ x_{2} \in \lbrack 155\ ;\ 160)$ ,

$x_{3}\ ;\ ...\ ;\ x_{9} \in \lbrack 160\ ;\ 165)$ ,

$x_{10}\ ;\ ...\ ;\ x_{21} \in \lbrack 165\ ;\ 170)$ ,

$x_{22}\ ;\ x_{23}\ ;x_{24} \in \lbrack 170\ ;\ 175)$ ,

$x_{25} \in \lbrack 175\ ;\ 180)$ ,

$x_{26} \in \lbrack 180\ ;\ 185)$ .

Tứ phân vị thứ nhất của mẫu số liệu gốc là $x_{7} \in \lbrack 160\ ;\ 165)$ .

Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

$Q_{1} = 160 + \frac{\frac{26}{4} - 2}{7}(165 - 160) \approx 163,214.$

Tứ phân vị thứ ba của mẫu số liệu gốc là $x_{20} \in \lbrack 165\ ;\ 170)$ .

Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:

$Q_{3} = 165 + \frac{\frac{3.26}{4} - (2 + 7)}{12}(170 - 165) = 169,375$

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

$\Delta_{C} = Q_{3} - Q_{1} \approx 169,375 - 163,214 \approx 6,161$ .

Xét mẫu số liệu của lớp 12D:

Cỡ mẫu $n_{D} = 5 + 9 + 8 + 2 + 2 + 0 = 26.$

Gọi $x_{1}\ ;\ ...\ ;\ x_{26}$ là mẫu số liệu gốc về chiều cao của các bạn học sinh nữ lớp 12D được xếp theo thứ tự không giảm.

Ta có

$x_{1}\ ;\ ...\ ;x_{5} \in \lbrack 155\ ;\ 160)$ ,

$x_{6}\ ;\ ...\ ;\ x_{14} \in \lbrack 160\ ;\ 165)$ ,

$x_{15}\ ;\ ...\ ;\ x_{22} \in \lbrack 165\ ;\ 170)$ ,

$x_{23}\ ;\ x_{24} \in \lbrack 170\ ;\ 175)$ ,

$x_{25}\ ;\ x_{26} \in \lbrack 175\ ;\ 180)$ .

Tứ phân vị thứ nhất của mẫu số liệu gốc là $x_{7} \in \lbrack 160\ ;\ 165)$ . Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: ${Q'}_{1} = 160 + \frac{\frac{26}{4} - 5}{9}(165 - 160) \approx 160,833.$

Tứ phân vị thứ ba của mẫu số liệu gốc là $x_{20} \in \lbrack 165\ ;\ 170)$ .

Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: ${Q'}_{3} = 165 + \frac{\frac{3.26}{4} - (5 + 9)}{8}(170 - 165) = 168,4375$

Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: $\Delta_{D} = {Q'}_{3} - {Q'}_{1} \approx 168,4375 - 160,833 \approx 7,6045$ .

Vì $\Delta_{C} < \Delta_{D}$ nên nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh nữ lớp 12C có chiều cao trung bình đồng đều hơn học sinh nữ lớp 12D.

d) Sai

Ta có bảng giá trị đại diện của nhóm:

Chiều cao (cm)	[155; 160)	[160; 165)	[165; 170)	[170; 175)	[175; 180)	[180; 185)
Giá trị đại diện	157,5	162,5	167,5	172,5	177,5	182,5
Số học sinh nữ lớp 12C	2	7	12	3	1	1
Số học sinh nữ lớp 12D	5	9	8	2	2	0

Xét mẫu số liệu của lớp 12C:

Số trung bình của mẫu số liệu ghép nhóm là:

${\overline{x}}_{C} = \frac{2.157,5 + 7.162,5 + 12.167,5 + 3.172,5 + 1.177,5 + 1.182,5}{26} = \frac{2170}{13}$ .

Phương sai của mẫu số liệu ghép nhóm là:

$S_{C}^{2} = \frac{1}{26}[ 2.(157,5)^{2} + 7.(162,5)^{2} + 12.(167,5)^{2}$ $+ 3.(172,5)^{2} + 1.(177,5)^{2} + 1.(182,5)^{2} ] - \left( \frac{2170}{13} ight)^{2} \approx 29,475$

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $S_{C} = \sqrt{S_{C}^{2}} = \sqrt{29,475} \approx 5,429$ .

Xét mẫu số liệu của lớp 12D:

Số trung bình của mẫu số liệu ghép nhóm là:

${\overline{x}}_{D} = \frac{5.157,5 + 9.162,5 + 8.167,5 + 2.172,5 + 2.177,5 + 0.182,5}{26} = 165$ .

Phương sai của mẫu số liệu ghép nhóm là:

$S_{D}^{2} = \frac{1}{26}[ 5.(157,5)^{2} + 9.(162,5)^{2} + 8.(167,5)^{2}$ $+ 2.(172,5)^{2} + 2.(177,5)^{2} + 0.(182,5)^{2} ]- (165)^{2} = 31,25$

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $S_{D} = \sqrt{S_{D}^{2}} = \sqrt{31,25} \approx 5,59$ .

Vì $S_{C} < S_{D}$ nên nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh nữ lớp 12C có chiều cao trung bình đồng đều hơn.

Câu 11: Thông hiểu
Tìm độ lệch chuẩn của mẫu số liệu
Thống kê tốc độ của các loại xe hơi (đơn vị: km/h) được ghi lại như sau:

Tốc độ

[42; 46)

[46; 50)

[50; 54)

[54; 58)

[58; 62)

Số xe

3

7

4

3

3

Tìm độ lệch chuẩn của mẫu số liệu ghép nhóm đã cho?
- A.
  $S = 5,286$
- B.
  $S = 5,501$
- C.
  $S = 5,154$
- D.
  $S = 5,845$
Hướng dẫn:
Ta có

Tốc độ

[42; 46)

[46; 50)

[50; 54)

[54; 58)

[58; 62)

Giá trị đại diện

44

48

52

56

60

Số xe

3

7

4

3

3

Tốc độ trung bình là:

$\overline{x} = \frac{3.44 + 7.48 + 4.52 + 3.56 + 3.60}{20} = 51,2$

Phương sai của mẫu số liệu là:

$S^{2} = \frac{1}{20}.\left( 3.44^{2} + 7.48^{2} + 4.52^{2} + 3.56^{2} + 3.60^{2} ight) - 51,2^{2} = 26,56$

Vậy độ lệch chuẩn của mẫu số liệu là: $S = \sqrt{S^{2}} \approx 5,154$
Câu 12: Vận dụng
Chọn kết luận đúng
Người ta ghi lại tiền lãi (đơn vị: triệu đồng) của một số nhà đầu tư (với số tiền đầu tư như nhau), khi đầu tư vào hai lĩnh vực $A,B$ cho kết quả như sau

Người ta có thể dùng phương sai và độ lệch chuẩn để so sánh mức độ rủi ro đầu tư các lĩnh vực có giá trị trung bình tiền lãi gần bằng nhau. Lĩnh vực nào có phương sai, độ lệch chuẩn tiền lãi cao hơn thì được coi là có độ rủi ro lớn hơn.

Theo quan điểm trên, độ rủi ro của cổ phiếu nào cao hơn?
- A.
  Lĩnh vực $A$ có độ rủi ro thấp hơn lĩnh vực $B$ .
- B.
  Không so sánh được.
- C.
  Lĩnh vực $A$ có độ rủi ro bằng lĩnh vực $B$ .
- D.
  Lĩnh vực $A$ có độ rủi ro cao hơn lĩnh vực $B$ .
Hướng dẫn:
Lĩnh vực $A$

Lĩnh vực $B$

Giá trị trung bình của hai lĩnh vực $A$ và $B$ là

${\overline{x}}_{A} = \frac{1}{25}.(2.7,5 + 5.12,5 + 8.17,5 + 6.22,5 + 4.27,5) = 18,5$

${\overline{x}}_{B} = \frac{1}{25}.(8.7,5 + 4.12,5 + 2.17,5 + 5.22,5 + 6.27,5) = 16,9$

Về độ trung bình đầu tư vào lĩnh vực $A$ lãi hơn lĩnh vực $B$ .

Độ lệch chuẩn của hai lĩnh vực $A$ và $B$ là

$s_{A} = \sqrt{\frac{1}{25}.\left( 2.7,5^{2} + 5.12,5^{2} + 8.17,5^{2} + 6.22,5^{2} + 4.27,5^{2} \right) - 18,5^{2}} = 5,8$

$s_{B} = \sqrt{\frac{1}{25}.\left( 8.7,5^{2} + 4.12,5^{2} + 2.17,5^{2} + 5.22,5^{2} + 6.27,5^{2} \right) - 16,9^{2}} = 8,04.$

Như vậy độ lệch chuẩn của mẫu số liệu thu tiền được hàng tháng khi đầu tư vào lĩnh vực $B$ cao hơn lĩnh vực $A$ nên đầu tư vào lĩnh vực $B$ rủi ro hơn.

Câu 13: Vận dụng

Chọn đáp án chính xác

Thời gian hoàn thành một bài viết chính tả của một số học sinh lớp 4 hai trường X và Y được ghi lại ở bảng sau. Gọi độ lệch chuẩn thời gian gian hoàn thành một bài viết chính tả của một số học sinh lớp 4 ở trường X và Y lần lượt là $S_{X}$ và $S_{Y}$ . Tính $S_{X} - S_{Y}$ bằng bao nhiêu?

Thời gian (Phút)	$\lbrack 6;7)$	$\lbrack 7;8)$	$\lbrack 8;9)$	$\lbrack 9;10)$	$\lbrack 10;11)$
Số học sinh trường X	8	10	13	10	9
Số học sinh trường Y	4	12	17	14	3

A.
0,53
B.
0,49
C.
0,29
D.
0,34

Hướng dẫn:

Ta lập bảng theo giá trị đại diện như sau:

Thời gian (Phút)	$\lbrack 6;7)$	$\lbrack 7;8)$	$\lbrack 8;9)$	$\lbrack 9;10)$	$\lbrack 10;11)$
Giá trị đại diện	6,5	7,5	8,5	9,5	10,5
Số học sinh trường X	8	10	13	10	9
Số học sinh trường Y	4	12	17	14	3

Cỡ mẫu $n_{X} = 8 + 10 + 13 + 10 + 9 = 50,\ \ n_{Y} = 4 + 12 + 17 + 14 + 3 = 50$ .

Thời gian trung bình hoàn thành một bài viết chính tả của học sinh trường $X$ là:

${\overline{x}}_{X} = \frac{8 \cdot 6,5 + 10 \cdot 7,5 + 13 \cdot 8,5 + 10 \cdot 9,5 + 9 \cdot 10,5}{50} = 8,54$

Phương sai của mẫu số liệu ghép nhóm của trường X là:

$S_{X}^{2} = \frac{1}{50}[ 8\cdot (6,5)^{2} + 10 \cdot (7,5)^{2}$ $+ 13 \cdot (8,5)^{2} + 10 \cdot(9,5)^{2} + 9 \cdot (10,5)^{2}] - (8,54)^{2} =1,76$

Độ lệch chuẩn của mẫu số liệu ghép nhóm của trường X là:

$S_{X} = \sqrt{S_{X}^{2}} = \sqrt{1,76} \approx 1,33$

Thời gian trung bình hoàn thành một bài viết chính tả của học sinh trường Y là:

${\overline{x}}_{Y} = \frac{4 \cdot 6,5 + 12 \cdot 7,5 + 17 \cdot 8,5 + 14 \cdot 9,5 + 3 \cdot 10,5}{50} = 8,5$

Phương sai của mẫu số liệu ghép nhóm của trường Y là:

$S_{Y}^{2} = \frac{1}{50}[ 4\cdot (6,5)^{2} + 12 \cdot (7,5)^{2} + 17 \cdot (8,5)^{2}$ $+ 14 \cdot(9,5)^{2} + 3 \cdot (10,5)^{2} ] - (8,5)^{2} =1,08$

Độ lệch chuẩn của mẫu số liệu ghép nhóm của trường Y là:

$S_{Y} = \sqrt{S_{Y}^{2}} = \sqrt{1,08} \approx 1,04$

Vậy $S_{X} - S_{Y} = 1,33 - 1,04 = 0,29$

Câu 14: Nhận biết
Chọn đáp án đúng
Một mẫu số liệu ghép nhóm có độ lệch chuẩn bằng bằng 3 thì có phương sai bằng
- A.
  $s^{2} = 6.$
- B.
  $s^{2} = 9.$
- C.
  $s^{2} = \sqrt{3}.$
- D.
  $s^{2} = 3.$
Hướng dẫn:
Phương sai: $s^{2} = 9.$
Câu 15: Nhận biết
Chọn đáp án đúng
Cho mẫu số liệu ghép nhóm thống kê có phương sai bằng là 4. Độ lệch chuẩn của mẫu số liệu ghép nhóm là:
- A.
  $2$ .
- B.
  $16$ .
- C.
  $4$ .
- D.
  $8$ .
Hướng dẫn:
Độ lệch chuẩn là: $s = \sqrt{4} = 2$ .

0/15

15 câu:

Kiểm tra Kiểm tra lại Tiếp tục Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:

Nhận biết (33%):

2/3
Thông hiểu (47%):

2/3
Vận dụng (20%):

2/3

Thời gian làm bài: 00:00:00
Số câu làm đúng: 0
Số câu làm sai: 0
Điểm số: 0
Điểm thưởng: 0

Làm lại

Chia sẻ bởi:
Bon

17 Bài viết đã được lưu

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Số điện thoại này đã được xác thực!

Bạn có thể dùng Sđt này đăng nhập tại đây!

Lỗi gửi SMS, liên hệ Admin

Sắp xếp theo

Xóa Đăng nhập để Gửi

Tìm bài trong mục này

Trắc nghiệm Toán 12 Kết nối tri thức
Trắc nghiệm Toán 12 Chân trời sáng tạo
Trắc nghiệm Toán 12 Cánh diều
Trắc nghiệm Toán 12 Sách cũ

Lớp 12
Trắc nghiệm Toán 12 Kết nối tri thức

Trắc nghiệm Toán 12 Kết nối tri thức

Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Dễ)
Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Vừa)
Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Khó)
Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Vừa)
Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Dễ)
Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Khó)

Xem thêm

111,6	134,9	130,3	134,2	140,9
109,3	154,4	156,3	116,1	96,7
105,2	80,8	80,8	110	109
139	145	161	126	114

Số giờ	[80; 98)	[98; 116)	[116; 134)	[134; 152)	[152; 170)
Giá trị đại diện	89	107	125	143	161
Số năm	3	6	3	5	3

Đối tượng	[120; 122)	[122; 124)	[124; 126)	[126; 128)	[128; 130)
Tần số	8	9	12	10	11

Cự li (m)	[19; 19,5)	[19,5; 20)	[20; 20,5)	[20,5; 21)	[21; 21,5)
Tần số	13	45	24	12	6

Tốc độ	[42; 46)	[46; 50)	[50; 54)	[54; 58)	[58; 62)
Số xe	3	7	4	3	3

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Bài tập trắc nghiệm Toán 12 KNTT Bài 10 (Mức độ Vừa)

Chúc mừng Bạn đã hoàn thành bài!

Trắc nghiệm Toán 12 Kết nối tri thức

Trắc nghiệm Toán 12 Chân trời sáng tạo

Trắc nghiệm Toán 12 Cánh diều

Trắc nghiệm Toán 12 Sách cũ

Lớp 12

Trắc nghiệm Toán 12 Kết nối tri thức

Trắc nghiệm Toán 12 Kết nối tri thức

Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Dễ)

Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Vừa)

Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Khó)

Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Vừa)

Bài tập trắc nghiệm Toán 12 KNTT Bài 19 (Mức độ Dễ)

Bài tập trắc nghiệm Toán 12 KNTT Bài 18 (Mức độ Khó)