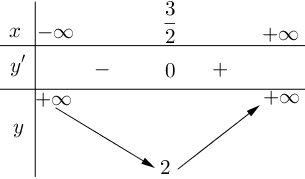
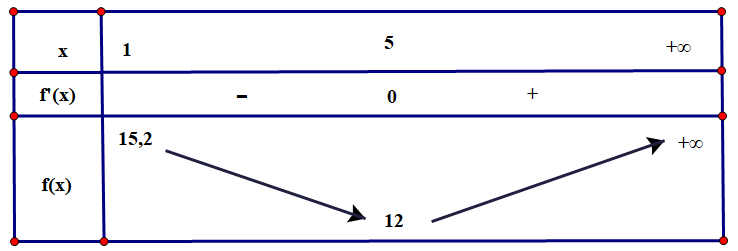
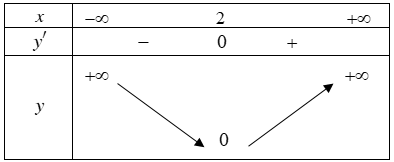
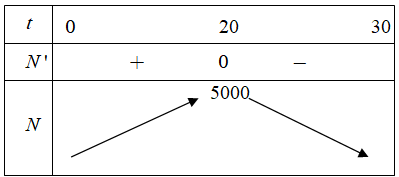
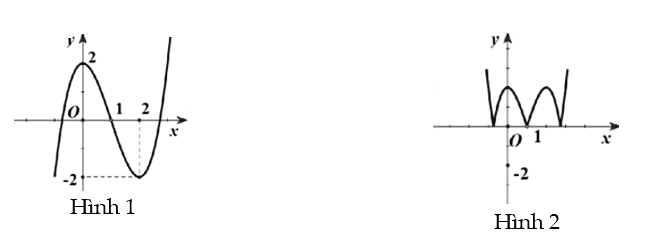Cho hàm số . Khi đó các nhận định dưới đây đúng hay sai?
a) Tập xác định của hàm số đã cho là . Sai||Đúng
b) Đồ thị của hàm số đã cho đi qua điểm . Đúng||Sai
c) Hàm số đạt cực trị tại . Sai||Đúng
d) Giá trị lớn nhất của hàm số đã cho trên đoạn bằng
. Đúng||Sai
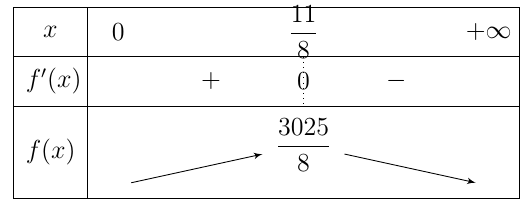
Cho hàm số . Khi đó các nhận định dưới đây đúng hay sai?
a) Tập xác định của hàm số đã cho là . Sai||Đúng
b) Đồ thị của hàm số đã cho đi qua điểm . Đúng||Sai
c) Hàm số đạt cực trị tại . Sai||Đúng
d) Giá trị lớn nhất của hàm số đã cho trên đoạn bằng
. Đúng||Sai
|
a) Sai |
b) Đúng |
c) Sai |
d) Đúng |
a) SAI vì Tập xác định của hàm số đã cho là .
b) ĐÚNG. Thay ta được
.
c) SAI. Ta có . Ta thấy
. Suy ra hàm số không đạt cực trị tại điểm
.
d) ĐÚNG. Ta có . Suy ra
.
. Vậy giá trị lớn nhất của hàm số đã cho trên đoạn
bằng
.