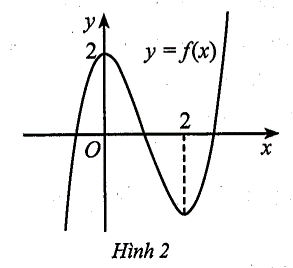
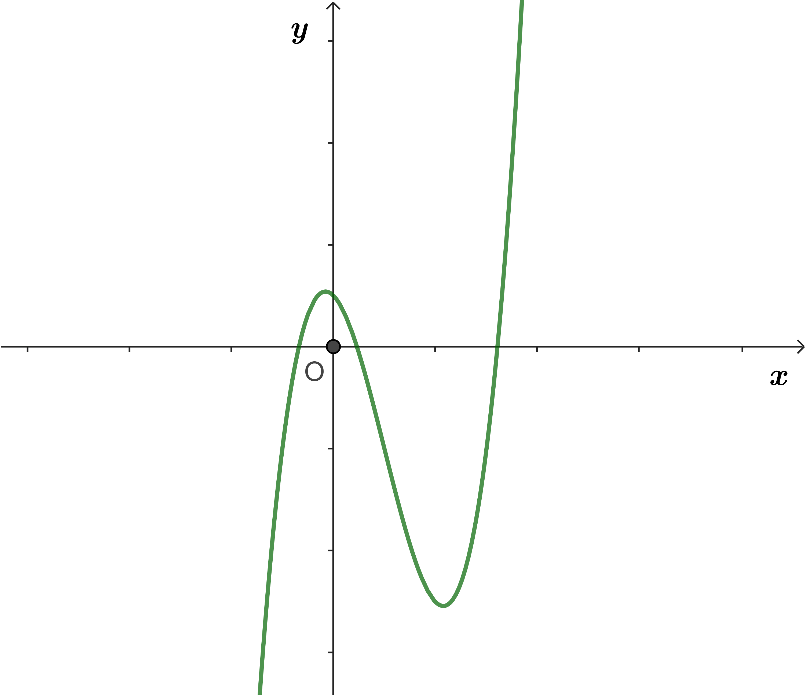
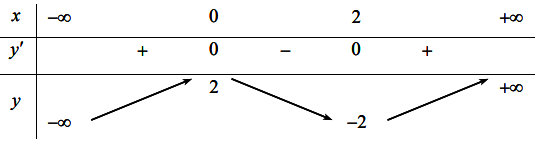Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ Đang cập nhật

Bài tập trắc nghiệm Toán 12 Cánh Diều Bài 4 (Mức độ Vừa)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Thông hiểu
    Chọn phương án đúng

    Tập tất cả các giá trị của tham số m để phương trình x^{4} - 2mx^{2} + (2m - 1) = 0 có 4 nghiệm thực phân biệt là

    Hướng dẫn:

    Xét phương trình: x^{4} - 2mx^{2} + (2m - 1) = 0.

    Đặt x^{2} = t(t \geq 0).

    Phương trình đã cho trở thành t^{2} - 2mt + (2m - 1) = 0(*).

    Để phương trình ban đầu có bốn nghiệm thực phân biệt thì phương trình (*) có hai nghiệm phân biệt dương

    \Leftrightarrow \left\{ \begin{matrix} \Delta^{'} > 0 \\ S > 0 \\ P > 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m^{2} - 2m + 1 > 0 \\ 2m > 0 \\ 2m - 1 > 0 \\ \end{matrix} ight. \Leftrightarrow \left\{ \begin{matrix} \forall m eq 1 \\ m > 0 \\ m > \frac{1}{2} \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m > \frac{1}{2} \\ m eq 1 \\ \end{matrix} ight.

    hay m \in \left( \frac{1}{2}; + \infty ight)\backslash\left\{ 1 ight\}.

  • Câu 2: Nhận biết
    Chọn đáp án đúng

    Hàm số nào dưới đây có dạng đồ thị như đường cong trong hình vẽ?

    Hướng dẫn:

    Dựa vào hình dáng đồ thị ta suy ra đồ thị của hàm số bậc 4 có hệ số a > 0.

    Vậy hàm số cần tìm là y = x^{4} - x^{2} - 1.

  • Câu 3: Thông hiểu
    Tìm m để phương trình có ba nghiệm thực

    Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình bên.

    Có bao nhiêu giá trị nguyên của tham số m để phương trình f(x) = m có ba nghiệm thực phân biệt?

    Hướng dẫn:

    Phương trình có ba nghiệm thực phân biệt \Leftrightarrow - 3 < m < 1.

    Do m nguyên nên m \in \left\{ - 2; - 1;0 ight\}

    Vậy có 3 giá trị nguyên m

  • Câu 4: Nhận biết
    Chọn phương án thích hợp

    Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình vẽ bên?

    Hướng dẫn:

    Dạng đồ thị hình bên là đồ thị hàm số trùng phương y = ax^{4} + bx^{2} + c có hệ số a < 0.

    Do đó, chỉ có đồ thị ở đáp án y = - 2x^{4} + 4x^{2} + 1 là thỏa mãn.

  • Câu 5: Thông hiểu
    Xác định tính đúng sai của từng phương án

    Cho hàm số y = f(x) liên tục trên và có đồ thị như

    Xét tính đúng sai của các khẳng định sau:

    a) Hàm số y = f(x) không có đạo hàm tại x = −2 và x = 2. Đúng||Sai

    b) Hàm số y = f(x) có ba điểm cực trị. Sai||Đúng

    c) Giá trị nhỏ nhất của hàm số y = f(x) bằng −2 đạt được tại x = 0. Đúng||Sai

    d) Hàm số y = f(x) không có giá trị lớn nhất. Sai||Đúng

    Đáp án là:

    Cho hàm số y = f(x) liên tục trên và có đồ thị như

    Xét tính đúng sai của các khẳng định sau:

    a) Hàm số y = f(x) không có đạo hàm tại x = −2 và x = 2. Đúng||Sai

    b) Hàm số y = f(x) có ba điểm cực trị. Sai||Đúng

    c) Giá trị nhỏ nhất của hàm số y = f(x) bằng −2 đạt được tại x = 0. Đúng||Sai

    d) Hàm số y = f(x) không có giá trị lớn nhất. Sai||Đúng

    a) Đúng: Hàm số y = f(x) không có đạo hàm tại x = −2 và x = 2.

    b) Sai: Hàm số y = f(x) chỉ có một điểm cực trị là x = 0.

    c) Đúng: Giá trị nhỏ nhất của hàm số y = f(x) bằng −2 đạt được tại x = 0.

    d) Sai: Ta thấy f(x) \leq 2;\forall x\mathbb{\in R}, và có xảy ra dấu bằng nên hàm số y = f(x) có giá trị lớn nhất.

  • Câu 6: Thông hiểu
    Xác định tính đúng sai của từng phương án

    Cho hàm số y = mx^{4} + (m - 1)x^{2} + 1, m là tham số thực. Xét tính đúng sai của các khẳng định sau:

    a) Hàm số có ba điểm cực trị khi và chỉ 0 < m < 1. Đúng||Sai

    b) Hàm số có hai điểm cực trị khi m = 0. Sai|| Đúng

    c) Hàm số có ba điểm cực trị khi và chỉ 0 ≤ m ≤ 1. Sai|| Đúng

    d) Hàm số có một điểm cực trị khi . Đúng||Sai

    Đáp án là:

    Cho hàm số y = mx^{4} + (m - 1)x^{2} + 1, m là tham số thực. Xét tính đúng sai của các khẳng định sau:

    a) Hàm số có ba điểm cực trị khi và chỉ 0 < m < 1. Đúng||Sai

    b) Hàm số có hai điểm cực trị khi m = 0. Sai|| Đúng

    c) Hàm số có ba điểm cực trị khi và chỉ 0 ≤ m ≤ 1. Sai|| Đúng

    d) Hàm số có một điểm cực trị khi . Đúng||Sai

    Nếu m = 0 thì hàm số đã cho trở thànhy = - x^{2} + 1.

    Đây là hàm số đa thức bậc hai nên có 1 điểm cực trị.

    Nếu m eq 0 thì hàm số đã cho là hàm số trùng phương có:

    y' = 4mx^{3} + 2(m - 1)x = 2x\left( 2mx^{2} + m - 1 ight).

    Ta có y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ 2mx^{2} + m - 1 = 0(*) \\ \end{matrix} ight.

    Hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình (∗) có hai nghiệm phân biệt khác 0.

    Điều kiện tương đương là:

    \left\{ \begin{matrix} m eq 0 \\ m(m - 1) < 0 \\ 2m.0^{2} + m - 1 eq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m eq 0 \\ 0 < m < 1 \\ m eq 1 \\ \end{matrix} ight.\ \Leftrightarrow 0 < m < 1

  • Câu 7: Thông hiểu
    Chọn khẳng định đúng

    Cho đồ thị hàm số có đồ thị như hình vẽ:

    Chọn khẳng định đúng

    Chọn khẳng định đúng?

    Hướng dẫn:

    Đồ thị hàm số có tiệm cận đứng là: x = \frac{{ - d}}{c} và tiệm cận ngang là y = \frac{a}{c} ta có:

    => \left\{ {\begin{array}{*{20}{c}} {\dfrac{{ - d}}{c} > 0} \\ {\dfrac{a}{c} > 0} \end{array}} ight. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {cd < 0} \\ {ac > 0} \end{array}} ight.

    Đồ thị hàm số cắt Ox tại \left( {\frac{{ - b}}{a};0} ight), cắt Oy tại \left( {0;\frac{b}{d}} ight)

    => \left\{ {\begin{array}{*{20}{c}} {\dfrac{{ - b}}{a} > 0} \\ {\dfrac{b}{d} > 0} \end{array}} ight. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {ab < 0} \\ {bd > 0} \end{array}} ight.

    Với a > 0 \Rightarrow b < 0;c > 0;d < 0

    Với a < 0 \Rightarrow b > 0;c < 0;d > 0

  • Câu 8: Thông hiểu
    Tìm tất cả đường thẳng thỏa mãn yêu cầu

    Cho hàm số y = \frac{3x - 2}{x} có đồ thị (C). Có tất cả bao nhiêu đường thẳng cắt (C) tại hai điểm phân biệt mà hoành độ và tung độ của giao điểm này đều là các số nguyên?

    Hướng dẫn:

    Ta có:y = 3 - \frac{2}{x}. Vì M \in (C) có tọa độ nguyên khi x \in U(2) \Rightarrow x \in \left\{ - 2; - 1;1;2 ight\}

    Các điểm thuộc (C) có tọa độ nguyên thuộc tập B = \left\{ ( - 1;5),(1;1),(2;2),( - 2;4) ight\}

    Mỗi cặp hai điểm thuộc tập B xác định một đường thẳng cắt (C) tại hai điểm có tọa độ nguyên do đó số đường thẳng cần tìm là C_{4}^{2} = 6 (đường thẳng)

  • Câu 9: Thông hiểu
    Xác định số tập con của tập S

    Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đồ thị hàm số y = x^{4} + x^{3} - 5x^{2} - x + m cắt trục hoành tại bốn điểm phân biệt có các hoành độ là x_{1},\ \ x_{2},\ \ x_{3},\ \ x_{4} thỏa mãn \left( x_{1}^{2} + 1 \right)\left( x_{2}^{2} + 1 \right)\left( x_{3}^{2} + 1 \right)\left( x_{4}^{2} + 1 \right) \geq 68.Tập Scó bao nhiêu tập con ?

    Hướng dẫn:

    Xét hàm h(x) = x^{4} + x^{3} - 5x^{2} - x + m,

    TXD:\mathbb{R},h'(x) = 4x^{3} + 3x^{2} - 10x - 1 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x \approx - 1,9 \\ x \approx 1.3 \\ x \approx - 0.09 \\ \end{matrix} ight.

    Có BBT

    Dựa vào BBT YCBT \Leftrightarrow \left\{ \begin{matrix} m + 0.05 > 0 \\ m - 4.69 < 0 \\ \end{matrix} ight.\ \Leftrightarrow - 0.05 < m < 4.69

    Khi đó

    y(x) = (x - x_{1})(x - x_{2})(x - x_{3})(x - x_{4})

    \Rightarrow y( - x) = ( - x - x_{1})( - x - x_{2})( - x - x_{3})( - x - x_{4})

    \Rightarrow y(x).y( - x) = (x^{2} - x_{1}^{2})(x^{2} - x_{2}^{2})(x^{2} - x_{3}^{2})(x^{2} - x_{4}^{2})

    \Rightarrow y(i).y( - i) = (x_{1}^{2} + 1)(x_{2}^{2} + 1)(x_{3}^{2} + 1)(x_{4}^{2} + 1)

    \Rightarrow (x_{1}^{2} + 1)(x_{2}^{2} + 1)(x_{3}^{2} + 1)(x_{4}^{2} + 1)

    = \left( i^{4} + i^{3} - 5i^{2} + m ight)\left( i^{4} - i^{3} - 5i^{2} + m ight)

    = (6 + m - 2i)(6 + m + 2i) = (6 + m)^{2} + 4 \geq 68

    \Leftrightarrow - 14 \leq m \leq 2

    Kết hợp trên ta có S = \left\{ 0;1;2 ight\}. Vậy số tập con của S là 2^{3} = 8.

  • Câu 10: Vận dụng
    Tìm giá trị của tham số a

    Có bao nhiêu giá trị nguyên âm của a để đồ thị hàm số y = x^{3} + (x + 10)x^{2} - x + 1 cắt trục hoành tại đúng một điểm?

    Hướng dẫn:

    Phương trình hoành độ giao điểm của đồ thị và trục hoành là:

    x^{3} + (a + 10)x^{2} - x + 1 = 0(*)

    \Leftrightarrow x^{3} + 10x^{2} - x + 1 = - ax^{2}

    Ta thấy x = 0 không là nghiệm của phương trình nên (*) \Leftrightarrow - \frac{x^{3} + 10x^{2} - x + 1}{x^{2}} = a

    Xét hàm số f(x) = - \frac{x^{3} + 10x^{2} - x + 1}{x^{2}};\left( \forall x\mathbb{\in R}\backslash\left\{ 0 ight\} ight)

    Ta có: f'(x) = - \frac{x^{3} + x - 2}{x^{3}} = - \frac{(x - 1)\left( x^{2} + x + 2 ight)}{x^{3}}

    f'(x) = 0 \Leftrightarrow x = 1

    Bảng biến thiên của hàm số f(x) như sau:

    Từ bảng biến thiên ta thấy đồ thị hàm số đã cho cắt trục hoành tại đúng một điểm khi (*) có đúng 1 nghiệm \Leftrightarrow a > - 11

    Vì a nguyên âm nên a \in \left\{ - 10; - 9; - 8;...; - 1 ight\}

    Vậy có 10 giá trị của a thỏa mãn yêu cầu bài toán.

  • Câu 11: Thông hiểu
    Mệnh đề nào dưới đây đúng

    Cho hàm số có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng?

    Mệnh đề nào dưới đây đúng
    Hướng dẫn:

     Ta có: \left\{ {\begin{array}{*{20}{c}} {\mathop {\lim }\limits_{x \to + \infty } y = + \infty } \\ {\mathop {\lim }\limits_{x \to - \infty } y = - \infty } \end{array}} ight. \Rightarrow a > 0

    Đồ thị hàm số cắt trục tung tại điểm có tung độ dương => d > 0

    Ta có: y' = 3a{x^2} + 2bx + c, nhận thấy hoành độ hai điểm cực trị của đồ thị hàm số có

    \left\{ {\begin{array}{*{20}{c}} {{x_1} + {x_2} = \dfrac{{ - b}}{a} > 0 \Rightarrow b < 0} \\ {{x_1}.{x_2} = \dfrac{c}{a} = 0 \Rightarrow c = 0} \end{array}} ight.

  • Câu 12: Nhận biết
    Hàm số y = f(x) là hàm số nào?

    Cho hàm số y = f(x) liên tục trên \mathbb{R} và có bảng biến thiên như hình vẽ dưới đây

    Hàm số y = f(x) là hàm số nào

    Hàm số y = f(x) là hàm số nào trong các hàm số sau:

    Hướng dẫn:

     Dựa vào bảng biến thiên ta thấy:

    \mathop {\lim }\limits_{x \to \infty } y = + \infty => Hệ số a > 0

    => Loại đáp án B và C

    Mặt khác hàm số đạt cực trị tại x = 0 và x = 2

    => Loại đáp án D

  • Câu 13: Nhận biết
    Chọn đáp án thích hợp

    Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên

    Hướng dẫn:

    Qua đồ thị là hàm bậc 3 nên loại y = x^{4} - 2x^{2} - 2, y = - x^{4} + 2x^{2} - 2

    Bên phải ngoài cùng của đồ thị đi xuống nên hệ số a < 0

    \Rightarrow Loại đáp án y = x^{3} - 3x^{2} - 2

  • Câu 14: Thông hiểu
    Xác định tính đúng sai của từng phương án

    Cho hàm số y = - x^{3} + 3x^{2} - 1. Xét tính đúng sai của các khẳng định sau:

    a) Hàm số có 2 cực trị. Đúng||Sai

    b) Điểm cực đại của hàm số là x = 2. Đúng||Sai

    c) Hàm số đồng biến trên khoảng (−1; 3).Sai||Đúng

    d) Giá trị lớn nhất của hàm số là 3. Sai||Đúng

    Đáp án là:

    Cho hàm số y = - x^{3} + 3x^{2} - 1. Xét tính đúng sai của các khẳng định sau:

    a) Hàm số có 2 cực trị. Đúng||Sai

    b) Điểm cực đại của hàm số là x = 2. Đúng||Sai

    c) Hàm số đồng biến trên khoảng (−1; 3).Sai||Đúng

    d) Giá trị lớn nhất của hàm số là 3. Sai||Đúng

    Hàm số y = - x^{3} + 3x^{2} - 1 có đồ thị như sau:

    a) Đúng. Từ đồ thị, ta khẳng định hàm số có 2 cực trị.

    b) Đúng. Từ đồ thị, ta khẳng định hàm số có điểm cực đại là x = 2.

    c) Sai. Trên khoảng (−1; 3) hàm số có đồng biến và nghịch biến.

    d) Sai. Trên R không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên

  • Câu 15: Thông hiểu
    Chọn hàm số thích hợp

    Đường cong ở hình bên là đồ thị của hàm số y = \frac{ax + b}{cx + d} với a,b,c,d là các số thực. Mệnh đề nào dưới đây đúng?

    Hướng dẫn:

    Dựa vào đồ thị ta nhận thấy tiệm cận đứng bằng 2, hàm số nghịch biến vậy chọn B

  • Câu 16: Thông hiểu
    Chọn đáp án đúng

    Cho hàm số y = f(x) là hàm phân thức bậc nhất chia bậc nhất và có đồ thị như hình Svẽ bên. Số nghiệm của phương trình f(x) = 2024 là

    Hướng dẫn:

    Số nghiệm của phương trình f(x) = 2024 bằng số giao điểm của đồ thị hàm số y = f(x)với đường thẳng y = 2024.

    Dựa vào đồ thị hàm số y = f(x) suy ra số nghiệm của phương trình là 1.

  • Câu 17: Thông hiểu
    Khẳng định nào sau đây là sai

    Cho hàm số có bảng biến thiên như hình vẽ:

    Khẳng định nào sau đây là sai

    Khẳng định nào sau đây là sai?

    Hướng dẫn:

    Dựa vào bảng biến thiên suy ra hàm số đã cho có hai điểm cực đại và một điểm cực tiểu

    Giá trị lớn nhất của hàm số trên tập số thực bằng 4

    Hàm số có ba cực trị nên ab < 0 mà c = 0 => ab\left( {c + 1} ight) < 0

  • Câu 18: Thông hiểu
    Xác định số giao điểm theo yêu cầu

    Số giao điểm của đồ thị hàm số y = - x^{3} + 3x với trục hoành là

    Hướng dẫn:

    Xét phương trình hoành dộ giao điểm - x^{3} + 3x = 0

    \Leftrightarrow x( - x^{2} + 3) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = \pm \sqrt{3} \\ \end{matrix} ight..

    Vậy có 3 giao điểm.

  • Câu 19: Thông hiểu
    Xét tính đúng sai của các nhận định

    Cho hàm số y = f(x) có đạo hàm trên \mathbb{R} và đồ thị như Hình 3.

    Các nhận định sau đúng hay sai?

    a) Hàm số nghịch biến trên khoảng ( - \infty; - 1). Đúng||Sai

    b) Hàm số đạt cực tiểu tại điểm x_{0} = - 1. Đúng||Sai

    c) Đạo hàm của hàm số nhận giá trị không âm trên khoảng ( - 1;1). Đúng||Sai

    d) Giá trị lớn nhất của hàm số trên đoạn \lbrack - 1;0\rbrack bằng 1. Sai||Đúng

    Đáp án là:

    Cho hàm số y = f(x) có đạo hàm trên \mathbb{R} và đồ thị như Hình 3.

    Các nhận định sau đúng hay sai?

    a) Hàm số nghịch biến trên khoảng ( - \infty; - 1). Đúng||Sai

    b) Hàm số đạt cực tiểu tại điểm x_{0} = - 1. Đúng||Sai

    c) Đạo hàm của hàm số nhận giá trị không âm trên khoảng ( - 1;1). Đúng||Sai

    d) Giá trị lớn nhất của hàm số trên đoạn \lbrack - 1;0\rbrack bằng 1. Sai||Đúng

    Theo Hình 3, hàm số nghịch biến trên khoảng ( - \infty\ ;\ - 1) và đạt cực tiểu tại điểm x_{o} = - 1.

    Vì hàm số đồng biến trên khoảng ( - 1\ \ ;\ 1) nên đạo hàm của hàm số nhận giá trị không âm trên khoảng đó. Giá trị lớn nhất của hàm số trên đoạn \lbrack - 1\ ;\ 0\rbrack bằng - 1.

    Đáp án: a) Đúng, b) Đúng, c) Đúng, d) Sai.

  • Câu 20: Vận dụng
    Xác định số cặp điểm thỏa mãn yêu cầu

    Cho hàm số y = x^{3} + x^{2} - 4 có đồ thị (C). Hỏi có bao nhiêu cặp điểm A;B \in (C) sao cho ba điểm O;A;B thẳng hàng và OA - 2OB = 0 với O là gốc tọa độ?

    Hướng dẫn:

    Gọi d là đường thẳng đi qua ba điểm O, A, B khi đó d có phương trình y = k.x

    Khi đó hoành độ của O, A, B là nghiệm của phương trình x^{3} + x^{2} - 4 = kx

    Giả sử A\left( x_{1};kx_{1} ight),B\left( x_{2};kx_{2} ight) khi đó ta có: \left\{ \begin{matrix} {x_{1}}^{3} + {x_{1}}^{2} - 4 = kx_{1} \\ {x_{2}}^{3} + {x_{2}}^{2} - 4 = kx_{2} \\ \end{matrix} ight.

    Do OA - 2OB = 0 nên \overrightarrow{OA} = \pm 2\overrightarrow{OB} \Rightarrow x_{1} = \pm 2kx_{2}

    TH1: x_{1} = 2kx_{2} \Rightarrow \left\{ \begin{matrix} 8{x_{2}}^{3} + 4{x_{2}}^{2} - 4 = 2kx_{2} \\ {x_{2}}^{3} + {x_{2}}^{2} - 4 = kx_{2} \\ \end{matrix} ight.

    \Rightarrow 6{x_{2}}^{3} + 2{x_{2}}^{2} + 4 = 0 \Rightarrow x_{2} = - 1

    Khi đó A( - 2; - 8),B( - 1; - 4).

    TH2: x_{1} = - 2kx_{2} \Rightarrow \left\{ \begin{matrix} - 8{x_{2}}^{3} + 4{x_{2}}^{2} - 4 = - 2kx_{2} \\ {x_{2}}^{3} + {x_{2}}^{2} - 4 = kx_{2} \\ \end{matrix} ight.

    \Rightarrow - 6{x_{2}}^{3} + 6{x_{2}}^{2} - 12 = 0 \Rightarrow x_{2} = - 1

    Khi đó A(2;8),B( - 1; - 4).

    Vậy có 2 cặp A; B thỏa mãn.

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (20%):
    2/3
  • Thông hiểu (70%):
    2/3
  • Vận dụng (10%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Tải file làm trên giấy
1
43 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này