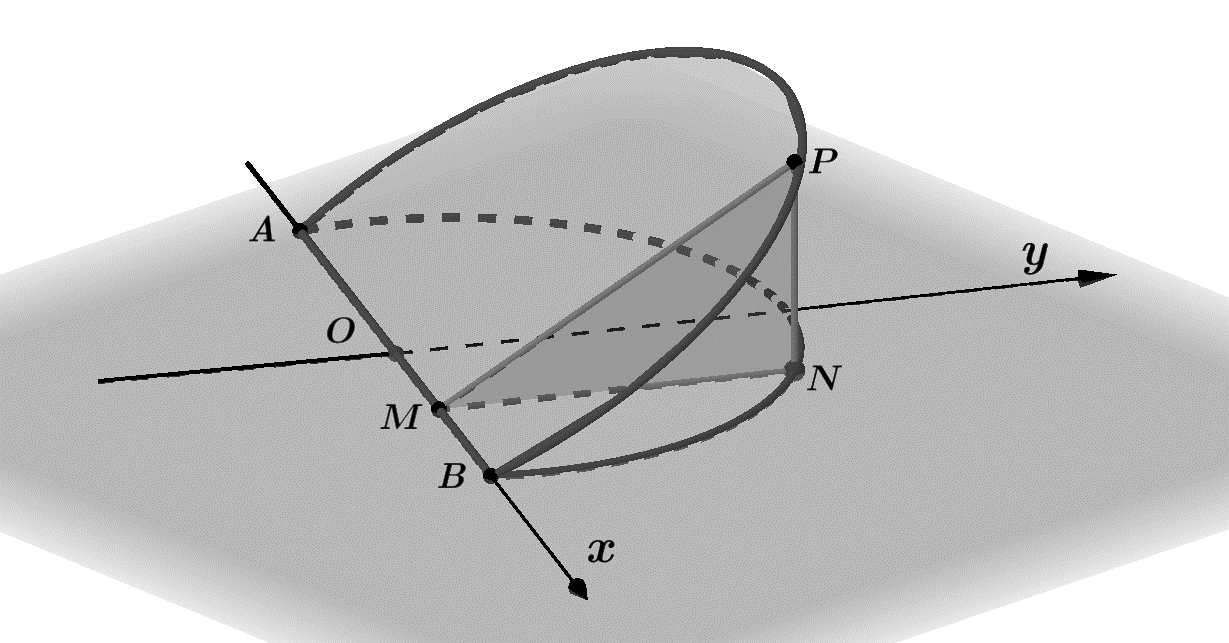
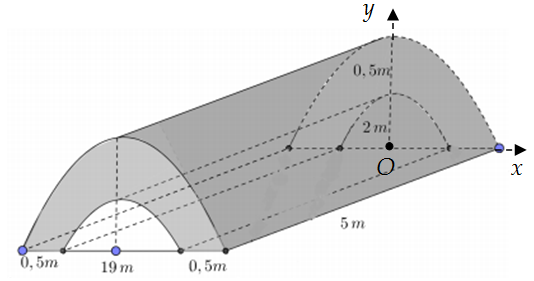
Một chi tiết máy được thiết kế như hình vẽ bên.

Các tứ giác là các hình vuông cạnh
. Tứ giác
là hình chữ nhật có
. Mặt bên
được mài nhẵn theo đường parabol
có đỉnh parabol nằm trên cạnh
. Tính thể tích của chi tiết máy gần nhất với giá trị nào dưới đây?

Gọi hình chiếu của trên
và
là
và
.
Vật thể được chia thành hình lập phương có cạnh
, thể tích
và phần còn lại có thể tích
.
Khi đó thể tích vật thể .
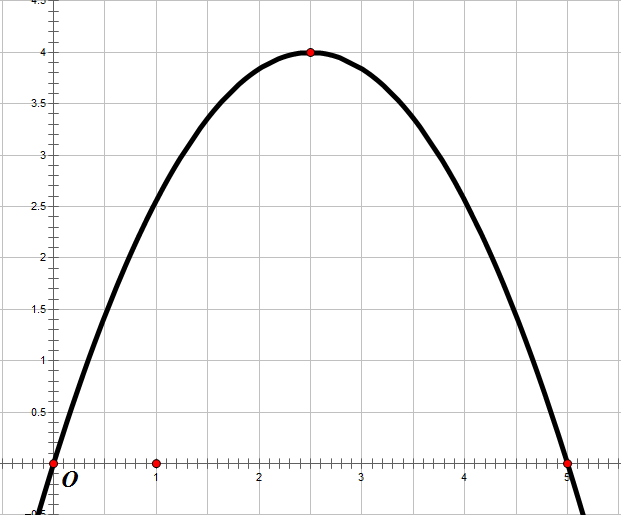
Đặt hệ trục sao cho
trùng với
,
trùng với
,
trùng với tia
song song với
.
Khi đó Parabol có phương trình dạng
, đi qua điểm
do đó
.
Cắt vật thể bởi mặt phẳng vuông góc với và đi qua điểm
ta được thiết diện là hình chữ nhật
có cạnh là
và
Do đó diện tích
Áp dụng công thức thể tích vật thể ta có .
Từ đó



 .
.