Tìm tất cả các giá trị thực của tham số để đồ thị hàm số
có đúng một tiệm cận đứng.
Để đồ thị hàm số có đúng một tiệm cận đứng
có nghiệm duy nhất
.
Tìm tất cả các giá trị thực của tham số để đồ thị hàm số
có đúng một tiệm cận đứng.
Để đồ thị hàm số có đúng một tiệm cận đứng
có nghiệm duy nhất
.
Cho hàm số có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
Hàm số có tập xác định:
Ta có:
Không tồn tại tiệm cận ngang khi
vậy hàm số
có tiệm cận ngang
;
Đồ thị hàm số có tiệm cận đứng
Vậy tổng số tiệm cận đứng và ngang là 2.
Cho hàm số có bảng biến thiên như sau:
Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận?
Từ bảng biến thiên, ta có:
là TCN;
là TCĐ;
là TCĐ.
Vậy đồ thị hàm số đã cho có đúng ba đường tiệm cận
Giá trị của tham số m để đồ thị hàm số có đường tiệm cận ngang
là:
Để tồn tại các đường tiệm cận của đồ thị hàm số thì
Khi đó phương trình đường tiệm cận ngang là
Điều kiện để đồ thị hàm số có tiệm cận là:
luôn đúng với
Phương trình đường tiệm cận ngang là nên ta có
Cho hàm số . Tìm
để khoảng cách từ gốc
đến tiệm cận xiên hoặc ngang là nhỏ nhất.
Cho hàm số . Tìm
để khoảng cách từ gốc
đến tiệm cận xiên hoặc ngang là nhỏ nhất.
Tìm tất cả các giá trị thực của tham số để đồ thị hàm số
nhận đường thẳng
làm tiệm cận ngang.
Ta có là TCN.
Do đó theo yêu cầu bài toán .
Cho hàm số có bảng biến thiên như sau:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số là:
Điều kiện xác định của hàm số là
Từ bảng biến thiên ta có:
Tập xác định
Ta có:
suy ra đồ thị hàm số có tiệm cận ngang
.
suy ra đồ thị hàm số có tiệm cận ngang
.
suy ra đồ thị hàm số có tiệm cận đứng
.
suy ra đồ thị hàm số có tiệm cận đứng
.
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
.
Biết đồ thị hàm số nhận trục hoành và trục tung làm hai tiệm cận. Giá trị m + n là:
Điều kiện để đồ thị hàm số có tiệm cận ngang là bậc f(x) không lớn hơn bậc của g(x).
Điều kiện để đường thẳng x = x0 là tiệm cận đứng của đồ thị hàm số là x0 là nghiệm của g(x) nhưng không là nghiệm của f(x) hoặc x0 là nghiệm bội n của g(x) đồng thời là nghiệm bội m của f(x) và m < n
Điều kiện
Phương trình đường tiệm cận ngang của đồ thị hàm số là
=>
Đặt
Nhận thấy với mọi m, n nên đồ thị nhận trục tung x = 0 làm tiệm cận đứng thì g(0) = 0
=> n – 6 = 0 => n = 6
Kết hợp với (*) => m = 3
Vậy m + n = 9
Tập hợp tất cả các giá trị thực của tham số để đồ thị hàm số
có đúng hai tiệm cận đứng?
Điều kiện xác định
Vì nên để đồ thị hàm số có đúng hai tiệm cận đứng thì phương trình
phải có hai nghiệm phân biệt lớn hơn
.
Xét hàm số trên
có:
Bảng biến thiên
Phương trình (*) có hai nghiệm phân biệt lớn hơn khi
.
Vậy đáp án cần tìm là .
Cho hàm số y = f(x) là hàm số bậc 2. Đồ thị hàm số y = f’(x) như hình vẽ dưới đây và f(-1) < 20
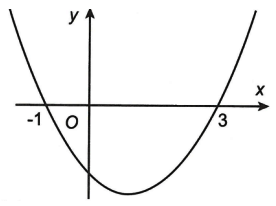
Đồ thị hàm số (m là tham số thực) có bốn tiệm cận khi và chỉ khi:
Điều kiện
Từ đồ thị hàm số f’(x) ta có bảng biến thiên hàm số f(x) là:

Nếu m = 20 thì đồ thị hàm số không có đủ bốn tiệm cận
Nếu thì
=> y = 1 là tiệm cận ngang của đồ thị hàm số
Ta có phương trình f(x) = 20 có một nghiệm x = a > 3 vì f(-1) < 20
=> Đồ thị hàm số g(x) có bốn tiệm cận khi phương trình f(x) = m có ba nghiệm phân biệt khác a
=> f(3) < m < f(-1)
Cho hàm số . Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
Tập xác định
Ta có:
Vậy đồ thị có một tiệm cận ngang .
ho hàm số . Khẳng định nào sau đây là khẳng định đúng?
Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng y = y0 là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đồ thị hàm số có hai đường tiệm cận đứng là x = 1 và x = -1 và một tiệm cận ngang là y = -1
Cho hàm số . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có hai tiệm cận đứng.
Ta có:
Đồ thị hàm số có hai tiệm cận đứng khi và chỉ khi phương trình có hai nghiệm phân biệt thỏa mãn
Cho hàm số có bảng biến thiên như hình vẽ dưới đây.
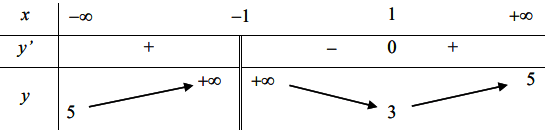
Số đường tiệm cận của đồ thị hàm số là:
Đường thẳng là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Đường thẳng là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số
nếu ít nhất một trong các điều kiện sau được thỏa mãn:
Phương trình có 2 nghiệm phân biệt
=> Đồ thị hàm số có 2 đường tiệm cận đứng.
Khi thì
Khi thì
Vậy đồ thị hàm số có 1 tiệm cận ngang.
Cho hàm số bậc ba có đồ thị như hình vẽ dưới đây.
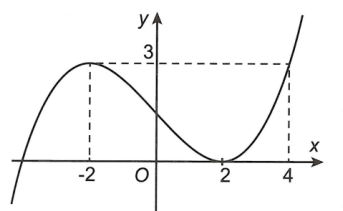
Đồ thị hàm số có bao nhiêu đường tiệm cận đứng và tiệm cận ngang.
Đặt khi đó
thì
Khi đó
=> y = 0 là tiệm cận ngang của đồ thị hàm số g(x)
Mặt khác
=> Đồ thị hàm số g(x) có ba đường tiệm cận đứng.
Vậy đồ thị hàm số g(x) có bốn đường tiệm cận.
Tìm giá trị thực của tham số để đồ thị hàm sô
có đường tiệm cận đứng đi qua điểm
TXĐ: .
Ta có là TCĐ.
Do đó yêu cầu bài toán .
Tìm tất cả các đường tiệm cận của đồ thị hàm số
TXĐ: suy ra đồ thị không có tiệm cận đứng.
Ta có:
là TCN
là TCN.
Tìm tất cả các giá trị thực của tham số để đồ thị hàm số
có đúng một tiệm cận ngang và đúng một tiệm cận đứng.
Ta có là tiệm cận ngang với mọi
Để đồ thị hàm số có đúng một tiệm cận ngang và đúng một tiệm cận đứng
Phương trình
có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có một nghiệm bằng
Đường thẳng y = kx + m vừa là tiếp tuyến của đường cong , vừa cắt hai trục toạ độ A, B sao cho tam giác OAB cân tại gốc tạo độ O. Tính giá trị của biểu thức S = m + k
Đồ thị hàm số có bao nhiêu đường tiệm cận ngang?
Ta có:
*
*
Vậy đồ thị có một đường tiệm cận ngang là .
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

