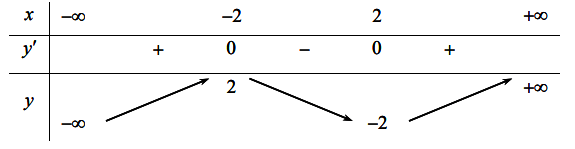Tìm tập hợp tất cả các giá trị của tham số để đồ thị hai hàm số
và
cắt nhau tại
điểm phân biệt?
Xét phương trình hoành độ giao điểm:
Điều kiện:
Ta có:
Xét hàm số trên
Nhận thấy, hàm số liên tục trên các khoảng
Ta có,
với
Suy ra, hàm số đồng biến trên
.
Bảng biến thiên
Từ bảng biến thiên ta suy ra đồ thị hai hàm số và
cắt nhau tại
điểm phân biệt khi
.