Cho ba điểm . Tìm tập hợp các điểm
thỏa mãn
Theo bài ra ta có:
Mặt cầu:
Cho ba điểm . Tìm tập hợp các điểm
thỏa mãn
Theo bài ra ta có:
Mặt cầu:
Cho mặt phẳng và hai đường thẳng
,
. Mặt cầu
có tâm thuộc
, tiếp xúc với
và mặt phẳng
, có phương trình:
Ta có:
;
đi qua điểm
và có vectơ chỉ phương
.
Giả sử là tâm và
là bán kính của mặt cầu
.
Ta có:
.
tiếp xúc với
và
.
Với
,
.
Với
.
Cho hai mặt phẳng ,
có phương trình
và
Mặt cầu có tâm nằm trên mặt phẳng
và tiếp xúc với mặt phẳng
tại điểm
, biết rằng
thuộc mặt phẳng
và có hoành độ
, có phương trình là:
Vì và có hoành độ bằng 1 nên
.
Lại có, mặt cầu tiếp xúc với mặt phẳng nên
.
Gọi là tâm của mặt cầu
cần tìm.
Ta có tiếp xúc với mp
tại M nên
.
Mặt phẳng có vectơ pháp tuyến
.
Ta có:
Bán kính mặt cầu
Vậy phương trình mặt cầu .
Cho tứ diện ABCD có Tìm tập hợp các điểm M thỏa mãn
Ta có:
Mặt cầu
Trong không gian , cho ba điểm
, điểm
thay đổi trên mặt phẳng
,
là điểm trên tia
sao cho
. Biết khi M thay đổi thì điểm N luôn nằm trên mặt cầu cố định. Tính bán kính mặt cầu đó
Giả sử .
Do O, M, N thẳng hàng và N thuộc tia ON nên suy ra:
Do
Vậy thuộc mặt cầu cố định bán kính
.
Trong không gian cho đường tròn
Bán kính r của đường tròn (C) bằng:
Cùng đề trên nên có bán kính mặt cầu là .
Khoảng cách từ I đến thiết diện là .
Bán kính của
là:
Trong không gian tọa độ cho mặt cầu
và đường thẳng
là giao tuyến của hai mặt phẳng
và
. Đường thẳng
cắt mặt cầu
tại hai điểm phân biệt
thỏa mãn
khi:
Ta có .
Phương trình tham số của là
.
.
(*).
(*) .
Phương trình (*) có hai nghiệm phân biệt khi .
Khi đó .
.
.
Suy ra
.
Cách 2:
Mặt cầu có tâm
,
,
.
Đường thẳng qua
, có VTCP
Yêu cầu đề bài tương đương .
Viết phương trình mặt cầu (S) qua gốc O và các giao điểm của mặt phẳng với ba trục tọa độ.
cắt ba trục
tại
nên:
Vậy
Cho hình lập phương có cạnh bằng 1 có
trùng với ba trục
. Viết phương trình mặt cầu
tiếp xúc với tất cả các cạnh của hình lập phương.
tiếp xúc với 12 cạnh của hình lập phương tại trung điểm của mỗi cạnh.
Tâm là trung điểm chng của 6 đoạn nối trung điểm của các cặp cạnh đối diện đôi một có độ dài bằng
Bán kính
Cho hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên bằng
. Gọi h là chiều cao của khối chóp và R là bán kính mặt cầu ngoại tiếp khối chóp. Tỉ số
bằng:

Gọi O là tâm , suy ra
và
Trong SOA, ta có
Trong mặt phẳng SOA, kẻ trung trực d của đoạn SA cắt SO tại I, suy ra:
Do đó nên I là tâm mặt cầu ngoại tiếp khối chóp .
Gọi M là tung điểm SA, ta có nên
Vậy
Trong không gian với hệ tọa độ , cho điểm
. Mặt phẳng
đi qua
và cắt các trục
lần lượt tại các điểm
sao cho
là trực tâm của
. Tính diện tích mặt cầu ngoại tiếp tứ diện
?
Gọi lần lượt thuộc các trục tọa độ Ox, Oy, Oz.
Khi đó ta có phương trình mặt phẳng (α) đi qua các điểm A, B, C là
Vì
Ta có:
Theo đề bài ta có H là trực tâm , ta có:
thay vào (1) ta được:
. Gọi
là tâm mặt cầu ngoại tiếp chóp tứ giác OABC, ta có:
Vậy
Trong không gian với hệ trục tọa độ , cho mặt cầu
có bán kính
đường thẳng
và mặt phẳng
Trong các số
theo thứ tự dưới đây, số nào thỏa mãn
đồng thời tâm
của
thuộc đường thẳng
và
tiếp xúc mặt phẳng
?
Ta có
Do tiếp xúc với
nên
Mặt khác có tâm
; bán kính
Xét khi
Do nên ta loại trường hợp này
Xét khi
Do nên thỏa mãn.
Cho hình chóp có đáy ABC là tam giác vuông cân tại B, . Cạnh bên , hình chiếu của điểm S lên mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Bán kính mặt cầu ngoại tiếp khối chóp
là:

Gọi M là trung điểm AC, suy ra
Tam giác SAC có SM là đường cao và cũng là trung tuyến nên tam giác SAC cân tại S.
Ta có , suy ra tam giác SAC đều.
Gọi G là trọng tâm , suy ra
. (1)
Tam giác ABC vuông tại B, có M là trung điểm cạnh huyền AC nên M là tâm đường tròn ngoại tiếp tam giác ABC.
Lại có nên SM là trục của tam giác ABC.
Mà G thuộc SM nên suy ra .
Từ (1) và (2), suy ra hay G là tâm mặt cầu ngoại tiếp khối chóp
.
Bán kính mặt cầu .
Cho tứ diện ABCD có . Viết phương trình mặt cầu
nội tiếp tứ diện.
Ta có:
Tứ diện ABCD đều.
tiếp xúc với bốn mặt của tứ diện tại trọng tâm của mỗi mặt.
Trọng tâm G của tam giác đều ACD: tâm của
Bán kính của
Trong không gian với hệ tọa độ , cho hai điểm
và
. Có tất cả bao nhiêu giá trị thực của tham số m để phương trình
là phương trình của một mặt cầu (S) sao cho qua hai điểm
có duy nhất một mặt phẳng cắt mặt cầu (S) đó theo giao tuyến là một đường tròn có bán kính bằng 1.
Ta có:
Suy ra (*) là phương trình mặt cầu
Khi đó, mặt cầu (S) có tâm và bán kính
Gọi (P) là mặt phẳng đi qua A, B.
Theo giả thiết (P) cắt mặt cầu (S) theo giao tuyến là đường tròn có bán kính r = 1.
Mặt khác, khoảng cách từ tâm I đến mặt phẳng (P) là
Ta có: suy ra
là một vectơ chỉ phương của đường thẳng
Suy ra đường thẳng là:
Để có duy nhất mặt phẳng (P) thỏa mãn bài thì
TH1. Mặt phẳng (P) đi qua điểm I và
Ta có
+ Với (loại).
+ Với m = −2 ⇒ ⇒ m = −2 (thỏa mãn).
TH2. Mặt phẳng (P) cách I một khoảng lớn nhất ⇔ d lớn nhất ⇔ d = d(I, AB). (*)
Khi đó
Vậy có 2 giá trị tham số m thỏa mãn yêu cầu.
Trong không gian , cho 3 điểm
và
. Gọi
là mặt cầu tâm A bán kính bằng 3 và
là mặt cầu tâm B bán kính bằng 6. Hỏi có tất cả bao nhiêu mặt phẳng đi qua C và tiếp xúc đồng thời với cả hai mặt cầu
?
Phương trình mặt phẳng qua C có dạng .
Mặt phẳng tiếp xúc
ta có
(1)
Mặt phẳng tiếp xúc
ta có
(2)
Từ đây ta có phương trình
Từ (1), (3) ta có:
Trường hợp này ta tìm được hai mặt phẳng:
Từ (1); (4) ta có:
Trường hợp này không có mặt phẳng nào.
Trong không gian với hệ trục tọa độ Oxyz, xét mặt cầu (S) đi qua hai điểm và có tâm thuộc mặt phẳng
bán kính của mặt cầu (S) có giá trị nhỏ nhất là
Hình vẽ minh họa
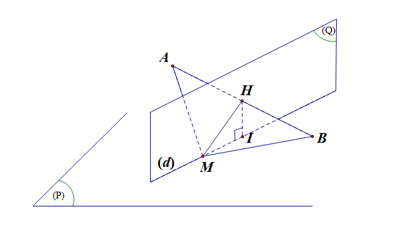
Gọi H là trung điểm của đoạn thẳng AB nên H(2; 3; 1). Vecto .
Mặt cầu đi qua A, B có tâm M thuộc mặt phẳng (Q)
là mặt phẳng trung trực của đoạn thẳng AB
qua H và có vecto pháp tuyến có phương trình
.
Do tâm M của mặt cầu cũng thuộc (P) nên M thuộc đường thẳng (d) là giao của (P) và (Q) có vectơ chỉ phương và qua
.
Gọi d là khoảng cách từ H đến (d), ,
.
Ta có . Nhận thấy HB không đổi, R nhỏ nhất khi MH nhỏ nhất, MH nhỏ nhất khi M trùng I, lúc đó
. (I là hình chiếu vuông góc của H lên (d))
Vậy .
Phương trình mặt cầu có tâm và tiếp xúc trục Oz là:
Gọi H là hình chiếu của trên Oz
.
Vậy phương trình mặt cầu là:
Phương trình mặt cầu tâm nào sau đây tiếp xúc với trục Ox:
Mặt cầu tâm , bán kính R và tiếp xúc trục Ox
.
Vậy
Lưu ý : Học sinh hoàn toàn có thể sử dụng công thức khoảng cách từ một điểm đến một đường thẳng để giải quyết.
Trong không gian với hệ tọa độ , cho hai điểm
và
. Hai điểm
thay đổi sao cho
và
. Biết rằng luôn tồn tại một mặt cầu cố định đi qua
và tiếp xúc với mặt phẳng
. Bán kính của mặt cầu đó là:
Phương trình mặt phẳng là
.
Gọi và
là tâm và bán kính của mặt cầu cố định.
Ta có
Mà không đổi nên
, hay
.
Mặt khác ta có .
Vậy .
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

