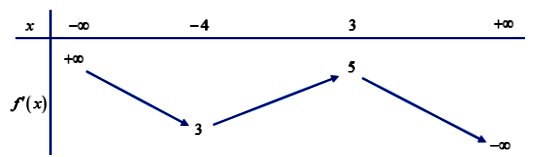
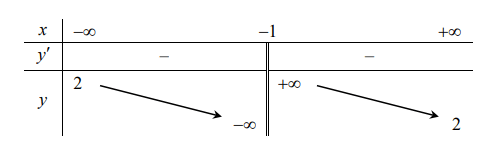
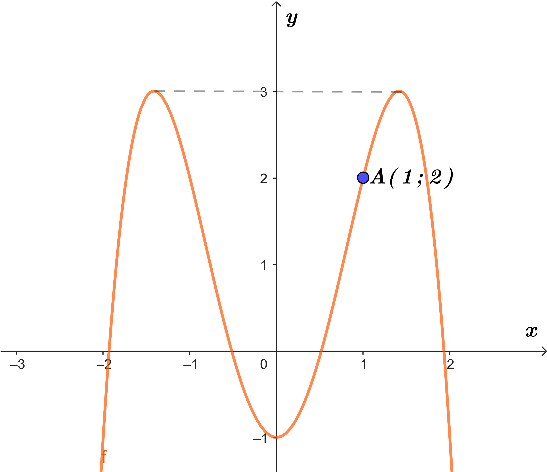
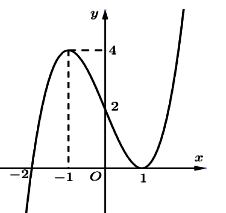
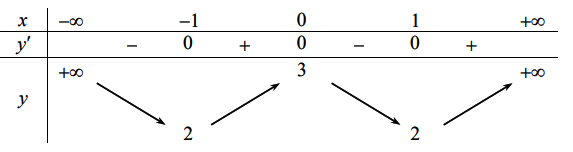Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Trắc nghiệm Toán 12 Kết nối tri thức
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập trắc nghiệm Toán 12 KNTT Bài 4 (Mức độ Khó)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Vận dụng cao
    Xác định tất cả giá trị nguyên tham số m thỏa mãn điều kiện

    Cho hàm số f(x) = x^{3} + x + 2. Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình f\left( \sqrt[3]{f^{3}(x) + f(x) + m} \right) = - x^{3} - x + 2 có nghiệm x \in \lbrack - 1;2\rbrack?

    Hướng dẫn:

    Xét hàm số f(t) = t^{3} + t + 2, ta có f'(t) = 3t^{2} + 1 > 0,\forall t\mathbb{\in R}.

    Do đó hàm số f đồng biến trên \mathbb{R}.

    Ta có f\left( \sqrt[3]{f^{3}(x) + f(x) + m} ight) = f( - x)

    \Leftrightarrow - x = \sqrt[3]{f^{3}(x) + f(x) + m} \Leftrightarrow f^{3}(x) + f(x) + x^{3} + m = 0\ \ \ \ \ \ (1)

    Xét h(x) = f^{3}(x) + f(x) + x^{3} + m trên đoạn \lbrack - 1;2brack.

    Ta có h'(x) = 3f'(x) \cdot f^{2}(x) + f'(x) + 3x^{2}

    = f'(x)\left\lbrack 3f^{2}(x) + 1 ightbrack + 3x^{2}.

    Ta có f'(x) = 3x^{2} + 1 > 0,\forall x \in \lbrack - 1;2brack \Rightarrow h'(x) > 0,\forall x \in \lbrack - 1;2brack.

    Hàm số h(x) đồng biến trên \lbrack - 1;2brack nên \min_{\lbrack - 1;2brack}h(x) = h( - 1) = m - 1,\max_{\lbrack - 1;2brack}h(x) = h(2) = m +1748.

    Phương trình (1) có nghiệm khi và chỉ khi

    \begin{matrix} \mathop {\min }\limits_{[ - 1;2]} h\left( x ight) \cdot \mathop {\max }\limits_{[ - 1;2]} h\left( x ight) \leqslant 0 \Leftrightarrow h\left( { - 1} ight) \cdot h\left( 2 ight) \hfill \\ \Leftrightarrow \left( {m - 1} ight)\left( {1748 + m} ight) \leqslant 0 \hfill \\ \Leftrightarrow - 1748 \leqslant m \leqslant 1. \hfill \\ \end{matrix}

    Do m nguyên nên tập các giá trị m thỏa mãn là S = \{ - 1748; - 1747;\ldots;0;1\}.

    Vậy có tất cả 1750 giá trị nguyên của m thỏa mãn.

  • Câu 2: Vận dụng cao
    Chọn đáp án đúng

    Cho hàm số y = x^{4} - 2x^{2} có đồ thị (C), có bao nhiêu đường thẳng dcó đúng 3 điểm chung với đồ thị (C) và các điểm chung có hoành độ x_{1},x_{2},x_{3} thỏa mãn\ {x_{1}}^{3} + {x_{2}}^{3} + {x_{3}}^{3} = - 1.

    Hướng dẫn:

    Vì đường thẳng d cắt đồ thị hàm số (C) tại 3 điểm phân biệt nên đường thẳng dlà đường thẳng có hệ số góc dạng y = ax + b.

    Phương trình hoành độ giao điểm của d và (C) là: x^{4} - 2x^{2} = ax + b.

    Mà phương trình là phương trình bậc 4 nên phương trình muốn có 3 nghiệm phân biệt thì trong đó sẽ có 1 nghiệm kép gọi là x_{1}, hai nghiệm còn lại là x_{2},x_{3}.

    Suy ra đường thẳng dlà tiếp tuyến của đồ thị (C), không mất tính tổng quát giả sử đường thẳng dtiếp xúc với đồ thị hàm số (C)tại x_{1}.

    Gọi dlà tiếp tuyến của (C)tại điểm có hoành độ x_{1}, d cắt (C) tại 2 điểm phân biệt có hoành độ x_{2},x_{3}( eq x_{1}) thỏa mãn {x_{1}}^{3} + {x_{2}}^{3} + {x_{3}}^{3} = - 1.

    Ta có: d:y = (4{x_{1}}^{3} - 4x_{1})(x - x_{1}) + {x_{1}}^{4} - 2{x_{1}}^{2}.

    Phương trình hoành độ giao điểm của dvà (C)là:

    x^{4} - 2x^{2} = (4{x_{1}}^{3} - 4x_{1})(x - x_{1}) + {x_{1}}^{4} - 2{x_{1}}^{2}(1)

    Yêu cầu bài toán \Leftrightarrow (1) có 3 nghiệm phân biệt thỏa mãn {x_{1}}^{3} + {x_{2}}^{3} + {x_{3}}^{3} = - 1.

    (1) \Leftrightarrow (x - x_{1})^{2}(x^{2} + 2x_{1}x + 3{x_{1}}^{2} - 2) = 0\Leftrightarrow \left\{ \begin{matrix} x = x_{1} \\ f(x) = x^{2} + 2x_{1}x + 3{x_{1}}^{2} - 2 = 0 \\ \end{matrix} ight.

    Để phương trình (1) có 3 nghiệm phân biệt thỏa mãn {x_{1}}^{3} + {x_{2}}^{3} + {x_{3}}^{3} = - 1thì phương trình f(x) = 0 phải có 2 nghiệm phân biệt x_{2},x_{3} khác x_{1}và thỏa mãn định lí Vi – ét:

    \left\{ \begin{matrix} x_{2} + x_{3} = - 2x_{1} \\ x_{2}.x_{3} = 3{x_{1}}^{2} - 2 \\ \end{matrix} ight.

    Ta có: \left\{ \begin{matrix} \Delta' = {x_{1}}^{2} - 3{x_{1}}^{2} + 2 > 0 \\ {x_{1}}^{2} + 2{x_{1}}^{2} + 3{x_{1}}^{2} - 2 eq 0 \\ {x_{1}}^{3} + (x_{2} + x_{3})^{3} - 3x_{2}x_{3}(x_{2} + x_{3}) = - 1 \\ \end{matrix} ight.\Leftrightarrow \left\{ \begin{matrix} - 1 < x_{1} < 1 \\ 3{x_{1}}^{2} - 1 eq 0 \\ {x_{1}}^{3} + ( - 2x_{1})^{3} - 3(3{x_{1}}^{2} - 2).( - 2x_{1}) = - 1 \\ \end{matrix} ight.

     

    \Leftrightarrow x_{1} = \frac{- 11 + \sqrt{165}}{22}.

    Vậy có đúng 1 đường thẳng thỏa mãn yêu cầu bài toán.

  • Câu 3: Vận dụng
    Xác định tính đúng sai của từng phương án

    Một công ty A có 120 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 3 000 000 đồng thì mỗi tháng mọi căn hộ đều có người thuê và cứ tăng thêm giá cho thuê mỗi căn hộ 100 nghìn đồng một tháng thì sẽ có 3 căn hộ bị bỏ trống. Gọi x (trăm nghìn) là số tiền tăng thêm.

    a) Số căn hộ còn lại sau khi tăng giá là 120 - 3x. Đúng||Sai

    b) Giá một căn hộ sau khi tăng là 30 - x (trăm nghìn). Sai||Đúng

    c) Tổng số tiền công ty thu được là S(x) = - 3x^{2} + 30x + 3600 (trăm nghìn). Đúng||Sai

    d) Công ty thu được nhiều tiền nhất khi giá thuê mỗi căn hộ là 4 (triệu đồng).Sai||Đúng

    Đáp án là:

    Một công ty A có 120 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 3 000 000 đồng thì mỗi tháng mọi căn hộ đều có người thuê và cứ tăng thêm giá cho thuê mỗi căn hộ 100 nghìn đồng một tháng thì sẽ có 3 căn hộ bị bỏ trống. Gọi x (trăm nghìn) là số tiền tăng thêm.

    a) Số căn hộ còn lại sau khi tăng giá là 120 - 3x. Đúng||Sai

    b) Giá một căn hộ sau khi tăng là 30 - x (trăm nghìn). Sai||Đúng

    c) Tổng số tiền công ty thu được là S(x) = - 3x^{2} + 30x + 3600 (trăm nghìn). Đúng||Sai

    d) Công ty thu được nhiều tiền nhất khi giá thuê mỗi căn hộ là 4 (triệu đồng).Sai||Đúng

    a) Đúng. Số căn hộ bị bỏ trống là 3x. Suy ra Số căn hộ còn lại sau khi tăng giá là 120 - 3x.

    b) Sai. Giá một căn hộ sau khi tăng là 30 + x (trăm ngìn).

    c) Đúng. Tổng số tiền công ty thu được là

    S(x) = (120 - 3x)(30 + x) = - 3x^{2} + 30x + 3600.

    d) Sai. Ta có S'(x) = - 6x + 30.

    Phương trình S'(x) = 0 \Leftrightarrow - 6x + 30 = 0 \Leftrightarrow x = 5.

    Bảng biến thiên

    Từ bảng biến thiên suy ra, công ty sẽ thu được nhiều tiền nhất khi giá căn hộ là 3,5 (triệu đồng).

  • Câu 4: Vận dụng
    Tính giá trị biểu thức

    Một đường thẳng cắt đồ thị hàm số y = x^{4} - 2x^{2} tại 4 điểm phân biệt có hoành độ là 0,1,m,n. Tính S = m^{2} + n^{2}.

    Hướng dẫn:

    Gọi phương trình đường thẳng là d:y = ax + b.

    Theo đề ta có 0,1,m,n là các nghiệm của phương trình: x^{4} - 2x^{2} - ax - b = 0 (1).

    Vì x=0 ,x=1 là nghiệm của phương trình (1) nên ta có: \left\{ \begin{matrix} b = 0 \\ a + b = - 1 \\ \end{matrix} ight.

    Khi đó phương trình (1) trở thành: x^{4} - 2x^{2} + x = 0 \Leftrightarrow x(x - 1)(x^{2} + x - 1) = 0.

    Dễ thấy m,n là nghiệm của phương trình: x^{2} + x - 1 = 0.

    S = m^{2} + n^{2} = (m + n)^{2} - 2mn = ( - 1)^{2} + 2 = 3.

  • Câu 5: Vận dụng
    Chọn đáp án đúng

    Tính tổng tất cả các giá trị của m biết đồ thị hàm số y = x^{3} + 2mx^{2} + (m + 3)x + 4 và đường thẳng y = x + 4 cắt nhau tại ba điểm phân biệt A(0\ ;\ 4), B, C sao cho diện tích tam giác IBC bằng 8\sqrt{2} với I(1\ ;\ 3).

    Hướng dẫn:

    +) Gọi đồ thị hàm số y = x^{3} + 2mx^{2} + (m + 3)x + 4 là \left( C_{m} ight) và đồ thị hàm số y = x + 4là (d).

    +) Phương trình hoành độ giao điểm của \left( C_{m} ight) và (d) là

    x^{3} + 2mx^{2} + (m + 3)x + 4 = x + 4

    \Leftrightarrow x^{3} + 2mx^{2} + (m + 2)x = 0\ (*)\Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x^{2} + 2mx + m + 2 = 0 \\ \end{matrix} ight.

    +) Gọi g(x) = x^{2} + 2mx + m + 2.

    +) (d) cắt \left( C_{m} ight) tại ba điểm phân biệt \Leftrightarrow phương trình (*) có ba nghiệm phân biệt

    \Leftrightarrow phương trình g(x) = 0 có hai nghiệm phân biệt khác 0

    \Leftrightarrow \left\{ \begin{matrix} {\Delta'}_{g} > 0 \\ g(0) eq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} m^{2} - m - 2 > 0 \\ m + 2 eq 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} \left\lbrack \begin{matrix} m < - 1 \\ m > 2 \\ \end{matrix} ight.\ \ \\ m eq - 2 \\ \end{matrix} ight.\ \ \ \ (a)

    +)x = 0 là hoành độ điểm A, hoành độ điểm B, C là hai nghiệm x_{1}, x_{2} của phương trình g(x) = 0

    +) BC^{2} = \left( x_{2} - x_{1} ight)^{2} + \left\lbrack \left( x_{2} + 4 ight) - \left( x_{1} + 4 ight) ightbrack^{2}

    = 2\left( x_{2} - x_{1} ight)^{2} (do B, C thuộc đường thẳng (d)

    = 2\left\lbrack \left( x_{2} + x_{1} ight)^{2} - 4x_{1}x_{2} ightbrack = 8\left( m^{2} - m - 2 ight)

    +) Viết phương trình đường thẳng (d) dưới dạng x - y + 4 = 0, ta có

    d\left( I,(d) ight) = \frac{|1 - 3 + 4|}{\sqrt{2}} = \sqrt{2}.

    +) S_{IBC} = 8\sqrt{2} \Leftrightarrow \frac{1}{2}BC.d\left( I,(d) ight) = 8\sqrt{2}

    \Leftrightarrow \frac{1}{4}BC^{2}.\left\lbrack d\left( I,(d) ight) ightbrack^{2} = 128

    \Leftrightarrow \frac{1}{4}8\left( m^{2} - m - 2 ight).2 = 128

    \Leftrightarrow m^{2} - m - 34 = 0 \Leftrightarrow \left\lbrack \begin{matrix} m = \frac{1 + \sqrt{137}}{2} \\ m = \frac{1 - \sqrt{137}}{2} \\ \end{matrix} ight. (thỏa điều kiện (a))

    +) Vậy tổng tất cả các giá trị m là 1.

  • Câu 6: Vận dụng
    Tìm các số thực dương m theo yêu cầu bài toán

    Cho hàm số y = x^{4} - 3x^{2} - 2. Tìm số thực dương m để đường thẳng y = m cắt đồ thị hàm số tại 2 điểm phân biệt A, B sao cho tam giác OAB vuông tại O, trong đó O là gốc tọa độ.

    Hướng dẫn:

    Hoành độ giao điểm của hai đồ thị hàm số là nghiệm của phương trình:

    x^{4} - 3x^{2} - 2 = m \Leftrightarrow x^{4} - 3x^{2} - 2 - m = 0\ \ \ \ \ \ \ \ \ (1).

    Vì m > 0 \Leftrightarrow - 2 - m < 0 hay phương trình (1) luôn có hai nghiệm phân biệt thỏa mãn:

    x^{2} = \frac{3 + \sqrt{4m + 17}}{2} \Rightarrow x_{1} = \sqrt{\frac{3 + \sqrt{4m + 17}}{2}}và x_{2} = - \sqrt{\frac{3 + \sqrt{4m + 17}}{2}}.

    Khi đó: A\left( x_{1};m ight), B\left( x_{2};m ight).

    Ta có tam giác OAB vuông tại O, trong đó O là gốc tọa độ \Leftrightarrow \overrightarrow{OA}.\overrightarrow{OB} = 0 \Leftrightarrow x_{1}.x_{2} + m^{2} = 0.

    \Leftrightarrow \frac{3 + \sqrt{4m + 17}}{2} = m^{2}

    \Leftrightarrow \left\{ \begin{matrix} 2m^{2} - 3 \geq 0 \\ 4m^{4} - 12m^{2} - 4m - 8 = 0 \\ \end{matrix} ight.\ \overset{m > 0}{\leftrightarrow}m = 2.

    Vậy m = 2 là giá trị cần tìm.

  • Câu 7: Vận dụng
    Tìm m thỏa mãn yêu cầu bài toán

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Số nghiệm thuộc đoạn \left\lbrack 0;\frac{7}{2} ightbrack của phương trình f\left( \cos x ight) = 1 bằng:

    Hướng dẫn:

    Dựa vào bảng biến thiến ta suy ra f\left( \cos x ight) = 1 \Leftrightarrow \left\lbrack \begin{matrix} \cos x = a < - 1\ \ \ \ (1) \\ \cos x = b \in ( - 1;0)\ \ \ (2) \\ \cos x = c \in (0;1)\ \ (3) \\ \cos x = d > 1\ \ (4) \\ \end{matrix} ight.

    Các phương trình (1) và (4) vô nghiệm

    Ta có bảng sau:

    Phương trình \cos x = b \in ( - 1;0) có 4 nghiệm thuộc \left\lbrack 0;\frac{7}{2} ightbrack

    Phương trình \cos x = c \in (0;1) có 3 nghiệm thuộc \left\lbrack 0;\frac{7}{2} ightbrack

    Vậy phương trình đã cho có tất cả 7 nghiệm thuộc đoạn \left\lbrack 0;\frac{7}{2} ightbrack.

  • Câu 8: Vận dụng
    Tính giá trị biểu thức

    Cho hàm số y = \frac{3x + 2}{x + 2},(C) và đường thẳng d:y = ax + 2b - 4. Đường thẳng d cắt ( C ) tại A, B đối xứng nhau qua gốc tọa độ O, khi đó T = a + b bằng

    Hướng dẫn:

    Xét phương trình hoành độ: \frac{3x + 2}{x + 2} = ax + 2b - 4\ ;\ x eq - 2.

    \Leftrightarrow ax^{2} + (2a + 2b - 7)x - 10 = 0\ (*).

    Đường thẳng d cắt ( C) tại hai điểm phân biệt A, B khi phương trình (*) có hai nghiệm phân biệt\Leftrightarrow \left\{ \begin{matrix} a eq 0 \\ (2a + 2b - 7)^{2} - 4a(4b - 10) > 0 \\ 4 eq 0\ \\ \end{matrix} ight.\ \ (2*)

    Gọi A\left( x_{1};ax_{1} + 2b - 4 ight);\ B\left( x_{2};ax_{2} + 2b - 4 ight).

    Do A, B đối xứng nhau qua gốc O nên \left\{ \begin{matrix} x_{1} + x_{2} = 0 \\ 4b - 8 = 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} x_{1} + x_{2} = 0 \\ b = 2 \\ \end{matrix} ight.

    Theo Viét của phương trình (*) ta có x_{1} + x_{2} = \frac{7 - 2a - 2b}{a}.

    \Rightarrow \frac{7 - 2a - 2b}{a} = 0 \Leftrightarrow 7 - 2a - 2b = 0 \Rightarrow a = \frac{3}{2}.

    Thay \left\{ \begin{matrix} a = \frac{3}{2} \\ b = 2 \\ \end{matrix} ight. vào điều kiện (2*) tháy thỏa mãn.

    Vậy a + b = \frac{7}{2}.

  • Câu 9: Vận dụng
    Chọn khẳng định đúng

    Cho đồ thị hàm số (C):y = \frac{2x + 1}{x + 2}. Giả sử M(a;b) \in (C) có khoảng cách đến đường thẳng d:y = 3x + 6 nhỏ nhất. Chọn khẳng định đúng?

    Hướng dẫn:

    Ta có: M\left( a;\frac{2a + 1}{a + 2} ight);(a eq - 2)

    Khoảng cách từ M đến đường thẳng (d) bằng:

    d(M;d) = \dfrac{\left| 3a - \dfrac{2a +1}{a + 2} + 6 ight|}{\sqrt{3^{2} + 1}}= \frac{1}{\sqrt{10}}.\left| 3a+ 6 - \frac{2a + 1}{a + 2} ight|= \frac{1}{\sqrt{10}}.\left|\frac{3a^{2} + 10a + 11}{a + 2} ight|

    Xét hàm số f(a) = \frac{3a^{2} + 10a + 11}{a + 2};(a eq - 2)

    f'(a) = \frac{3\left( a^{2} + 4a + 3 ight)}{(a + 2)^{2}} = 0 \Leftrightarrow \left\lbrack \begin{matrix} a = - 1 \\ a = - 3 \\ \end{matrix} ight.

    Ta có bảng biến thiên

    Vậy giá trị nhỏ nhất của hàm số \left| f(a) ight| = 4 tại a = - 1

    Vậy \left\{ \begin{matrix} a = - 1 \\ b = - 1 \\ \end{matrix} ight.\ \Rightarrow a + b = - 2

  • Câu 10: Vận dụng cao
    Tính giá trị của biểu thức

    Cho hàm số y = x^{4} + 2mx^{2} + m (với mlà tham số thực). Tập tất cả các giá trị của tham số m để đồ thị hàm số đã cho cắt đường thẳng y = - 3 tại bốn điểm phân biệt, trong đó có một điểm có hoành độ lớn hơn 2 còn ba điểm kia có hoành độ nhỏ hơn 1, là khoảng (a;b) (với a,b\mathbb{\in Q}, a,b là phân số tối giản). Khi đó, 15ab nhận giá trị nào sau đây?

    Hướng dẫn:

    Xét phương trình hoành độ giao điểm x^{4} + 2mx^{2} + m = - 3.

    Đặt x^{2} = t, t \geq 0. Khi đó phương trình trở thành t^{2} + 2mt + m + 3 = 0 (1)

    và đặt f(t) = t^{2} + 2mt + m + 3.

    Để đồ thị hàm số cắt đường thẳng y = - 3 tại 4 điểm phân biệt thì phương trình (1) có hai nghiệm thỏa mãn 0 < t_{1} < t_{2} và khi đó hoành độ bốn giao điểm là - \sqrt{t_{2}} < - \sqrt{t_{1}} < \sqrt{t_{1}} < \sqrt{t_{2}}.

    Do đó, từ điều kiện của bài toán suy ra \left\{ \begin{matrix} \sqrt{t_{2}} > 2 \\ \sqrt{t_{1}} < 1 \\ \end{matrix} ight. hay 0 < t_{1} < 1 < 4 < t_{2}.

    Điều này xảy ra khi và chỉ khi \left\{ \begin{matrix} f(0) > 0 \\ f(1) < 0 \\ f(4) < 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix} m + 3 > 0 \\ 3m + 4 < 0 \\ 9m + 19 < 0 \\ \end{matrix} ight.\ \Leftrightarrow - 3 < m < - \frac{19}{9}.

    Vậy a = - 3, b = - \frac{19}{9} nên 15ab = 95.

  • Câu 11: Vận dụng cao
    Chọn kết luận đúng

    Đồ thị của hàm số y = x^{4} - 2(m + 1)x^{2} + 2m + 1 (với m là tham số) cắt trục hoành tại bốn điểm phân biệt có hoành độ lập thành một cấp số cộng. Kết luận nào sau đây đúng?

    Hướng dẫn:

    Phương trình hoành độ giao điểm y = x^{4} - 2(m + 1)x^{2} + 2m + 1 = 0\ \ (1)

    Đặt t = x^{2};t \geq 0. Phương trình trở thành t^{2} - 2(m + 1)t + 2m + 1 = 0\ \ \ (2)

    Phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm dương phân biệt, nghĩa là \Leftrightarrow \left\{ \begin{matrix} \Delta' > 0 \\ S > 0 \\ P > 0 \\ \end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix} (m + 1)^{2} - (2m + 1) > 0 \\ m + 1 > 0 \\ 2m + 1 > 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\{ \begin{matrix}m eq 0 \\m > - 1 \\m > - \dfrac{1}{2} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}m eq 0 \\m > - \dfrac{1}{2} \\\end{matrix} ight.

    Gọi x_{1};x_{2};x_{3};x_{4};\left( x_{1} < x_{2} < x_{3} < x_{4} ight) là nghiệm cỉa phương trình (1) và t_{1};t_{2};\left( t_{1} < t_{2} ight) là nghiệm của phương trình (2)

    Theo giả thiết ta có:

    x_{4} - x_{3} = x_{3} - x_{2} = x_{2} - x_{1}

    \Leftrightarrow x_{4} - x_{3} = x_{3} - x_{2}

    \Leftrightarrow \sqrt{t_{2}} - \sqrt{t_{1}} = \sqrt{t_{1}} + \sqrt{t_{1}} \Leftrightarrow t_{2} = 9t_{1} > 0

    Ta có hệ:

    \left\{ \begin{matrix}t_{1} + t_{2} = 2(m + 1) \\t_{1}.t_{2} = 2m + 1 \\t_{1} = 9t_{2} \\\end{matrix} ight.\ \Leftrightarrow \left\{ \begin{matrix}t_{1} = \dfrac{m}{5} + \dfrac{1}{5} \\t_{2} = \dfrac{9m}{5} + \dfrac{9}{5} \\t_{1}.t_{2} = 2m + 1 \\\end{matrix} ight.

    \Leftrightarrow \left( \dfrac{m}{5} +\dfrac{1}{5} ight)\left( \dfrac{9m}{5} + \dfrac{9}{5} ight) = 2m + 1\Leftrightarrow \left\lbrack \begin{matrix}m = 4 \\m = - \dfrac{4}{9} \\\end{matrix} ight.

    Vậy m \in (2;6)

  • Câu 12: Vận dụng
    Chọn đồ thị ứng với hàm số đã cho

    Hình vẽ nào dưới đây là đồ thị của hàm số y = - \left( {a - x} ight){\left( {b - x} ight)^2} biết a > b > 0

    Hướng dẫn:

    Xét hàm số y = f\left( x ight) = - \left( {a - x} ight){\left( {b - x} ight)^2} = \left( {x - a} ight){\left( {x - b} ight)^2} ta có:

    \left\{ {\begin{array}{*{20}{c}} {\mathop {\lim }\limits_{x \to + \infty } f\left( x ight) = + \infty } \\ {\mathop {\lim }\limits_{x \to - \infty } f\left( x ight) = - \infty } \end{array}} ight. => Đồ thị hàm số có dạng chữ N xuôi

    Đồ thị hàm số cắt trục Oy tại điểm có tung độ y\left( 0 ight) = - a{b^2} mà a > 0 => y\left( 0 ight) < 0

    Mặt khác f'\left( x ight) = {\left( {x - b} ight)^2} + 2\left( {x - a} ight)\left( {a - b} ight) = \left( {x - b} ight)\left( {3x - 2a - b} ight)

    => \left\{ {\begin{array}{*{20}{c}} {f\left( b ight) = 0} \\ {f'\left( b ight) = 0} \end{array}} ight.

    => Đồ thị hàm số y = f(x) tiếp xúc với Ox tại điểm M\left( {b;0} ight)

  • Câu 13: Vận dụng cao
    Chọn đáp án đúng

    Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên.

    Số nghiệm thực của phương trình \left| f\left( x^{4} - 2x^{2} \right) \right| = 2 là

    Hướng dẫn:

    Phương trình \left| f\left( x^{4} - 2x^{2} ight) ight| = 2 \Leftrightarrow \left\lbrack \begin{matrix} f\left( x^{4} - 2x^{2} ight) = 2 \\ f\left( x^{4} - 2x^{2} ight) = - 2 \\ \end{matrix}. ight.

    * Phương trình f\left( x^{4} - 2x^{2} ight) = 2

    \Leftrightarrow \left\lbrack \begin{matrix} x^{4} - 2x^{2} = b,( - 1 < b < 0) \\ \begin{matrix} x^{4} - 2x^{2} = c,(0 < c < 1) \\ x^{4} - 2x^{2} = d,(2 < d < 3) \\ \end{matrix} \\ \end{matrix} ight..

    * Phương trình f\left( x^{4} - 2x^{2} ight) = - 2 \Leftrightarrow x^{4} - 2x^{2} = a,( - 2 < a < - 1).

    Đồ thị hàm số y = x^{4} - 2x^{2} như hình vẽ sau:

    Dựa vào đồ thị trên ta có:

    - Phương trình x^{4} - 2x^{2} = a,( - 2 < a < - 1) không có nghiệm thực.

    - Phương trình x^{4} - 2x^{2} = b,( - 1 < b < 0) có 4 nghiệm thực phân biệt.

    - Phương trình x^{4} - 2x^{2} = c,(0 < c < 1) có 2 nghiệm thực phân biệt.

    - Phương trình x^{4} - 2x^{2} = d,(2 < d < 3) có 2 nghiệm thực phân biệt.

    Vậy phương trình \left| f\left( x^{4} - 2x^{2} ight) ight| = 2 có 8 nghiệm thực phân biệt.

    Nhận xét: Khi bài toán chứa dấu giá trị tuyệt đối ta đi phá dấu giá trị tuyệt đối bằng phép biến đổi tương đương \left| f(x) ight| = A \Leftrightarrow \left\lbrack \begin{matrix} f(x) = A \\ f(x) = - A \\ \end{matrix} ight. .

  • Câu 14: Vận dụng
    Xác định tính đúng sai của từng phương án

    Anh H dự định sử dụng hết 5,5m2 kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép nối không đáng kể).

    Gọi a và h lần lượt là kích thước chiều rộng và chiều cao (theo đơn vị mét).

    Xét tính đúng sai của các khẳng định sau:

    a) Tổng diện tích 5 mặt của bể là S = 2a^{2} + 6ah . Đúng||Sai

    b) Ta có h = \frac{5,5 + 2a^{2}}{6a} . Sai|| Đúng

    c) Thể tích của bể là V = \frac{5,5a}{3} + \frac{2a^{3}}{3} . Sai|| Đúng

    d) Bể cá có dung tích lớn nhất bằng \frac{11\sqrt{33}}{54} . Đúng||Sai

    Đáp án là:

    Anh H dự định sử dụng hết 5,5m2 kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép nối không đáng kể).

    Gọi a và h lần lượt là kích thước chiều rộng và chiều cao (theo đơn vị mét).

    Xét tính đúng sai của các khẳng định sau:

    a) Tổng diện tích 5 mặt của bể là S = 2a^{2} + 6ah . Đúng||Sai

    b) Ta có h = \frac{5,5 + 2a^{2}}{6a} . Sai|| Đúng

    c) Thể tích của bể là V = \frac{5,5a}{3} + \frac{2a^{3}}{3} . Sai|| Đúng

    d) Bể cá có dung tích lớn nhất bằng \frac{11\sqrt{33}}{54} . Đúng||Sai

    a) Đúng. Kích thước đáy của bể lần lượt là 2a, a; chiều cao bể là h (a, h > 0). Tổng diện tích 5 mặt của bể là:

    S = 2a^{2} + 2ah + 4ah = 2a^{2} + 6ah

    b) Sai. Theo đề bài ta có: 2a^{2} + 6ah = 5,5 \Rightarrow h = \frac{5,5 - 2a^{2}}{6a};\left( 0 < a < \frac{5\sqrt{5}}{2} ight).

    c) Sai. Gọi V là thể tích của bể cá, ta có:

    V = 2a^{2}h = \frac{2a^{2}\left( 5,5 - 2a^{2} ight)}{6a} = \frac{5,5a}{3} - \frac{2a^{3}}{3}

    d) Đúng. Ta có: V' = \frac{5,5}{3} - \frac{6a^{2}}{3}

    V' = 0 \Leftrightarrow \dfrac{5,5}{3}- \dfrac{6a^{2}}{3} = 0 \Leftrightarrow \left\lbrack \begin{matrix}a = \dfrac{\sqrt{33}}{6}(tm) \\a = - \dfrac{\sqrt{33}}{6}(ktm) \\\end{matrix} ight.

    Bảng biến thiên:

    Vậy dung tích lớn nhất của bể cá bằng \frac{11\sqrt{33}}{54}.

  • Câu 15: Vận dụng cao
    Tìm m để biểu thức đạt giá trị nhỏ nhất

    Cho hàm số y = \frac{x}{1 - x}\ \ \ \ \ (C) và điểm A( - 1;1). Tìm m để đường thẳng d:\ \ y = mx - m - 1 cắt (C)tại hai điểm phân biệt M,N sao cho AM^{2} + AN^{2} đạt giá trị nhỏ nhất.

    Hướng dẫn:

    Phương trình hoành độ giao điểm của (C) và d là: \frac{x}{1 - x} = mx - m - 1 (đk: x eq 1)

    \begin{matrix} \Rightarrow x = (1 - x)(mx - m - 1) \\ \Leftrightarrow x = mx - m - 1 - mx^{2} + mx + x \\ \Leftrightarrow mx^{2} - 2mx + m + 1 = 0\ \ (*) \\ \end{matrix}

    Để (C) và d cắt nhau tại hai điểm phân biệt M,N thì (*) phải có 2 nghiệm phân biệt khác 1 \Leftrightarrow \left\{ \begin{matrix} m eq 0 \\ \Delta' = m^{2} - m(m + 1) = - m > 0 \\ m - 2m + m + 1 eq 0 \\ \end{matrix} ight.

    \Leftrightarrow m < 0

    Giả sửM\left( x_{1};y_{1} ight),N\left( x_{2};y_{2} ight).

    Theo hệ thức viét : x_{1} + x_{2} = 2;\ \ x_{1}x_{2} = \frac{m + 1}{m}

    \Rightarrow y_{1} + y_{2} = m\left( x_{1} + x_{2} ight) - 2m - 2 = 2m - 2m - 2 = - 2

    và y_{1}.y_{2} = \left( mx_{1} - m - 1 ight)\left( mx_{2} - m - 1 ight)

    = m^{2}x_{1}x_{2} - m(m + 1)\left( x_{1} + x_{2} ight) + (m + 1)^{2}

    = m(m + 1) - 2m(m + 1) + (m + 1)^{2} = m+ 1

    Ta có:

    AM^{2} + AN^{2} = \left( x_{1} + 1 ight)^{2} + \left( y_{1} - 1 ight)^{2} + \left( x_{2} + 1 ight)^{2} + \left( y_{2} - 1 ight)^{2}

    = \left( x_{1} + x_{2} + 2 ight)^{2} - 2\left( x_{1} + 1 ight)\left( x_{2} + 1 ight) + \left( y_{1} + y_{2} - 2 ight)^{2} - 2\left( y_{1} - 1 ight)\left( y_{2} - 1 ight)

    = \left( x_{1} + x_{2} + 2 ight)^{2} - 2\left( x_{1}x_{2} + x_{1} + x_{2} + 1 ight)+ \left( y_{1} + y_{2} - 2 ight)^{2} - 2\left( y_{1}y_{2} - \left( y_{1} + y_{2} ight) + 1 ight)

    = (2 + 2)^{2} - 2\left( \frac{m + 1}{m} + 2 + 1 ight)+ ( - 2 - 2)^{2} - 2\left( m + 1 - ( - 2) + 1 ight)

    = 18 - 2\left( \frac{m + 1}{m} ight) - 2m = 18 - 2 - 2.\frac{1}{m} - 2m

    = 16 + 2.\left\lbrack \frac{1}{- m} + ( - m) ightbrack \geq 16 + 2.2 = 20 (Áp dụng BĐT Côsi)

    Suy ra: AM^{2} + AN^{2} đạt giá trị nhỏ nhất là 20 khi \frac{1}{- m} = - m \Leftrightarrow m^{2} = 1 \Leftrightarrow \left\lbrack \begin{matrix} m = 1 \\ m = - 1 \\ \end{matrix} ight.

    Vậy m = - 1 (vì m < 0).

  • Câu 16: Vận dụng
    Ghi đáp án vào ô trống

    Trong hệ trục toạ độ (Oxy), cho đồ thị hàm số (C):y = \frac{x^{2} + x + 1}{x + 1} với x > - 1 mô tả chuyển động của một chiếc thuyền trên biển. Một trạm phát sóng đặt tại điểm I( - 1; - 1), biết hoành độ điểm M thuộc đồ thị (C) mà tại đó thuyền thu được sóng tốt nhất là x_{0} = \frac{1}{\sqrt[n]{a}} - b (loại trừ các điều kiện ảnh hưởng đến việc thu phát sóng). Tính giá trị biểu thức P = a.n + b ?

    Chỗ nhập nội dung câu trả lời tự luận
    Đáp án là:

    Trong hệ trục toạ độ (Oxy), cho đồ thị hàm số (C):y = \frac{x^{2} + x + 1}{x + 1} với x > - 1 mô tả chuyển động của một chiếc thuyền trên biển. Một trạm phát sóng đặt tại điểm I( - 1; - 1), biết hoành độ điểm M thuộc đồ thị (C) mà tại đó thuyền thu được sóng tốt nhất là x_{0} = \frac{1}{\sqrt[n]{a}} - b (loại trừ các điều kiện ảnh hưởng đến việc thu phát sóng). Tính giá trị biểu thức P = a.n + b ?

    Chỗ nhập nội dung câu trả lời tự luận
  • Câu 17: Vận dụng cao
    Bất phương trình chưa tham số m nghiệm đúng khi

    Cho hàm số f\left( x ight) có đạo hàm y = f'\left( x ight) liên tục trên \mathbb{R} và có bảng biến thiên như sau:

    Bất phương trình chưa tham số m nghiệm đúng khi

    Bất phương trình f\left( x ight) > - {x^3} + {x^2} - x + m (m là tham số thực) nghiệm đúng với \forall x \in \left( { - 1;1} ight) khi và chỉ khi

    Hướng dẫn:

    Ta có: f\left( x ight) > - {x^3} + {x^2} - x + m \Rightarrow m < f\left( x ight) + {x^3} - {x^2} + x\left( * ight)

    Xét hàm số g\left( x ight) = f\left( x ight) + {x^3} - {x^2} + x với \forall x \in \left( { - 1;1} ight)

    Ta có: g'\left( x ight) = f'\left( x ight) + 3{x^2} - 2x + 1 > 0;\forall x \in \left( { - 1;1} ight)

    => Hàm số g(x) luôn đồng biến trên \left( { - 1;1} ight)

    Ta có bảng biến thiên như sau:

    Bất phương trình chưa tham số m nghiệm đúng khi

    => (*) nghiệm đúng \forall x \in \left( { - 1;1} ight) khi m \leqslant g\left( { - 1} ight) = f\left( { - 1} ight) - 3

  • Câu 18: Vận dụng
    Chọn mệnh đề đúng

    Đường thẳng y = m^{2} cắt đồ thị hàm số y = x^{4} - x^{2} - 10 tại hai điểm phân biệt sao cho tam giác OAB vuông (với O là gốc tọa độ). Mệnh đề nào sau đây đúng?

    Hướng dẫn:

    Xét hàm số y = x^{4} - x^{2} - 10 ta có y' = 4x^{3} - 2x = 0\Leftrightarrow \left\lbrack \begin{matrix}x = 0 \\x = \dfrac{\sqrt{2}}{2} \\x = - \dfrac{\sqrt{2}}{2} \\\end{matrix} ight.

    Ta có bảng biến thiên như sau:

    Vì m^{2} \geq 0;\forall m nên từ bảng biến thiên ta thấy đường thẳng y = m^{2} luôn cắt đồ thị hàm số y = x^{4} - x^{2} - 10 tại những cặp điểm đối xứng nhau qua trục tung.

    Giả sử A\left( x_{1};m^{2} ight);B\left( - x_{1};m^{2} ight). Tam giác OAB vuông

    \Leftrightarrow \overrightarrow{OA}.\overrightarrow{OB} = \overrightarrow{0} \Leftrightarrow - {x_{1}}^{2} + m^{4} = 0 \Leftrightarrow x_{1} = m^{2}

    Suy ra A\left( m^{2};m^{2} ight) vì A\left( m^{2};m^{2} ight) thuộc đồ thị hàm số nên

    m^{8} - m^{4} - 10 = m^{2} \Leftrightarrow m^{2} = 2 \in (1;3)

  • Câu 19: Vận dụng cao
    Xác định số nghiệm thực của phương trình

    Cho hàm số f(x) có đồ thị là đường cong như hình vẽ bên dưới.

    Số nghiệm thực phân biệt của phương trình f\left( x^{3}f(x) \right) + 1 = 0 là

    Hướng dẫn:

    Dựa vào đồ thị, ta thấy f\left( x^{3}f(x) ight) + 1 = 0

    \Leftrightarrow f\left( x^{3}f(x) ight) = - 1

    \Leftrightarrow \left\lbrack \begin{matrix} x^{3}f(x) = a \in ( - 6; - 5)(1) \\ x^{3}f(x) = b \in ( - 3; - 2)(2) \\ x^{3}f(x) = 0(3) \\ \end{matrix} ight.

    + Phương trình (3) tương đương \left\lbrack \begin{matrix} x = 0 \\ f(x) = 0 \\ \end{matrix} ight.

    \Leftrightarrow \left\lbrack \begin{matrix} x = 0 \\ x = x_{1},\left( - 6 < x_{1} < a < - 5 ight) \\ \end{matrix} ight.

    + Các hàm số g(x) = \frac{a}{x^{3}} và h(x) = \frac{b}{x^{3}} đồng biến trên các khoảng ( - \infty;0) và (0; + \infty), và nhận xét rằng x = 0 không phải là nghiệm của phương trình (1) nên: (1) \Leftrightarrow \left\lbrack \begin{matrix} f(x) = g(x) \\ f(x) = h(x) \\ \end{matrix} ight..

    + Trên khoảng ( - \infty;0), ta có \left\{ \begin{matrix} \lim_{x ightarrow - \infty}f(x) = + \infty;\lim_{x ightarrow 0^{-}}f(x) = - 1 \\ \lim_{x ightarrow - \infty}g(x) = \lim_{x ightarrow - \infty}h(x) = 0 \\ \lim_{x ightarrow 0^{-}}g(x) = \lim_{x ightarrow 0^{-}}h(x) = + \infty \\ \end{matrix} ight.

    nên các phương trình f(x) = g(x) và f(x) = h(x) có nghiệm duy nhất.

    + Trên khoảng (0; + \infty), ta có \left\{ \begin{matrix} \lim_{x ightarrow + \infty}f(x) = - \infty;\lim_{x ightarrow 0^{+}}f(x) = - 1 \\ \lim_{x ightarrow + \infty}g(x) = \lim_{x ightarrow + \infty}h(x) = 0 \\ \lim_{x ightarrow 0^{+}}g(x) = \lim_{x ightarrow 0^{+}}h(x) = - \infty \\ \end{matrix} ight.

    nên các phương trình f(x) = g(x) và f(x) = h(x) có nghiệm duy nhất.

    Do đó, phương trình f\left( x^{3}f(x) ight) + 1 = 0 có 6 nghiệm phân biệt.

  • Câu 20: Vận dụng
    Chọn đáp án đúng:

    Đường thẳng d: y = x + 4 cắt đồ thị hàm số y = x^{3} + 2mx^{2} + (m + 3) x+ 4 tại ba điểm phân biệt A(0;4), B, C sao cho tam giác MBC có diện tích bằng 4, với M(1;3). Các giá trị của m nhận được là:

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (60%):
    2/3
  • Thông hiểu (40%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Tải file làm trên giấy
1
42 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này