Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Đường cong có dạng của đồ thị hàm số bậc với hệ số
nên chỉ có hàm số
thỏa yêu cầu bài toán.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
Đường cong có dạng của đồ thị hàm số bậc với hệ số
nên chỉ có hàm số
thỏa yêu cầu bài toán.
Cho hình vẽ:
Hàm số nào sau đây có đồ thị như hình vẽ bên?
Nhận thấy dạng đồ thị của hàm số bậc ba
Mặt khác đồ thị cắt trục tung tại điểm có tung độ âm nên hàm số tương ứng với đồ thị là .
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án dưới đây. Hỏi hàm số đó là hàm số nào?
Từ đồ thị : và đây là đồ thị hàm bậc ba nên ta chọn phương án
Đồ thị hàm số và đồ thị hàm số
có bao nhiêu điểm chung?
Phương trình hoành độ giao điểm:
.
Do phương trình có nghiệm nên đồ thị hai hàm số có
điểm chung.
Điểm nào sau đây thuộc đồ thị hàm số ?
Thay vào
ta được:
Vậy thuộc đồ thị hàm số
.
Cho hàm số , hàm số
liên tục trên
và có đồ thị như hình vẽ bên. Bất phương trình
(m là tham số thực) nghiệm đúng với mọi
khi và chỉ khi
Minh họa đồ thị như hình vẽ dưới đây:
Ta có:
.
Gọi
Theo đồ thị ta thấy .
Vậy hàm số liên tục và nghịch biến trên
Do đó
.
Số điểm giao điểm của đồ thị hàm số và trục hoành là:
Xét phương trình:
Số điểm giao điểm của đồ thị hàm số và trục hoành là 2.
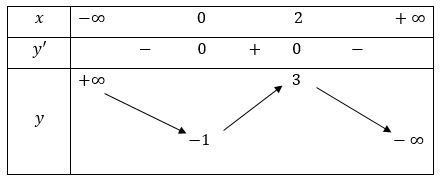
Cho hàm số có đồ thị như hình vẽ:
Tập hợp các giá trị của tham số để phương trình
có đúng ba nghiệm phân biệt là:
Đồ thị hàm số có được bằng cách tịnh tiến đồ thị hàm số
sang trái hoặc sang phải theo phương song song với trục hoành
đơn vị.
Suy ra phương trình có đúng ba nghiệm phân biệt khi và chỉ khi
.
Đồ thị hàm số nào có dạng đường trong như trong hình vẽ dưới đây?
Dựa vào hình dáng đồ thị suy ra đồ thị hàm số bậc 4 trùng phương có hệ số nên hàm số cần tìm là
.
Cho hàm số với
là tham số thực. Xét tính đúng sai của các khẳng định sau:
a) Tập xác định . Đúng||Sai
b) . Sai|| Đúng
c) Hàm số đồng biến trên (−∞; 0) khi và chỉ khi m < 1. Sai|| Đúng
d) Hàm số đồng biến trên (−∞; 0) khi và chỉ khi 0 ≤ m < 1. Đúng||Sai
Cho hàm số với
là tham số thực. Xét tính đúng sai của các khẳng định sau:
a) Tập xác định . Đúng||Sai
b) . Sai|| Đúng
c) Hàm số đồng biến trên (−∞; 0) khi và chỉ khi m < 1. Sai|| Đúng
d) Hàm số đồng biến trên (−∞; 0) khi và chỉ khi 0 ≤ m < 1. Đúng||Sai
a) Tập xác định .
b)
c) Sai.
Hàm số đã cho đồng biến trên (−∞; 0) khi và chỉ khi
.
d) Đúng
Cho hàm số có đồ thị
Tìm số giao điểm của
và trục hoành.
Pthd của và trục hoành là:
có
giao điểm.
Chú ý: Ở bài toán này hoàn toàn có thể giải trực tiếp bằng Casio với phương trình , nhưng chắc chắn thao tác bấm máy sẽ chậm hơn việc tính tay (thậm chí bài này không cần nháp khi mà kết quả đã hiện ra luôn khi ta đọc đề xong). Vì vậy, Casio là điều không cần thiết với câu hỏi này.
Cho hàm số có đồ thị là đường cong trong hình bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là
Từ đồ thị ta thấy đồ thị hàm số cắt trục tung tại điểm có tọa độ .
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình bên?
Đường cong trong hình là đồ thị hàm trùng phương có hệ số .
Số giao điểm của đồ thị hàm số và đồ thị hàm số
là
Số giao điểm của đồ thị hàm số và đồ thị hàm số
chính là số nghiệm thực của phương trình
.
Đồ thị hàm số có bao nhiêu điểm có tọa độ nguyên?
Ta có:
Với đồ thị hàm số đã cho có đúng 1 điểm có tọa độ nguyên.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình sau:
Đồ thị của hàm số thỏa mãn bài toán.
Cho hàm số có đồ thị như hình vẽ.
Số nghiệm thực của phương trình là:
Ta có: .
Do đường thẳng cắt đồ thị hàm số
tại 3 điểm phân biệt nên suy ra phương trình đã cho có 3 nghiệm.
Đồ thị hàm số nào dưới đây có dạng như đường cong hình bên
Qua đồ thị là hàm bậc 3 nên loại ,
Bên phải ngoài cùng của đồ thị đi xuống nên hệ số a < 0
Loại đáp án
Gọi là số giao điểm của hai đồ thị
và
. Tìm
.
Xét phương trình hoành độ giao điểm của hai đồ thị và
:
Với .
Với .
Nên hai đồ thị trên có hai giao điểm là và
.
Vậy .
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

