Trong không gian với hệ toạ độ , cho ba điểm
. Phương trình mặt phẳng
đi qua
và cách
một khoảng lớn nhất?
Hình vẽ minh họa
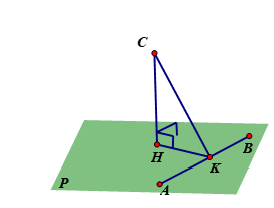
Gọi lần lượt là hình chiếu
của lên mp
và doạn thẳng
Ta có : lớn nhất khi
. Khi đó mặt phẳng
đi qua
và vuông với mặt phẳng
Ta có

