Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập trắc nghiệm Toán 12 Cánh Diều Bài 2 (Mức độ Dễ)

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 20 câu
  • Điểm số bài kiểm tra: 20 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Nhận biết
    Chọn mệnh đề đúng

    Xét hàm số f(x) = - \frac{4}{3}x^{3} - 2x^{2} - x - 3 trên \lbrack - 1;1brack. Mệnh đề nào sau đây là đúng?

    Hướng dẫn:

    Đạo hàm f'(x) = - 4x^{2} - 4x - 1 = -(2x + 1)^2 \leq 0,\ \forall x\mathbb{\in R}.

    Suy ra hàm số f(x) nghịch biến trên đoạn \lbrack - 1;1brack nên có giá trị nhỏ nhất tại x = 1 và giá trị lớn nhất tại x = - 1.

  • Câu 2: Nhận biết
    Tính giá trị biểu thức

    Cho hàm số y = \frac{2x + 3}{x - 2}. Giả sử M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \lbrack 0;1brack. Khi đó giá trị của biểu thức S = M + m là:

    Hướng dẫn:

    Ta có: y' = \frac{- 7}{(x - 2)^{2}} < 0;\forall x \in \lbrack 0;1brack

    Vậy \left\{ \begin{matrix}M = y(0) = - \dfrac{3}{2} \\m = y(1) = - 5 \\\end{matrix} ight.\ \Rightarrow S = M + m = -\dfrac{13}{2}

  • Câu 3: Nhận biết
    Chọn khẳng định đúng

    Cho hàm số có bảng biến thiên như hình dưới đây.

    Chọn khẳng định đúng

    Khẳng định nào sau đây là đúng?

    Hướng dẫn:

    Từ bảng biến thiên ta nhận thấy đạo hàm của hàm số đổi dấu từ dương sang âm qua nghiệm 0 nên hàm số đạt cực đại tại 0 và giá trị cực đại của hàm số bằng 0.

  • Câu 4: Nhận biết
    GTLN của hàm số trên khoảng là bao nhiêu?

    Cho hàm số y = f(x) và có bảng biến thiên trên [-2; 3) như sau:

    GTLN của hàm số trên khoảng là bao nhiêu?

    Giá trị lớn nhất của hàm số trên đoạn [-2; 3] bằng:

    Hướng dẫn:

    Từ đồ thị của hàm số y = f(x) ta thấy hàm số y = f(x) xác định và liên tục trên đoạn [-2; 3]

    Ta có: f(x) ∈ [-2; 3] với \forall x \in \mathbb{R} => \mathop {\max }\limits_{\left[ { - 2;3} ight]} f\left( x ight) = f\left( 3 ight) = 4

  • Câu 5: Thông hiểu
    Tìm giá trị lớn nhất của hàm số

    Tìm giá trị lớn nhất M của hàm số f(x) = x - \frac{1}{x} trên (0;3brack.

    Hướng dẫn:

    Đạo hàm f'(x) = 1 + \frac{1}{x^{2}} > 0,\ \forall x \in (0;3).

    Suy ra hàm số f(x) đồng biến trên (0;3brack nên đạt giá trị lớn nhất tại x = 3 và \max_{(0;3brack}f(x) = f(3) = \frac{8}{3}.

  • Câu 6: Nhận biết
    Xác định giá trị nhỏ nhất của hàm số

    Hàm số y = f(x) = x^{3} - 7x^{2} + 11x - 2 trên đoạn \lbrack 0;2brack có giá trị nhỏ nhất bằng:

    Hướng dẫn:

    Ta có: y' = 3x^{2} - 14x + 11

    \Rightarrow y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = \frac{11}{3} \\ \end{matrix} ight.. Khi đó f(0) = - 2;f(1) = 3;f(2) = 0 suy ra \min_{\lbrack 0;2brack}f(x) = - 2.

  • Câu 7: Nhận biết
    Cho hàm số y = f(x) có đồ thị sau:

    Toán 12 bài 2

    Giá trị lớn nhất của hàm số trên đoạn [0;1] là:

  • Câu 8: Thông hiểu
    Tìm giá trị của M - n

    Cho hàm số y = f(x) liên tục trên đoạn \lbrack - 2\ ;\ 6brack và có đồ thị như hình vẽ bên dưới.

    Gọi Mvà mlần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \lbrack - 2\ ;\ 6brack. Giá trị của M - m bằng

    Hướng dẫn:

    Từ đồ thị suy ra - 4 \leq f(x) \leq 5 \forall x \in \lbrack - 2;6brack;f(1) = - 4;f(4) = 5

    \Rightarrow \left\{ \begin{matrix} M = 5 \\ m = - 4 \\ \end{matrix} ight. \Rightarrow M - m = 9.

  • Câu 9: Thông hiểu
    Chọn phương án đúng

    Giá trị nhỏ nhất của hàm số y = x + \frac{2}{x} - \left( 1 + \sqrt{2} \right)^{2} trên khoảng (0; + \infty)

    Hướng dẫn:

    Hàm số xác định và liên tục trên khoảng (0; + \infty).

    y' = 1 - \frac{2}{x^{2}} = \frac{x^{2} - 2}{x^{2}}.

    y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = \sqrt{2} \\ x = - \sqrt{2} \\ \end{matrix} ight.\ .

    Bảng biến thiên:

    Vậy \min_{(0; + \infty)}y = f\left( \sqrt{2} ight) = - 3.

  • Câu 10: Nhận biết
    Khẳng định nào sau đây đúng?
  • Câu 11: Nhận biết
    Chọn mệnh đề đúng

    Cho hàm số y = f(x) có bảng biến thiên trên đoạn \lbrack - 5;7brack như sau:

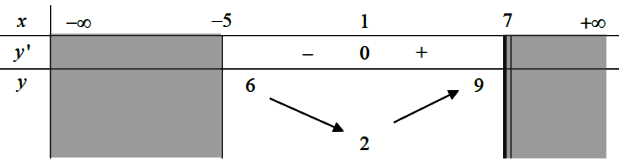
    Mệnh đề nào sau đây đúng?

    Hướng dẫn:

    Từ bảng biến thiên ta suy ra \min_{\lbrack - 5;7brack}y = 2

  • Câu 12: Nhận biết
    Tìm giá trị lớn nhất của hàm số

    Tìm giá trị lớn nhất của hàm số f(x) = 2x^{3} + 3x^{2} - 12x + 2 trên đoạn [ - 1;2]?

    Hướng dẫn:

    Đạo hàm f'(x) = 6x^2 + 6x -12

    \Rightarrow f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \in \lbrack - 1;2brack \\ x = - 2 otin \lbrack - 1;2brack \\ \end{matrix} ight.

    Ta có \left\{ \begin{matrix} f( - 1) = 15 \\ f(1) = - 5 \\ f(2) = 6 \\ \end{matrix} ight.\ \Rightarrow \max_{\lbrack - 1;2brack}f(x) = 15 .

  • Câu 13: Nhận biết
    Xét tính đúng sai của các nhận định

    Cho hàm số y = f(x) xác định và liên tục trên \mathbb{R}, có đồ thị như hình vẽ bên:

    Xét tính đúng sai của các nhận định dưới đây?

    a) Giá trị lớn nhất của hàm số trên đoạn \lbrack - 2;2\rbrack là - 1. Đúng||Sai

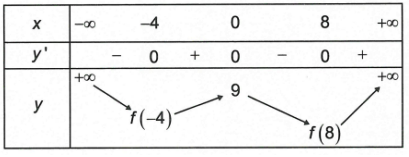
    b) Giá trị nhỏ nhất của hàm số trên \lbrack 0; + \infty) là - 5. Đúng||Sai

    c) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên ( - \infty;1\rbrack là 2. Sai||Đúng

    d) Hàm số đạt giá trị nhỏ nhất trên đoạn \lbrack - 1;2\rbrack tại điểm x = 1. Đúng||Sai

    Đáp án là:

    Cho hàm số y = f(x) xác định và liên tục trên \mathbb{R}, có đồ thị như hình vẽ bên:

    Xét tính đúng sai của các nhận định dưới đây?

    a) Giá trị lớn nhất của hàm số trên đoạn \lbrack - 2;2\rbrack là - 1. Đúng||Sai

    b) Giá trị nhỏ nhất của hàm số trên \lbrack 0; + \infty) là - 5. Đúng||Sai

    c) Hiệu giữa giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên ( - \infty;1\rbrack là 2. Sai||Đúng

    d) Hàm số đạt giá trị nhỏ nhất trên đoạn \lbrack - 1;2\rbrack tại điểm x = 1. Đúng||Sai

    a. Đúng

    b. Đúng

    c. Sai

    d. Đúng

  • Câu 14: Nhận biết
    Tìm giá trị lớn nhất của hàm số

    Tìm giá trị lớn nhất của hàm số y = f(x) = x4 – 2x2 + 1 trên đoạn [0; 2].

    Hướng dẫn:

    Xét hàm số f(x) = x4 – 2x2 + 1 trên [0; 2] có:

    f’(x) = 4x3 – 4x

    f’(x) = 0 => \left\{ {\begin{array}{*{20}{c}}{x \in \left[ {0;2} ight]} \\ {4{x^3} - 4x = 0} \end{array}} ight. \Leftrightarrow \left[ {\begin{array}{*{20}{c}} {x = 0} \\ {x = 1} \end{array}} ight.

    Tính f(0) = 1; f(1) = 0; f(2) = 9

    Vậy \mathop {\max }\limits_{\left[ {0;2} ight]} f\left( x ight) = f\left( 2 ight) = 9

  • Câu 15: Nhận biết
    Tìm điều kiện của tham số m

    Cho hàm số y = f(x) liên tục trên \lbrack 2;5brack và có đồ thị như hình vẽ:

    Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \lbrack 2;5brack lần lượt là M;m. Kết luận nào sau đây đúng?

    Hướng dẫn:

    Quan sát đồ thị ta thấy \left\{ \begin{matrix} \max_{\lbrack 2;5brack}y = M = 4 \\ \min_{\lbrack 2;5brack}y = m = - 6 \\ \end{matrix} ight.\ \Rightarrow M - m = 10

  • Câu 16: Nhận biết
    Xác định giá trị nhỏ nhất

    Cho hàm số y = f(x) có bảng biến thiên như sau:

    Giá trị nhỏ nhất của hàm số đã cho trên đoạn \lbrack - 2;3brack bằng bao nhiêu?

    Hướng dẫn:

    Giá trị nhỏ nhất của hàm số đã cho trên đoạn \lbrack - 2;3brack bằng - 3.

  • Câu 17: Thông hiểu
    Chọn đáp án đúng

    Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x^{3} - 3x^{2} + (4 - m)x đồng biến trên khoảng (2; + \infty) là:

    Hướng dẫn:

    Tập xác định D\mathbb{= R}

    Ta có: y' = 3x^{2} - 6x + 4 - m

    Hàm số đồng biến trên khoảng (2; + \infty) \Leftrightarrow y' \geq 0;\forall x \in (2; + \infty)

    \Leftrightarrow m \leq 3x^{2} - 6x + 4;\forall x \in (2; + \infty)

    Xét hàm số g(x) = 3x^{2} - 6x + 4 trên khoảng (2; + \infty).

    Ta có: g'(x) = 6x - 6;g'(x) = 0 \Leftrightarrow x = 1

    Ta có bảng biến thiên

    Dựa vào bảng biến thiên ta có: m \leq g(x);;\forall x \in (2; + \infty) \Leftrightarrow m \leq 4

    Vậy m \leq 4 thỏa mãn yêu cầu bài toán.

  • Câu 18: Nhận biết
    Xác định tính đúng sai của từng phương án

    Cho hàm số y = f(x) xác định trên tập D và một số thực M. Xét tính đúng sai của các khẳng định sau:

    a) Nếu f(x) \leq M,\forall x \in D thì \underset{D}{\max f(x)} = M. Sai|| Đúng

    b) Nếu f(x) \geq M,\forall x \in D thì \underset{D}{\min f(x)} = M. Sai|| Đúng

    c) Nếu f(x) = M,\forall x \in D thì \underset{D}{\max f(x)} = M. Đúng||Sai

    d) Nếu f(x) = M,\forall x \in D thì \underset{D}{\min f(x)} = M. Đúng||Sai

    Đáp án là:

    Cho hàm số y = f(x) xác định trên tập D và một số thực M. Xét tính đúng sai của các khẳng định sau:

    a) Nếu f(x) \leq M,\forall x \in D thì \underset{D}{\max f(x)} = M. Sai|| Đúng

    b) Nếu f(x) \geq M,\forall x \in D thì \underset{D}{\min f(x)} = M. Sai|| Đúng

    c) Nếu f(x) = M,\forall x \in D thì \underset{D}{\max f(x)} = M. Đúng||Sai

    d) Nếu f(x) = M,\forall x \in D thì \underset{D}{\min f(x)} = M. Đúng||Sai

    a) Khẳng định này sai, cần bổ sung thêm điều kiện \exists x_{0} \in D để f\left( x_{0} ight) = M.

    b) Khẳng định này sai, cần bổ sung thêm điều kiện \exists x_{0} \in D để f\left( x_{0} ight) = M.

    c) Nếu f(x) = M,\forall x \in D thì f(x) là hàm hằng trên D (đồ thị là đường thẳng nằm ngang).

    Suy ra \underset{D}{\max f(x)} = M.

    d) Nếu f(x) = M,\forall x \in D thì f(x) là hàm hằng trên D (đồ thị là đường thẳng nằm ngang).

    Suy ra\underset{D}{\min f(x)} = M.

  • Câu 19: Thông hiểu
    Chọn đáp án đúng

    Một chất điểm chuyển động với vận tốc được cho bởi công thức v(t) = - t^{2} + 4t + 2 với t (giây) là khoảng thời gian tính từ khi chất điểm bắt đầu chuyển động. Hỏi tại thời điểm nào thì vận tốc của chất điểm là lớn nhất?

    Hướng dẫn:

    Ta có: v(t) = - t^{2} + 4t + 2 với t > 0.

    v'(t) = - 2t + 4

    v'(t) = 0 \Leftrightarrow - 2t + 4 = 0 \Leftrightarrow t = 2 (thỏa mãn).

    Bảng biến thiên

    Dựa vào bảng biến thiên, tại thời điểm t = 2 giây thì vận tốc của chất điểm là lớn nhất.

  • Câu 20: Nhận biết
    Tính giá trị biểu thức P

    Biết rằng hàm số f(x) = x^{3} - 3x^{2} - 9x + 28 đạt giá trị nhỏ nhất trên \lbrack 0;4brack tại điểm x_{0}. Khi đó giá trị biểu thức P = x_{0} + 2021 bằng:

    Hướng dẫn:

    Ta có: y' = 3x^{2} - 6x - 9

    y' = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 1 \\ x = 3 \\ \end{matrix} ight.

    Mà \left\{ \begin{matrix} f(0) = 28 \\ f(3) = 1 \\ f(4) = 8 \\ \end{matrix} ight.\ \Rightarrow \min_{\lbrack 0;4brack}f(x) = 1 khi x = 3

    Suy ra x_{0} = 3 \Rightarrow P = x_{0} + 2021 = 2024.

0/20
20 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (75%):
    2/3
  • Thông hiểu (25%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
1
12 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Lớp 12
Xem thêm