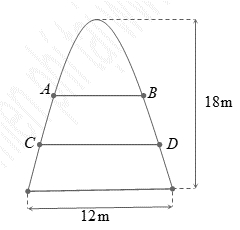
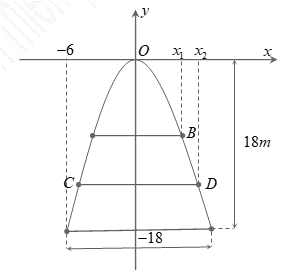
Cho là hình phẳng giới hạn bởi parabol
và nửa elip có phương trình
(với
) và trục hoành (phần tô đậm trong hình vẽ).
Gọi là diện tích của, biết
(với
). Tính
?
Hoành độ giao điểm của hai đồ thị:
Do tính chất đối xứng của đồ thị nên
. Đặt
Đổi cận
Với
Suy ra
Vậy