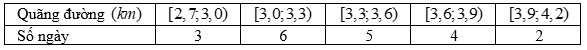Kiểm lâm thực hiện đo đường kính của một số cây thân gỗ tại hai khu vực A và B thu được kết quả như sau:
|
Đường kính (cm) |
[30; 32) |
[32; 34) |
[34; 36) |
[36; 38) |
[38; 40) |
|
A |
25 |
28 |
20 |
10 |
7 |
|
B |
22 |
27 |
19 |
18 |
14 |
Đường kính trung bình của cây tại hai khu vực A và B lần lượt là:
Ta có:
|
Đường kính (cm) |
[30; 32) |
[32; 34) |
[34; 36) |
[36; 38) |
[38; 40) |
|
Giá trị đại diện |
31 |
33 |
35 |
37 |
39 |
|
A |
25 |
28 |
20 |
10 |
7 |
|
B |
22 |
27 |
19 |
18 |
14 |
Suy ra