Hình trụ. Các công thức hình trụ

Hình trụ là một trong những khối hình quan trọng trong chương trình Hình học lớp 9. Nắm vững các công thức hình trụ sẽ giúp bạn dễ dàng giải quyết các bài toán tính diện tích, thể tích hình thực tế. Các bài toán đi kèm sẽ giúp bạn dễ dàng giải quyết các bài toán liên quan tính diện tích xung quanh và diện tích toàn phần. Bài viết dưới đây sẽ tổng hợp đầy đủ kiến ​​thức về hình trụ, kèm theo ví dụ minh họa cụ thể, giúp bạn học nhanh – nhớ lâu – làm bài chính xác.

A. Công thức hình trụ

Hình vẽ minh họa

B. Bài tập Hình trụ

Dạng 1: Tính chiều cao, bán kính đáy, diện tích xung quanh, diện tích toàn phần, thể tích

Bài 1. Điền đầy đủ các kết quả vào ô trống của bảng sau

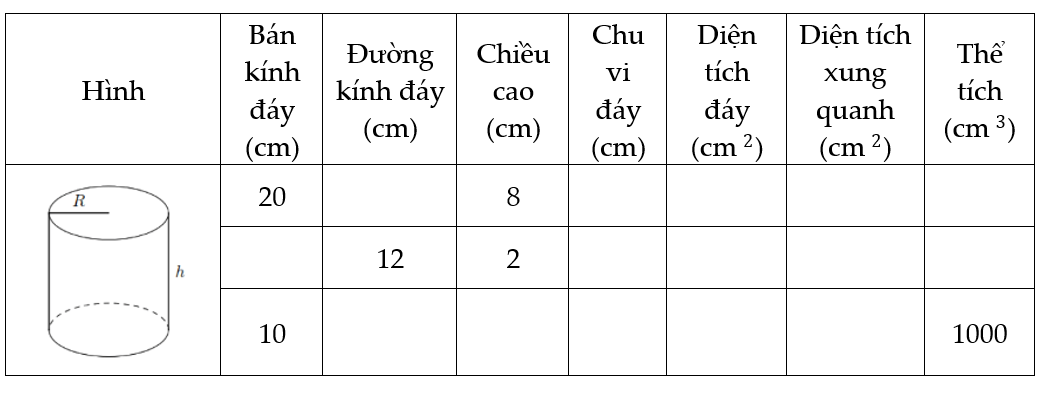
Hướng dẫn giải

Ta có

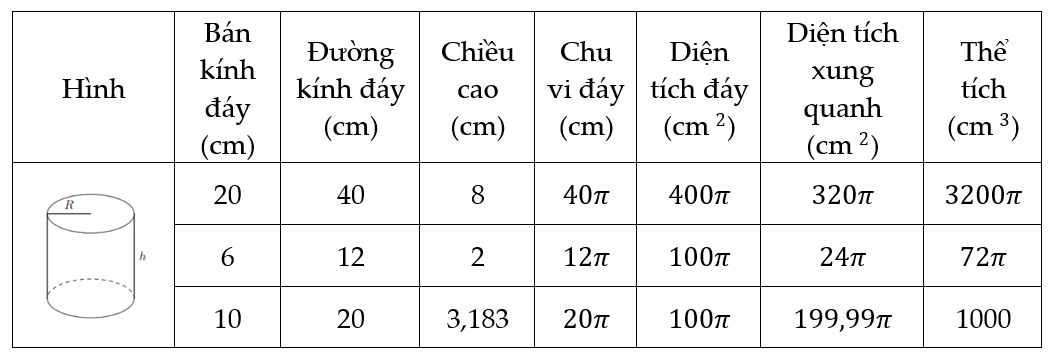
Bài 2. Một hình trụ có bán kính đáy đường tròn đáy là \(16\) cm, chiều cao là \(9\) cm. Tính

a) Diện tích xung quanh của hình trụ.

b) Thể tích của hình trụ. (Lấy \(\pi = 3,142\) làm tròn kết quả đến hàng đơn vị).

Hướng dẫn giải

a) Ta có \(S_{xq} = 2\pi Rl = 2 \cdot 3,142 \cdot 16 \cdot 9 = 983\ cm^{2}.\)

b) Ta có \(V = \pi R^{2}h = 3,142 \cdot 16^{2} \cdot 9 = 7239\ cm^{3}.\)

Bài 3. Cho hình chữ nhật \(ABCD\) có \(AB = 4,BC = 2\). Quay hình chữ nhật đó quanh \(AB\) thì được hình trụ có thể tích \(V_{1}\); quay quanh \(BC\) thì được hình trụ có thể tích \(V_{2}\). Trong các đẳng thức dưới đây đẳng thức nào đúng?

A. \(V_{1} = V_{2}\).                                   B. \(V_{1} = 2V_{2}\).

C. \(V_{2} = 2V_{1}\).                                 D. \(V_{2} = 3V_{1}\).

Hướng dẫn giải

Nhận thấy rằng:

Khi quay hình chữ nhật quanh \(AB\) thì

\(h = AB = 4\), \(R = BC = 2\) và \(V_{1} = \pi R^{2}h = \pi \cdot 2^{2} \cdot 4 = 16\pi\).

Khi quay hình chữ nhật quanh \(BC\) thì

\(h = BC = 2\), \(R = AB = 4\) và \(V_{2} = \pi R^{2}h = \pi \cdot 4^{2} \cdot 2 = 32\pi\).

Suy ra \(V_{2} = 2V_{1}.\)

Dạng 2: Kết hợp các kiến thức hình học

Bài 1. Một vật thể hình học có hình vẽ như hình bên. Phần trên là một nửa hình trụ, phần dưới là một hình hộp chữ nhật. Với các kích thước cho như hình vẽ.

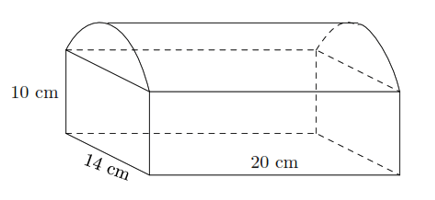
Thể tích của vật thể hình học này là:

A. \(4340\) cm\(^{3}\).                            B. \(4760\) cm\(\ ^{3}\).

C. \(5880\) cm\(^{3}\).                            D. \(8\) cm\(\ ^{3}\).

Hướng dẫn giải

Thể tích của hình hộp chữ nhật là \(V_{1} = 14 \cdot 20 \cdot 10 = 2800\ cm^{3}.\)

Thể tích nữa hình trụ là \(V_{2} = \frac{1}{2} \cdot 7^{2} \cdot \frac{22}{7} \cdot 20 = 1540\ cm^{3}.\)

Thể tích của vật thể là \(V = V_{1} + V_{2} = 4340\ cm^{3}.\)

Bài 2. Một hình trụ có bán kính đáy là \(3\) cm, chiều cao \(4\) cm được đặt đứng trên mặt bàn. Một phần của hình trụ bị cắt rời theo các bán kính \(OA\), \(OB\) và theo chiều dài thẳng đứng từ trên xuống dưới với \(\widehat{AOB} = 30^{0}\).

a) Tính thể tích của phần bị cắt.

b) Tính thể tích của phần còn lại.

c) Diện tích toàn phần của hình trụ sau khi đã bị cắt.

Hướng dẫn giải

Hình vẽ minh họa

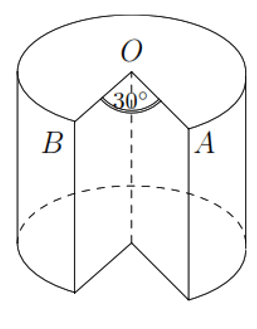
a) Ta có \(V_{1} = S_{q} \cdot h = \frac{\pi \cdot 3^{2} \cdot 30}{360} \cdot 4 = 3\pi\ cm^{3}.\)

b) Ta thấy \(V_{2} = V - V_{1} = \pi \cdot 3^{2} \cdot 4 - 3\pi = 33\pi\ cm^{3}.\)

c) Diện tích phần còn lại của hai đáy là \(2\left( \pi \cdot 9 - \frac{\pi \cdot 9 \cdot 30}{360} \right) = \frac{33}{2}\pi\ cm^{2}.\)

Diện tích xung quanh là \(2\pi Rh \cdot \frac{\pi R \cdot 30}{180} + 2Rh = 22\pi + 24\ cm^{2}.\)

Diện tích toàn phần là \(\frac{33}{2}\pi + 22\pi + 24 = 38\frac{1}{2}\pi + 24\ cm^{2}.\)

C. Bài tập tự rèn luyện

Bài 1. Điền đầy đủ các kết quả vào bảng sau:

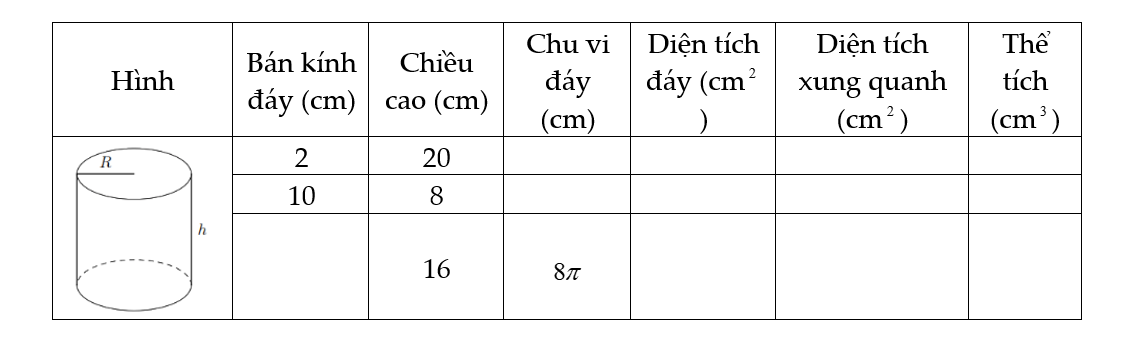
Bài 2. Một hình trụ có bán kính đáy là \(13\) cm, diện tích xung quanh bằng \(527\) cm\(\ ^{2}\). Khi đó, chiều cao của hình trụ là

A. \(27,958\) cm.            B. \(17,958\) cm.              C. \(6,451\) cm.                 D. \(28,958\) cm.

Bài 3. Chiều cao của một hình trụ bằng bán kính của đường tròn đáy. Diện tích xung quanh của hình trụ là \(314\) cm\(\ ^{2}\). Tính

a) Bán kính của đường tròn đáy.

b) Thể tích của khối trụ. (Làm tròn kết quả đến chữ số thập phân thứ hai).

Bài 4. Một cái trụ lăn có dạng hình trụ như hình bên.

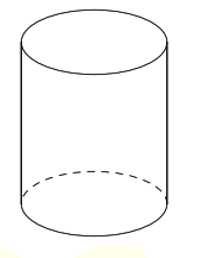
Đường kính của đường tròn đáy là \(42\) cm, chiều dài trục lăn là \(2\) m. Sau khi lăn trọn \(10\) vòng thì trụ lăn tạo trên mặt sân mặt phẳng một diện tích là \(\left( \pi = \frac{22}{7} \right)\).

A. \(24600\) cm\(\ ^{2}\).                               B. \(58200\) cm\(\ ^{2}\).

C. \(528\) m\(\ ^{2}\).                                     D. \(264000\) cm\(\ ^{2}\).

Bài 5. Một vật thể có thể dáng hình trụ, bán kính đường tròn đáy và độ dài của nó đều bằng \(2r\) (cm). Người ta khoan một lỗ cũng có dạng hình trụ như hình vẽ có bán kính đáy và độ sâu đều bằng \(r\) (cm). Thể tích phần vật thể còn lại tính theo cm\(\ ^{3}\) là

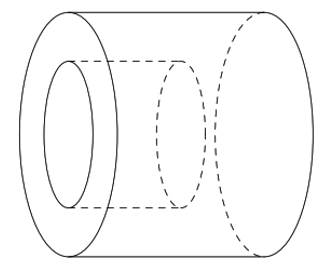
A. \(4\pi r^{3}\).                        B. \(7\pi r^{3}\).                  C. \(8\pi r^{3}\).                       D. \(9\pi r^{3}\).

Bải 6. Cho hình vẽ là một mẫu pho mát được cắt ra từ một khối pho mát dạng hình trụ (có các kích thước như hình sau).

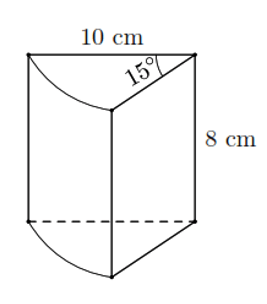
Khối lượng của mẫu pho mát là (khối lượng riêng của pho mát là \(3\) g/cm\(\ ^{3}\)).

A. \(100\) g.             B. \(100\pi\) g.                      C. \(800\) g.                          D. \(800\pi\) g.

----------------------------------

Hy vọng bài viết đã giúp bạn hiểu rõ hơn về hình trụ và các công thức hình trụ trong chương trình Toán học 9. Việc ghi nhớ công thức và luyện tập thường xuyên là chìa khóa giúp bạn làm tốt các dạng bài học không gian. Hãy chia sẻ nếu bạn thấy nội dung hữu ích và tiếp tục theo dõi các bài học bổ ích khác nhé!